Licencia
Copyright © 2018 Allen Downey, Ben Lauwens. Todos los derechos reservados.
Este libro está disponible bajo la Licencia Creative Commons Atribución-NoComercial 3.0 No portada. Es una traducción de ThinkJulia, el cual tiene la misma licencia. Una lista de las diferencias entre ThinkJulia y este libro está disponible en el Apéndice C.
Un PDF de este libro está disponible aquí.
Ben Lauwens es profesor de matemáticas en Royal Military Academy (RMA Bélgica). Tiene un doctorado en ingeniería y maestrías de KU Leuven y RMA, además de una licenciatura de RMA.
Allen Downey es profesor de informática en Olin College of Engineering. Ha dado clases en Wellesley College, Colby College y U.C. Berkeley. Tiene un doctorado en informática de U.C. Berkeley, y maestrías y licenciaturas del MIT.
Dedicatoria
Para Emeline, Arnaud y Tibo.
Prefacio
En enero de 2018 comencé a preparar un curso de programación pensado para estudiantes que no tuvieran experiencia previa en programación. Quería usar Julia como lenguaje de programación, y descubrí que no existía ningún libro para aprender a programar que usara Julia como primer lenguaje de programación. Hay tutoriales maravillosos que explican los conceptos clave de Julia, pero ninguno de ellos se dedicaba lo suficiente a enseñar a pensar como programador.
Conocía el libro Think Python de Allen Downey, el cual contiene todos los elementos clave para aprender a programar correctamente. Sin embargo, este libro se basa en el lenguaje de programación Python. Mi primer borrador del curso fue una mezcla de muchas referencias, pero a medida que trabajaba en este, el contenido comenzó a parecerse cada vez más a los capítulos de Think Python. Pronto, la idea de desarrollar mi curso como base para trasladar ese libro a Julia se hizo realidad.
Todo el material estaba disponible en un repositorio de GitHub, en forma de notebooks de Jupyter. Después de publicar un mensaje en el sitio Discourse de Julia sobre el progreso de mi curso, los comentarios fueron abrumadores. Aparentemente, un libro sobre conceptos básicos de programación con Julia como primer lenguaje de programación era algo que faltaba en el universo de Julia. Contacté a Allen para ver si podía iniciar oficialmente la versión de Think Python para Julia y su respuesta fue inmediata: “¡adelante!”, me puso en contacto con su editor de O’Reilly Media y ahora, un año después, estoy haciendo los retoques finales a este libro.
Fue un camino difícil. En Agosto de 2018 se lanzó Julia v1.0, y como todos mis colegas programadores de Julia, tuve que hacer una migración del código. Todos los ejemplos en el libro se prueban durante la conversión de los archivos fuente a archivos ASCIIDoc compatibles con O’Reilly. Tanto la cadena de herramientas como el código de los ejemplos tenían que ser compatibles con Julia v1.0. Afortunadamente no hay cursos en Agosto…
Espero que disfrutes al trabajar con este libro, y que te ayude a aprender a programar y pensar como informático, al menos un poco.
Ben Lauwens
¿Por qué Julia?
Julia fue lanzado originalmente en 2012 por Alan Edelman, Stefan Karpinski, Jeff Bezanson y Viral Shah. Es un lenguaje de programación gratuito y de código abierto.
La elección de un lenguaje de programación es siempre subjetiva. Para mí, las siguientes características de Julia son decisivas:
-
Julia está desarrollado como un lenguaje de programación de alto rendimiento.
-
Julia usa envío múltiple (“multiple dispatch” en inglés), que le permite al programador elegir entre diferentes patrones de programación de acuerdo a la aplicación.
-
Julia es un lenguaje de tipo dinámico que se puede usar fácilmente de forma interactiva.
-
Julia tiene una sintaxis de alto nivel que es fácil de aprender.
-
Julia es un lenguaje de programación con tipos opcionales, cuyos tipos de datos (definidos por el usuario) hacen que el código sea claro y robusto.
-
Julia tiene una biblioteca estándar extendida, además, están disponibles numerosos paquetes de terceros.
Julia es un lenguaje de programación único, ya que resuelve el problema de los dos idiomas. No se necesita de ningún otro lenguaje de programación para escribir código de alto rendimiento. Esto no significa que ocurra automáticamente. Es responsabilidad del programador optimizar el código que genere cuellos de botella, aunque esto puede hacerse directamente en Julia.
¿A quién está dirigido este libro?
Este libro es para cualquier persona que quiera aprender a programar. No se requieren conocimientos formales previos.
Los nuevos conceptos se introducen gradualmente, y los temas más avanzados se describen en capítulos posteriores.
Introducción a Julia puede ser usado como un curso de un semestre de nivel secundario o universitario.
Convenciones utilizadas en este libro
En este libro se siguen las siguientes convenciones tipográficas:
- Cursiva
-
Indica nuevos términos, URL, direcciones de correo electrónico, nombres de archivo y extensiones de archivo.
Ancho constante-
Se utiliza para mostrar código de programas, así como dentro de los párrafos para referirse a elementos del programa, como nombres de variables o funciones, bases de datos, tipos de datos, variables de entorno, sentencias y palabras reservadas.
Ancho constante en negrita-
Muestra comandos u otro texto que el usuario debe escribir.
Ancho constante en cursiva-
Muestra el texto que debe reemplazarse con valores proporcionados por el usuario o por valores determinados por el contexto.
|
Observación
|
Esto indica consejo o sugerencia. |
|
Nota
|
Esto es una nota general. |
|
Aviso
|
Esto indica una advertencia o precaución. |
Usando los códigos de ejemplo
Todo el código utilizado en este libro está disponible en un repositorio de Git en GitHub: https://github.com/JuliaIntro/IntroAJulia.jl. Si no está familiarizado con Git, es un sistema de control de versiones que le permite realizar seguimiento a los archivos que componen un proyecto. Una colección de archivos controlados por Git se denomina “repositorio”. GitHub es un servicio de hosting que proporciona almacenamiento para repositorios de Git, y una interfaz web conveniente.
El siguiente paquete puede ser de utilidad, y se puede agregar directamente a Julia. Simplemente escriba add https://github.com/JuliaIntro/IntroAJulia.jl en el REPL, en modo Pkg.
La forma más fácil de ejecutar un código de Julia es yendo a https://juliabox.com, e iniciar una sesión de prueba gratuita. Es posible utilizar tanto las interfaces REPL como de notebooks. Si desea tener Julia instalada localmente en su computadora, puede descargar JuliaPro de Julia Computing gratuitamente. Consiste en una versión reciente de Julia, el IDE de Juno basado en Atom y varios paquetes de Julia preinstalados. Si es más aventurero, puede descargar Julia desde https://julialang.org, instale el editor que prefiera, por ejemplo Atom o Visual Studio Code, activando los complementos para su integración de Julia. En el caso de una instalación local, también puede agregar el paquete IJulia que le permite ejecutar un notebook de Jupyter en su computadora.
Agradecimientos
Realmente quiero agradecer a Allen por escribir Think Python, y permitirme trasladar este libro a Julia. ¡Tu entusiasmo es contagioso!
También me gustaría agradecer a los revisores técnicos de este libro, que hicieron muchas sugerencias útiles: Tim Besard, Bart Janssens y David P. Sanders.
Gracias a Melissa Potter de O’Reilly Media por hacer de este un mejor libro. Me obligaste a hacer las cosas bien, y hacer que este libro sea lo más original posible.
Gracias a Matt Hacker de O’Reilly Media que me ayudó con la cadena de herramientas Atlas, y algunos problemas al destacar la sintaxis.
Gracias a todos los estudiantes que trabajaron con una versión temprana de este libro, y a todos los colaboradores (enumerados a continuación) que enviaron correcciones y sugerencias.
Lista de Colaboradores
Si tiene una sugerencia o corrección, abra un issue en GitHub. Si se realiza un cambio basado en sus comentarios, será agregado a la lista de contribuyentes (a menos que solicite ser omitido).
Avísenos con qué versión del libro está trabajando, y en qué formato. Si incluye al menos parte de la oración en la que aparece el error, eso facilita la búsqueda. Los números de página y sección también son útiles, pero no es tan fácil trabajar con ellos. ¡Gracias!
-
Scott Jones señaló el cambio de nombre de
VoidaNothingy con esto se comenzó la migración a Julia v1.0 -
Robin Deits encontró algunos errores tipográficos en el Capítulo 2.
-
Mark Schmitz sugirió destacar la sintaxis.
-
Zigu Zhao encontró algunos errores en el Capítulo 8.
-
Oleg Soloviev detectó un error en la url al agregar el paquete
ThinkJulia. -
Aaron Ang encontró algunos problemas de representación y nomenclatura.
-
Sergey Volkov encontró un enlace caído en el Capítulo 7.
-
Sean McAllister sugirió mencionar el excelente paquete
BenchmarkTools. -
Carlos Bolech envió una larga lista de correcciones y sugerencias.
-
Krishna Kumar corrigió el ejemplo de Markov en el Capítulo 18.
1. El camino de la programación
El objetivo de este libro es enseñarle a pensar como un informático. Esta manera de pensar combina las mejores características de las matemáticas, la ingeniería y las ciencias naturales. Los informáticos, al igual que los matemáticos, usan lenguajes formales para expresar ideas (específicamente cálculos). De manera similar a los ingenieros, diseñan estructuras, ensamblan componentes para formar sistemas, evaluando los costos y beneficios entre las alternativas. Además, observan el comportamiento de sistemas complejos, elaboran hipótesis y prueban predicciones, como los científicos.
La habilidad más importante para un informático es la resolución de problemas. Esto implica ser capaz de formular problemas, encontrar soluciones creativas, expresando una solución de forma clara y precisa. Como resultado, el proceso de aprender a programar es una excelente oportunidad para practicar habilidades de resolución de problemas. Es por ello que este capítulo se llama "El camino de la programación".
Por una parte, aprenderá a programar, que es una habilidad muy útil por sí misma. Pero, además, la programación se constituirá como un medio para un fin. A medida que avancemos, este fin será más claro.
¿Qué es un programa?
Un programa es una secuencia de instrucciones que especifica cómo hacer un cálculo. El cálculo puede ser de naturaleza matemática, tal como resolver un sistema de ecuaciones o encontrar las raíces de un polinomio, pero también puede ser un cálculo simbólico, como buscar y reemplazar texto en un documento, o bien algo gráfico, tal como procesar una imagen o reproducir un video.
Los detalles difieren para cada lenguaje, pero algunas instrucciones básicas aparecen en casi todos los lenguajes:
- Entrada/Input
-
Se obtienen datos a través del teclado, un archivo, una red u otro dispositivo.
- Salida/Output
-
Los datos se muestran por pantalla, se guardan en un archivo, se envían a través de la red, etc.
- Matemáticas
-
Se realizan operaciones matemáticas básicas como la suma y la multiplicación.
- Ejecución condicional
-
Se verifican ciertas condiciones y se ejecuta el código apropiado.
- Repetición
-
Se realiza alguna acción repetidamente, generalmente con alguna variación.
Aunque no lo crea, eso es todo lo que se debe hacer. Cada programa que ha usado, sin importar su complejidad, está construido basándose en instrucciones que se asemejan a estas. De esta manera, la programación puede entenderse como el proceso de dividir una tarea compleja y larga, en pequeñas subtareas lo suficientemente simples como para realizarse con una de estas instrucciones básicas.
Ejecutando Julia
Uno de los desafíos al comenzar a utilizar Julia es su instalación, además del software relacionado. Si está familiarizado con su sistema operativo y se siente cómodo con la interfaz de línea de comandos, no tendrá problemas. No obstante, para los principiantes puede ser difícil aprender sobre administración de sistema y programación al mismo tiempo.
Para evitar ese problema, se recomienda que comience ejecutando Julia en un navegador. Más tarde, cuando se sienta cómodo con Julia, se harán sugerencias para instalar Julia en su ordenador.
En el navegador, puede ejecutar Julia en JuliaBox. No se requiere instalación: simplemente abra su navegador y entre a la página de JuliaBox, inicie sesión y comience a programar (consulte Apéndice B).
Julia REPL (de "Read–Eval–Print Loop" que se traduce en "Bucle de Leer-Evaluar-Imprimir") es un programa que lee y ejecuta código de Julia. Puede iniciar REPL abriendo un terminal en JuliaBox y escribiendo julia en la línea de comando. Cuando comienza, debería ver una salida como esta:
_ _ _ _(_)_ | Documentation: https://docs.julialang.org (_) | (_) (_) | _ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help. | | | | | | |/ _` | | | | |_| | | | (_| | | Version 1.5.2 (2020-09-23) _/ |\__'_|_|_|\__'_| | Official https://julialang.org/ release |__/ | julia>
Las primeras líneas contienen información sobre el REPL, por lo que esto puede mostrarse diferente en su computadora. Debe verificar que la versión sea al menos 1.0.0.
El última línea es un indicador, señalando que el REPL está listo para que se ingrese una instrucción. Si escribe una línea de código y presiona Enter, la REPL muestra el resultado:
julia> 1 + 1
2Los fragmentos de código se pueden copiar y pegar textualmente, incluido el indicador julia> y cualquier salida.
Ahora ya está listo para comenzar. De aquí en adelante, ya sabrá cómo iniciar la REPL de Julia, y ejecutar su código.
El primer programa
Tradicionalmente, el primer programa que se escribe en un nuevo lenguaje se llama “¡Hola, mundo!”, porque todo lo que hace es mostrar las palabras “¡Hola, mundo!”. En Julia, se ve así:
julia> println("¡Hola, mundo!")
¡Hola, mundo!Este es un ejemplo de una sentencia de impresión, aunque en realidad no imprime nada en papel. Muestra un resultado en la pantalla.
Las comillas en el programa marcan el principio y el final del texto que se mostrará, y no aparecerán en el resultado.
Los paréntesis indican que println es una función. Se estudiarán funciones en Capítulo 3.
Operadores aritméticos
Después de nuestro programa “¡Hola, mundo!”, el siguiente paso es la aritmética. Julia tiene operadores, los cuales son símbolos que representan cálculos como la suma y la multiplicación.
Los operadores +, -, y * realizan las operaciones de suma, resta y multiplicación respectivamente, como se muestra en los siguientes ejemplos:
julia> 40 + 2
42
julia> 43 - 1
42
julia> 6 * 7
42El operador / realiza la división:
julia> 84/2
42.0Quizás se pregunte por qué el resultado es 42.0 en vez de 42. Esto será explicado en la siguiente sección.
Finalmente, el operador ^ realiza la potencición, es decir, eleva un número a una potencia:
julia> 6^2 + 6
42Valores y tipos
Un valor es uno de los elementos básicos con los que trabaja un programa, tal como una letra o un número. Algunos de los valores que hemos visto hasta ahora son 2, 42.0 y "Hola, Mundo!".
Estos valores pertenecen a diferentes tipos: 2 es un entero (integer en inglés), 42.0 es un número de punto flotante (floating-point number en inglés), y "Hola, Mundo!" es una cadena de caracteres (string en inglés), llamada así porque las letras que contiene están unidas.
Si no está seguro del tipo de un valor, el REPL puede ayudarle:
julia> typeof(2)
Int64
julia> typeof(42.0)
Float64
julia> typeof("¡Hola, mundo!")
StringLos enteros pertenecen al tipo Int64, las cadenas pertenecen a String y los números de punto flotante pertenecen a Float64.
¿Qué pasa con los valores "2" y "42.0"? Parecen números, pero están entre comillas como si fueran cadenas. Estos valores también son cadenas:
julia> typeof("2")
String
julia> typeof("42.0")
StringSi se quiere escribir un número de grandes dimensiones, se podría caer en la costumbre de usar comas para separar sus cifras, como por ejemplo 1,000,000. Este no es un entero válido en Julia, aunque sí es válido.
julia> 1,000,000
(1, 0, 0)¡Esto no es lo que se podría esperar! Julia entiende 1,000,000 como una secuencia de enteros separados por comas. Más adelante aprenderemos más sobre este tipo de secuencias.
Sin embargo, puede obtener el resultado esperado usando 1_000_000.
Lenguajes formales y naturales
Los lenguajes naturales son los lenguajes hablados, como el español, el inglés o el francés, no fueron diseñados por personas (aunque las personas intentan imponerles un orden); sino que evolucionaron naturalmente.
Los lenguajes formales son lenguajes diseñados por personas para propósitos específicos. Por ejemplo, la notación que usan los matemáticos es un lenguaje formal particularmente útil para denotar relaciones entre números y símbolos. Los químicos usan un lenguaje formal para representar la estructura química de las moléculas. Los lenguajes de programación también son lenguajes formales y han sido diseñados para expresar cálculos.
Los lenguajes formales tienden a dictar reglas estrictas de sintaxis que gobiernan la estructura de las sentencias. Por ejemplo, en matemáticas, la sentencia \(3 + 3 = 6\) tiene la sintaxis correcta, pero \(3 += 3 \$ 6\) no. En química, \(\Large{H_2O}\) es una fórmula sintácticamente correcta, pero \(\Large{_2Zz}\) no lo es.
Las reglas de sintaxis pueden ser de dos tipos, correspondientes a componentes léxicos y a estructura. Los componentes léxicos son los elementos básicos del lenguaje, como palabras, números y elementos químicos. Uno de los problemas con \(3 += 3 \$ 6\) es que \(\$\) no es un componente léxico válido en matemáticas (al menos hasta donde conocemos). Del mismo modo, \(\Large{_2Zz}\) no es válido porque no existe ningún elemento con la abreviatura \(\Large{Zz}\).
El segundo tipo de reglas de sintaxis se refiere a la forma en que se combinan los componentes léxicos. La ecuación \(3 += 3 \) no es válida porque aunque \(+\) y \(=\) son componentes léxicos válidos, no se puede tener uno justo después el otro. Del mismo modo, en una fórmula química, el subíndice se coloca después del nombre del elemento, no antes.
Esta es un@ oración en espa$ol bien estructurada con c*mponentes léxicos no válidos. Esta oración léxicos todos componentes los tiene, pero estructura una no válida con.
Cuando se lee una oración en español, o en un lenguaje formal, se tiene que descubrir la estructura (aunque en un lenguaje natural se hace inconscientemente). Este proceso se llama parsing o análisis de sintaxis.
Aunque los lenguajes formales y naturales tienen muchas características en común—componentes léxicos, estructura y sintaxis—existen algunas diferencias:
- Ambigüedad
-
Los lenguajes naturales están llenos de ambigüedades, este problema es abordado mediante el uso del contexto y otra información. Los lenguajes formales están diseñados para ser casi completamente precisos, lo que significa que cualquier declaración tiene exactamente un significado, independientemente del contexto.
- Redundancia
-
Para compensar la ambigüedad y reducir los malentendidos, los lenguajes naturales emplean mucha redundancia. Como resultado, a menudo son verbosos. Los lenguajes formales son menos redundantes y más concisos.
- Metáfora
-
Los lenguajes naturales están llenos de modismos y metáforas. Si se dice: “Caí en la cuenta”", probablemente no haya una cuenta, y nada que se caiga (este modismo significa que alguien entendió algo después de un período de confusión). Por otro lado, los lenguajes formales significan exactamente lo que expresan.
Debido a que todo el mundo crece hablando lenguajes naturales, a veces es difícil adaptarse a los lenguajes formales. La diferencia entre lenguaje formal y natural es como la diferencia entre la poesía y la prosa:
- Poesía
-
Las palabras se usan por sus sonidos y significados. El poema en conjunto crea un efecto o una respuesta emocional. La ambigüedad no sólo es común sino a menudo, deliberada.
- Prosa
-
El significado literal de las palabras es más importante, y la estructura aporta significado. La prosa es más fácil de analizar que la poesía, pero a menudo sigue siendo ambigua.
- Programas
-
El significado de un programa computacional es inequívoco y literal, y puede entenderse por completo mediante el análisis de los componentes léxicos y de estructura.
Los lenguajes formales son más densos que los naturales, por lo que lleva más tiempo leerlos. Además, la estructura es importante, por lo que no siempre es mejor leer de arriba a abajo, y de izquierda a derecha. En cambio, aprenderá a analizar el programa mentalmente, identificando los componentes léxicos e interpretando la estructura. Finalmente, los detalles son importantes. Pequeños errores de ortografía y puntuación, que pueden pasar desapercibidos en los lenguajes naturales, pueden hacer una gran diferencia en un lenguaje formal.
Depuración
Los programadores cometen errores. Los errores de programación se denominan bugs y el proceso para rastrearlos se denomina debugging o depuración.
La programación, y especialmente la depuración, pueden provocar emociones negativas. Frente a un error difícil de solucionar, puede sentir enojo, vergüenza, ó cansancio.
Existe evidencia de que las personas responden naturalmente a las computadoras como si fueran personas. Cuando trabajan bien, se los considera compañeros de equipo, y cuando son obstinados o groseros, se los trata de la misma manera que a personas groseras y obstinadas. [1]
Prepararse para estas reacciones puede ayudarlo a lidiar con ellas. Un enfoque es pensar en la computadora como un empleado con ciertas fortalezas, como la velocidad y la precisión, y debilidades particulares, como la falta de empatía y la incapacidad para comprender el panorama general.
Su trabajo es ser un buen gerente: debe encontrar formas de aprovechar las fortalezas y mitigar las debilidades. Además, debe encontrar formas de usar sus emociones para involucrarse con el problema, sin dejar que sus reacciones interfieran con su capacidad para trabajar de manera efectiva.
Aprender a depurar puede ser frustrante, pero es una habilidad valiosa que es útil para muchas actividades más allá de la programación. Al final de cada capítulo hay una sección, como esta, con algunas sugerencias para la depuración. ¡Espero que le sean de ayuda!
Glosario
- resolución de problemas
-
El proceso de formular un problema, encontrar una solución y expresarla.
- programa
-
Una secuencia de instrucciones que especifica un cálculo.
- REPL
-
Un programa, que de manera reiterada lee una entrada, la ejecuta y genera resultados.
- indicador
-
Caracteres mostrados por el REPL para indicar que está listo para recibir información de entrada de parte del usuario.
- sentencia de impresión (print)
-
Una instrucción que hace que el REPL de Julia muestre un valor en la pantalla.
- operador
-
Un símbolo que representa un cálculo simple como la suma, la multiplicación o la concatenación de cadenas.
- valor
-
Una de las unidades básicas de datos, como un número o cadena, que manipula un programa.
- tipo
-
Una categoría de valores . Los tipos que se han visto hasta ahora son enteros (
Int64), números de punto flotante (Float64) y cadenas (String). - entero
-
Un tipo que representa números enteros.
- punto flotante
-
Un tipo que representa números con un punto decimal.
- cadena
-
Un tipo que representa secuencias de caracteres.
- lenguaje natural
-
Cualquier lenguaje hablado que evoluciona naturalmente.
- lenguaje formal
-
Cualquier lenguaje diseñado para fines específicos, como la representación de ideas matemáticas o programas de computadora. Todos los lenguajes de programación son lenguajes formales.
- sintaxis
-
Las reglas que gobiernan la estructura de un programa.
- componente léxico
-
Uno de los elementos básicos de la estructura de un programa, análogo a una palabra en un lenguaje natural.
- estructura
-
La manera en que los componentes léxicos se combinan.
- análisis de sintaxis
-
Examinar un programa y analizar la estructura sintáctica.
- bug
-
Un error en un programa.
- depuración/debugging
-
El proceso de búsqueda y corrección de errores.
Ejercicios
|
Observación
|
Es una buena idea leer este libro frente a una computadora, para hacer los ejemplos y ejercicios conforme avance. |
Ejercicio 1-1
Siempre que esté experimentando con algo nuevo, debe intentar cometer errores. Por ejemplo, en el programa “¡Hola, mundo!”, ¿Qué sucede si omite una de las comillas? ¿Qué pasa si omite ambas? ¿Qué ocurre si escribe mal println?
Este tipo de ejercicios le ayuda a recordar lo que leyó; también le ayuda a programar, porque puede saber qué significan los mensajes de error. Es mejor cometer errores ahora y a propósito, en lugar de después y accidentalmente.
-
En un comando print, ¿Qué sucede si omite uno de los paréntesis, o ambos?
-
Si está intentando imprimir un string, ¿Qué sucede si omite una de las comillas o ambas?
-
Se puede usar un signo menos para escribir un número negativo, como
-2. ¿Qué sucede si pone un signo + antes de un número? ¿Qué pasa con2++2? -
En notación matemática, los ceros a la izquierda son correctos, como en
02. ¿Qué pasa si intenta esto en Julia? -
¿Qué sucede si tiene dos valores sin operador entre ellos?
Ejercicio 1-2
Inicie el REPL de Julia, y úselo como una calculadora.
-
¿Cuántos segundos hay en 42 minutos y 42 segundos?
-
¿Cuántas millas hay en 10 kilómetros?
ObservaciónHay 1.61 kilómetros en una milla.
-
Si corre una carrera de 10 kilómetros en 37 minutos y 48 segundos, ¿Cuál es su ritmo promedio (tiempo por milla en minutos y segundos)? ¿Cuál es su velocidad promedio en millas por hora?
2. Variables, expresiones y sentencias
Una de las características más poderosas de un lenguaje de programación es la capacidad de manipular variables. Una variable es un nombre que hace referencia a un valor.
Sentencias de asignación
Una sentencia de asignación crea una nueva variable y le asigna un valor:
julia> mensaje = "Y ahora, algo completamente diferente"
"Y ahora, algo completamente diferente"
julia> n = 17
17
julia> π_val = 3.141592653589793
3.141592653589793Este ejemplo realiza tres asignaciones. La primera asigna una cadena a una nueva variable llamada mensaje; la segunda le asigna el entero 17 a la variable n; la tercera asigna el valor (aproximado) de π (\pi TAB) a la variable π_val.
Una forma común de representar variables en papel es escribir el nombre de la variable con una flecha apuntando a su valor. Este tipo de figura se llama “diagrama de estado” porque muestra en qué estado se encuentra cada una de las variables. La Figura 1, Figura 1, muestra el resultado del ejemplo anterior.
Nombres de variables
Los programadores generalmente eligen nombres representativos para sus variables, es decir, nombres que explican para qué se usa o qué contiene la variable.
Los nombres de las variables pueden ser tan largos como se desee. Pueden contener casi todos los caracteres Unicode (consulte Sección 8.1), pero no pueden comenzar con un número. Es válido usar letras mayúsculas, pero lo común es usar solo minúsculas para nombres de variables.
Los caracteres Unicode se pueden ingresar mediante autocompletado por tabulación de las abreviaturas tipo LaTeX en el REPL de Julia.
El carácter guión bajo, _, puede formar parte del nombre de una variable. Generalmente se usa como separador en nombres con varias palabras, como por ejemplo en tu_nombre o velocidad_aerodinamica_de_una_golondrina_sin_cargamento.
Si se le da un nombre inválido a una variable, aparece un error de sintaxis:
julia> 76trombones = "un gran desfile"
ERROR: syntax: "76" is not a valid function argument name (ERROR: sintaxis: "76" no es un nombre de argumento de función válido)
julia> mas@ = 1000000
ERROR: syntax: extra token "@" after end of expression (ERROR: sintaxis: componente léxico adicional "@" después del final de la expresión)
julia> struct = "Química avanzada"
ERROR: syntax: unexpected "=" (ERROR: sintaxis: "=" inesperado)76trombones es un nombre de variable inválido porque comienza con un número. También es inválido mas@ porque contiene el carácter inválido: @. Pero, ¿Cuál es el error en struct?
Resulta que struct es una de las palabras reservadas de Julia. Julia usa las palabras reservadas para reconocer la estructura del programa, por ello no pueden usarse como nombres de variables.
Julia tiene las siguientes palabras reservadas:
abstract type baremodule begin break catch const continue do else elseif end export finally for function global if import importall in let local macro module mutable struct primitive type quote return try using struct where while
No es necesario memorizar esta lista. En la mayoría de los entornos de desarrollo, las palabras reservadas se muestran en un color diferente; por lo tanto, si intenta usar una como nombre de variable, lo sabrá.
Expresiones y sentencias
Una expresión es una combinación de valores, variables y operadores. Un valor o una variable por sí solos se consideran una expresión, por lo que las siguientes expresiones son válidas:
julia> 42
42
julia> n
17
julia> n + 25
42Cuando escribe una expresión en el indicador, el REPL la evalúa, lo que significa que encuentra el valor de la expresión. En este ejemplo, n tiene el valor 17 previamente asignado y n+25 retorna el valor 42.
Una sentencia es una unidad de código que tiene un efecto, tal como crear una variable o mostrar un valor.
julia> n = 17
17
julia> println(n)
17La primera línea es una sentencia de asignación, ya que asigna un valor a n. La segunda línea es una sentencia de impresión que muestra el valor de n.
Cuando escribe una sentencia, REPL la ejecuta, es decir, hace lo que dice la sentencia.
Modo script
Hasta ahora se ha ejecutado Julia en modo interactivo, lo que significa que se ha interactuado directamente con el REPL. Este modo es una buena manera de comenzar, pero si está trabajando con varias líneas de código, puede resultar incómodo.
Una alternativa es guardar el código en un archivo de órdenes o script y luego utilizar Julia en modo script para ejecutarlo. Por convención, los scripts de Julia tienen nombres que terminan con la extensión .jl.
Si sabe cómo crear y ejecutar un script en su computadora, está listo para comenzar. De lo contrario, es recomendable usar JuliaBox nuevamente. Abra un archivo de texto, escriba el script y guárdelo con la extensión .jl. El script se puede ejecutar en una terminal con el comando julia nombre_del_script.jl.
Debido a que Julia proporciona ambos modos, puede probar líneas de código en modo interactivo antes de colocarlos en un script. Aún así, tenga en consideración que existen diferencias entre el modo interactivo y el modo script que pueden generar confusión.
Por ejemplo, si está utilizando Julia como una calculadora, puede escribir
julia> millas = 26.2
26.2
julia> millas * 1.61
42.182La primera línea asigna un valor a millas y muestra el valor. La segunda línea es una expresión, por lo que el REPL la evalúa y muestra el resultado. Gracias al código anterior sabemos que una maratón tiene unos 42 kilómetros.
Pero, si escribe el mismo código en un script y lo ejecuta, no obtendrá ningún resultado. En el modo script, una expresión, por sí sola, no tiene ningún efecto visible. Julia evalúa la expresión, pero no muestra el valor a menos que se lo indique:
millas = 26.2
println(millas * 1.61)Al principio este comportamiento puede ser confuso.
Un script generalmente contiene una secuencia de sentencias. Si hay más de una sentencia, los resultados aparecen de uno a la vez a medida que se ejecutan las sentencias.
Por ejemplo, el script
println(1)
x = 2
println(x)produce la salida
1
2Notar que la sentencia de asignación x = 2 no tiene salida.
Ejercicio 2-1
Para comprobar que ha comprendido lo recientemente explicado, escriba las siguientes sentencias en el REPL de Julia y vea lo que hace cada una:
5
x = 5
x + 1Ahora coloque las mismas sentencias en un script y ejecútelo. ¿Cuál es el resultado? Modifique el script transformando cada expresión en una sentencia de impresión y luego ejecútelo de nuevo.
Orden de operaciones
Cuando una expresión contiene más de un operador, el orden de evaluación depende de las reglas de precedencia. Julia sigue la convención matemática para el orden de evaluación de los operadores matemáticos. El acrónimo PAPOMUDAS es una forma útil de recordar estas reglas:
-
PAréntesis: tienen la mayor precedencia y se pueden utilizar para forzar la evaluación de una expresión en el orden que se desee. Dado que las expresiones entre paréntesis se evalúan primero,
2*(3-1)es4, y(1+1)^(5-2)es8. También puede usar paréntesis para hacer una expresión más fácil de leer, como en(minuto*100)/60, incluso si no cambia el resultado. -
POtenciación: tiene la siguiente precedencia más alta, por lo que
1+2^3es9, no27, y2*3^2es18, no36. -
MUltiplicación y División tienen mayor precedencia que la Adición y Sustracción. Entonces
2*3-1es5, no4, y6+4/2es8, no5. -
Los operadores con la misma precedencia se evalúan de izquierda a derecha (excepto potencias). Entonces, en la expresión
grados/2*π, la división ocurre primero y el resultado se multiplica porπ. Para dividir entre \(2\pi\), puede usar paréntesis, escribirgrados/2/πogrados/2π.
|
Observación
|
No se esfuerce demasiado en recordar el orden de las operaciones. Si el orden no es evidente mirando la expresión, use paréntesis para que sí lo sea. |
Operaciones con cadenas
En general, no se pueden realizar operaciones matemáticas con cadenas, aunque las cadenas puedan parecer números, por lo que lo siguiente es inválido:
"2" - "1"
"huevos" / "fácil"
"tercero" + "talismán"No obstante, hay dos excepciones, y ^.
El operador * realiza concatenación de cadenas, lo que significa que une las cadenas de extremo a extremo. Por ejemplo:
julia> primer_str = "auto"
"auto"
julia> segundo_str = "móvil"
"móvil"
julia> primer_str * segundo_str
"automóvil"El operador ^ también funciona con cadenas generando repeticiones. Por ejemplo, "Spam"^3 es "SpamSpamSpam". Si uno de los valores es una cadena, el otro tiene que ser un número entero.
De manera análoga, este uso de * y ^ también tiene sentido en la multiplicación y potencia. Así como 4^3 es equivalente a 4*4*4, esperamos que el "Spam"^3 sea lo mismo que el "Spam"*"Spam"*"Spam", y lo es.
Comentarios
A medida que los programas se hacen más largos y complejos, se vuelven más difíciles de leer. Los lenguajes formales son densos, y a menudo es difícil leer el código y entender qué está haciendo o por qué.
Por esta razón, es una buena idea agregar notas a sus programas para explicar en lenguaje natural lo que está haciendo el programa. Estas notas se llaman comentarios, y comienzan con el símbolo #:
# calcula el porcentaje de hora que ha transcurrido
porcentaje = (minuto * 100) / 60En este caso, el comentario aparece sólo en una línea. También puede poner comentarios al final de una línea:
porcentaje = (minuto * 100) / 60 # porcentaje de una horaTodo, desde el # hasta el final de la línea se ignora y no tiene ningún efecto en la ejecución del programa.
Los comentarios son más útiles cuando documentan características no obvias del código. Es razonable suponer que el lector puede averiguar qué hace el código, por lo tanto es más útil explicar por qué.
Este comentario es inútil porque es redundante con el código:
v = 5 # asigna 5 a vEste comentario contiene información útil que no está presente en el código:
v = 5 # velocidad en metros/segundo.|
Observación
|
Los nombres de las variables tienen que ser descriptivos para así reducir la necesidad de comentarios, pero no tan largos como para dificultar la lectura del código. |
Depuración
Se pueden producir tres tipos de errores en un programa: errores de sintaxis, errores en tiempo de ejecución, y errores semánticos. Es útil distinguirlos para rastrearlos más rápidamente.
- Error de sintaxis
-
“Sintaxis” se refiere a la estructura de un programa y las reglas sobre esa estructura. Por ejemplo, los paréntesis deben presentarse de a pares, por lo que
(1+2)es válido, pero8)es un error de sintaxis.Si hay un error de sintaxis en cualquier parte de su programa, Julia muestra un mensaje de error y se cierra, no pudiendo ejecutar el programa. Durante sus primeras semanas como programador, puede pasar mucho tiempo rastreando errores de sintaxis. A medida que gane experiencia, cometerá menos errores y los encontrará más rápido.
- Error en tiempo de ejecución
-
El segundo tipo de error es el error en tiempo de ejecución, llamado así porque aparece durante la ejecución del programa. Estos errores también se denominan excepciones porque generalmente indican que ha sucedido algo excepcional (y malo).
Los errores en tiempo de ejecución son raros en los programas simples que verá en los primeros capítulos, por lo que puede pasar un tiempo antes de que encuentre uno.
- Error semántico
-
El tercer tipo de error es “semántico”, es decir, relacionado con el significado. Si hay un error semántico en su programa, este se ejecutará sin generar mensajes de error, pero no hará lo que se desea, sino que hará otra cosa. Específicamente, hará lo que usted le dijo que hiciera, (y no lo que usted desea que realice).
Identificar errores semánticos puede ser complicado porque requiere que se trabaje a la inversa, analizando la salida del programa para intentar descubrir qué está haciendo.
Glosario
- variable
-
Un nombre que hace referencia a un valor.
- asignación
-
Una sentencia que asigna un valor a una variable.
- diagrama de estado
-
Una representación gráfica de un conjunto de variables y los valores a los que hace referencia.
- palabra clave
-
Una palabra reservada que se utiliza para definir la sintaxis y estructura de un programa; no puede usar palabras reservadas como
if,functionywhilecomo nombres de variables. - operando
-
Uno de los valores sobre los que opera un operador.
- expresión
-
Una combinación de variables, operadores y valores que representa un solo valor como resultado.
- evaluar
-
Simplificar una expresión realizando operaciones para obtener un solo valor.
- sentencia
-
Una sección de código que representa un comando o acción. Hasta ahora, las sentencias que hemos visto son asignaciones e impresiones.
- ejecutar
-
Ejecutar una sentencia y hacer lo que ésta dice.
- modo interactivo
-
Una forma de utilizar el REPL de Julia escribiendo código en el indicador.
- modo script
-
Una forma de usar Julia para leer código desde un script y ejecutarlo.
- script
-
Un programa almacenado en un archivo.
- precedencia del operador
-
Reglas que rigen el orden en que se evalúan las expresiones que involucran múltiples operadores matemáticos y operandos.
- concatenar
-
Unir dos cadenas de extremo a extremo.
- comentario
-
Información en un programa que está destinada a otros programadores (o cualquier persona que lea el código fuente) y que no tiene efecto en la ejecución del programa.
- error de sintaxis
-
Un error en un programa que hace que sea imposible de analizar (y, por lo tanto, imposible de ejecutar).
- error en tiempo de ejecución o excepción
-
Un error que se detecta mientras se ejecuta el programa.
- semántica
-
El significado de un programa.
- error semántico
-
Es un error en un programa, que provoca que se haga algo diferente a lo que el programador pretendía.
Ejercicios
Ejercicio 2-2
Repitiendo el consejo del capítulo anterior, cada vez que aprenda algo nuevo, debe probarlo en el modo interactivo y cometer errores a propósito para ver el resultado.
-
Hemos visto que
n=42es válido. ¿Qué pasa con42=n? -
¿Y con
x=y=1? -
En algunos lenguajes, cada sentencia termina con un punto y coma:
;. ¿Qué sucede si pone un punto y coma al final de una sentencia en Julia? -
¿Qué pasa si pone un punto al final de una sentencia?
-
En notación matemática puede multiplicar
xeyde esta manera:x y. ¿Qué pasa si intenta eso en Julia? ¿Y qué sucede con 5x?
Ejercicio 2-3
Practique usando el REPL de Julia como una calculadora:
-
El volumen de una esfera con radio \(r\) es \(\frac{4}{3} \pi r^3\). ¿Cuál es el volumen de una esfera con radio 5?
-
Supongamos que el precio de venta de un libro es de $24.95, pero las librerías obtienen un descuento del 40%. El envío cuesta $3 por la primera copia y 75 centavos por cada copia adicional. ¿Cuál es el costo total al por mayor de 60 copias?
-
Si una persona sale de casa a las 6:52 a.m. y corre 1 milla a un ritmo relajado (8:15 minutos por milla), luego 3 millas más rápido (7:12 minutos por milla) y 1 milla a ritmo relajado nuevamente, ¿A qué hora llega a casa para desayunar?
3. Funciones
En el contexto de la programación, una función es una secuencia de sentencias que ejecuta una operación deseada y tiene un nombre. Cuando se define una función, se especifica su nombre y secuencia de sentencias. Una vez hecho esto, se puede "llamar" a la función por su nombre.
Llamada a función
Ya se ha visto un ejemplo de una llamada a función:
julia> println("¡Hola, Mundo!")
¡Hola, Mundo!El nombre de esta función es println. La expresión entre paréntesis se llama argumento de la función.
Es común decir que una función "toma" un argumento y "devuelve" un resultado. El resultado también se llama valor de retorno.
Julia tiene funciones integradas que convierten valores de un tipo a otro. La función parse toma una cadena y, si es posible, la convierte en cualquier tipo de número, en caso contrario arroja error:
julia> parse(Int64, "32")
32
julia> parse(Float64, "3.14159")
3.14159
julia> parse(Int64, "Hola")
ERROR: ArgumentError: invalid base 10 digit 'H' in "Hola"(ERROR: ArgumentError: base inválida de 10 dígitos H en "Hola")
trunc puede convertir valores de punto flotante a enteros, pero no redondea; sino que trunca:
julia> trunc(Int64, 3.99999)
3
julia> trunc(Int64, -2.3)
-2float convierte números enteros en números de punto flotante:
julia> float(32)
32.0Finalmente, string convierte el argumento en una cadena:
julia> string(32)
"32"
julia> string(3.14159)
"3.14159"Funciones matemáticas
En Julia, la mayoría de las funciones matemáticas conocidas están disponibles directamente:
proporción = potencia_de_señal/potencia_de_ruido
decibelios = 10*log10(proporción)Este primer ejemplo utiliza la función log10 para calcular la proporción entre señal y ruido en decibelios (suponiendo que potencia_de_señal y potencia_de_ruido están definidos). También existe la función log, que calcula el logaritmo natural.
radianes = 0.7
altura = sin(radianes)Este segundo ejemplo encuentra la razón seno (en inglés sine) de la variable radianes. El nombre de esta variable es una pista de que la función sin y las otras funciones trigonométricas (cos, tan, etc.) toman argumentos en radianes. Para convertir grados a radianes, se debe dividir por 180 y multiplicar por \(\pi\):
julia> grados=45
45
julia> radianes=grados/180*π
0.7853981633974483
julia> sin(radianes)
0.7071067811865475El valor de la variable π es una aproximación de punto flotante de \(\pi \), con una precisión de aproximadamente 16 dígitos.
Si sabe de trigonometría, puede verificar el resultado anterior comparándolo con la raíz cuadrada de dos dividido por dos:
julia> sqrt(2)/ 2
0.7071067811865476Composición
Hasta ahora, hemos analizado los elementos de un programa (variables, expresiones y sentencias) de forma aislada, sin mencionar cómo se combinan.
Una de las características más útiles de los lenguajes de programación es su capacidad para combinar pequeños bloques de código. Por ejemplo, el argumento de una función puede ser cualquier tipo de expresión, incluidos operadores aritméticos:
x = sin(grados/360*2*π)E incluso llamadas a funciones:
x = exp(log(x + 1))Casi en cualquier lugar donde se pueda colocar un valor, se puede colocar una expresión arbitraria, con una excepción: el lado izquierdo de una sentencia de asignación debe ser un nombre de variable. Cualquier otra expresión en el lado izquierdo genera un error de sintaxis (se verán excepciones a esta regla más adelante).
2
julia> minutos = horas * 60 # bien
120
julia> horas * 60 = minutos # mal!
ERROR: syntax: "60" is not a valid function argument name(ERROR: sintaxis: "60" no es un nombre de argumento de función válido)
Agregar nuevas funciones
Hasta ahora, solo hemos usado las funciones integradas en Julia, pero también es posible agregar nuevas funciones. Una definición de función especifica el nombre de una nueva función y la secuencia de sentencias que se ejecutan cuando se llama a la función. A continuación se muestra un ejemplo:
function imprimirletras()
println("Juguemos en el bosque")
println("mientras el lobo no está.")
endfunction es una palabra reservada que indica que esta es una definición de función. El nombre de la función es imprimirletras. Las reglas para los nombres de funciones son las mismas que para los nombres de variables: pueden contener casi todos los caracteres Unicode (consulte Sección 8.1), pero el primer carácter no puede ser un número. No puede usar una palabra reservada como nombre de una función, y debe evitar tener una variable y una función con el mismo nombre.
Los paréntesis vacíos después del nombre indican que esta función no tiene argumentos.
La primera línea de una definición de función se llama encabezado; el resto se llama cuerpo. El cuerpo termina con la palabra reservada end y puede contener todas las sentencias que desee. Para facilitar la lectura, el cuerpo de la función debería tener sangría.
Las comillas deben ser "comillas rectas" (""), generalmente ubicadas junto a la tecla Enter en el teclado. Las "comillas inglesas" (“”)no son válidas en Julia.
Si escribe una definición de función en modo interactivo, Julia REPL inserta una sangría para informarle que la definición no está completa:
julia> function imprimirletras()
println("Juguemos en el bosque")Para finalizar la función, debe escribir end.
La sintaxis para llamar a la nueva función es la misma que para las funciones integradas en Julia:
julia> imprimirletras()
Juguemos en el bosque
mientras el lobo no está.Una vez definida una función, puede usarla dentro de otra función. Por ejemplo, para repetir el estribillo anterior, se podría escribir una función llamada repetirletras:
function repetirletras()
imprimirletras()
imprimirletras()
endY luego llamar a repetirletras:
julia> repetirletras()
Juguemos en el bosque
mientras el lobo no está.
Juguemos en el bosque
mientras el lobo no está.Definiciones y usos
Al unir los fragmentos de código de la sección anterior, todo el programa se ve así:
function imprimirletras()
println("Jueguemos en el bosque")
println("mientras el lobo no está.")
end
función repetirletras()
imprimirletras()
imprimirletras()
end
repetirletras()Este programa contiene dos definiciones de función: imprimirletras y repetirletras. Las definiciones de función se ejecutan al igual que otras sentencias, pero su ejecución crea nuevas funciones. Las sentencias dentro de la función no se ejecutan hasta que se llama a la función, y la definición de la función no genera salida.
Como es de esperar, debe crear una función antes de poder ejecutarla. En otras palabras, la definición de la función tiene que ejecutarse antes de que se llame a la función.
Ejercicio 3-1
Mueva la última línea de este programa a la parte superior, de modo que la llamada a función aparezca antes de las definiciones. Ejecute el programa y vea qué mensaje de error obtiene.
Ahora mueva la llamada a función hacia abajo y coloque la definición de imprimirletras después de la definición de repetirletras. ¿Qué sucede cuando ejecuta este programa?
Flujo de ejecución
Para asegurarse de que una función sea definida antes de su primer uso, debe conocer el orden en que se ejecutan las instrucciones, lo que se denomina flujo de ejecución.
La ejecución siempre comienza con la primera sentencia del programa. Las sentencias se ejecutan una a la vez, en orden descendente.
Las definiciones de función no alteran el flujo de ejecución del programa, pero se debe recordar que las sentencias dentro de la función no se ejecutan hasta que se llama a la función.
Una llamada a función es como un desvío en el flujo de ejecución. En lugar de pasar a la siguiente sentencia, el flujo salta al cuerpo de la función, ejecuta las sentencias que están allí y luego regresa para continuar el código donde lo dejó.
Esto suena bastante simple, hasta que se tiene en cuenta que una función puede llamar a otra. Mientras se está ejecutando una función, el programa podría tener que ejecutar las sentencias de otra función. Luego, mientras ejecuta esa nueva función, ¡el programa podría tener que ejecutar otra función más!
Afortunadamente, Julia es capaz de hacer el seguimiento de sus movimientos, así que cada vez que una función termina, el programa retoma la función que la llamó justo donde la dejó. Cuando llega al final del programa, la ejecución termina.
En resumen, cuando lee un programa, no siempre debe leer de arriba hacia abajo. A veces tiene más sentido seguir el flujo de ejecución.
Parámetros y argumentos
Algunas de las funciones que se han visto requieren argumentos. Por ejemplo, la función cos necesita un número como argumento. Algunas funciones toman más de un argumento; por ejemplo parse toma dos: un número y una cadena.
Dentro de la función, los argumentos se asignan a variables llamadas parámetros. A continuación se muestra un ejemplo de definición de función que toma un argumento:
function imprimirdosveces(juan)
println(juan)
println(juan)
endEsta función asigna el argumento a un parámetro llamado juan. Cuando se llama a la función, esta imprime el valor del parámetro (cualquiera que sea) dos veces.
Esta función funciona con cualquier valor que se pueda imprimir.
julia> imprimirdosveces("Correo no deseado")
Correo no deseado
Correo no deseado
julia> imprimirdosveces(42)
42
42
julia> imprimirdosveces(π)
π = 3.1415926535897 ...
π = 3.1415926535897 ...Las mismas reglas de composición que se aplican a las funciones integradas también se aplican a las funciones definidas por el programador, por lo que podemos usar cualquier tipo de expresión como argumento para imprimirdosveces:
julia> imprimirdosveces("Correo no deseado "^4)
Correo no deseado Correo no deseado Correo no deseado Correo no deseado
Correo no deseado Correo no deseado Correo no deseado Correo no deseado
julia> imprimirdosveces(cos(π))
-1.0
-1.0El argumento se evalúa antes de llamar a la función, por lo que en los ejemplos las expresiones "Correo no deseado "^4 y cos(π) solo se evalúan una vez.
También puede usar una variable como argumento:
julia> michael = "La vida es bella."
"La vida es bella."
julia> imprimirdosveces(michael)
La vida es bella.
La vida es bella.El nombre de la variable que pasamos como argumento (michael) no tiene nada que ver con el nombre del parámetro (juan). Para la función imprimirdosveces todos los parámetros se llaman juan, sin importar el nombre de la variable que pasemos como argumento (en este caso michael).
Las variables y los parámetros son locales
Cuando se crea una variable dentro de una función, esta es local, es decir, solo existe dentro de la función. Por ejemplo:
function concatenar_dos(parte1, parte2)
concat = parte1 * parte2
imprimirdosveces(concat)
endEsta función toma dos argumentos, los concatena e imprime el resultado dos veces. Aquí hay un ejemplo:
julia> linea1 = "Hola hola"
"Hola hola"
julia> linea2 = "adiós adiós."
"adiós adiós".
julia> concatenar_dos(línea1, línea2)
Hola hola adiós adiós.
Hola hola adiós adiós.Cuando concatenar_dos termina, la variable concat es destruida. Si intentamos imprimirla, obtendremos un error:
julia> println(concat)
ERROR: UndefVarError: concat not definedLos parámetros también son locales. Por ejemplo, fuera de la función imprimirdosveces, no existe juan.
Diagramas de pila
Para seguir la pista de qué variables se usan en qué lugares es útil dibujar un diagrama de pila. Al igual que los diagramas de estado, los diagramas de pila muestran el valor de cada variable, pero también muestran la función a la que pertenece cada una.
Cada función se representa por un marco. Un marco es un recuadro con el nombre de una función a un costado, y los parámetros y variables de la función dentro. El diagrama de pila para el ejemplo anterior se muestra en Figura 2.
Los marcos se ordenan de tal manera que cada función llama a la función inmediatamente inferior. En este ejemplo, imprimirdosveces fue llamado por concatenar_dos, y concatenar_dos fue llamado por Main, que es un nombre especial para la función de más alto nivel. Cuando se crea una variable afuera de cualquier función, pertenece a Main.
Cada parámetro se refiere al mismo valor que su argumento correspondiente. Entonces, parte1 tiene el mismo valor que linea1, parte2 tiene el mismo valor que linea2, y juan tiene el mismo valor que concat.
Si se produce un error durante una llamada a función, Julia imprime el nombre de la función, el nombre de la función que la llamó, el nombre de la función que a su vez llamó a esta otra, y así sucesivamente hasta llegar a la función de más alto nivel Main.
Por ejemplo, si intenta acceder a concat desde imprimirdosveces, obtendrá un UndefVarError:
ERROR: UndefVarError: concat not defined Stacktrace: [1] imprimirdosveces at ./REPL[1]>:2 [inlined] [2] concatenar_dos(::String, ::String) at ./REPL[2]>:3
Esta lista de funciones se llama trazado inverso. Indica en qué archivo de programa se produjo el error, en qué línea y qué funciones se estaban ejecutando en ese momento. También muestra la línea de código que causó el error.
El orden de las funciones en el trazado inverso es el opuesto del orden de los recuadros en el diagrama de pila. La función que se está ejecutando actualmente está en la parte superior.
Funciones productivas y funciones nulas
Algunas de las funciones que hemos utilizado, como las funciones matemáticas, devuelven resultados. A este tipo de funciones se les llamará funciones productivas, a falta de un nombre mejor. Otras funciones como imprimirdosveces, realizan una acción pero no devuelven un valor. Estas se llaman funciones nulas.
Cuando se llama a una función productiva, casi siempre se quiere hacer algo con el resultado; por ejemplo, asignarlo a una variable o usarlo como parte de una expresión:
x = cos(radianes)
aurea = (sqrt(5)+1)/2Cuando se llama a una función en modo interactivo, Julia muestra el resultado:
julia> sqrt(5)
2.23606797749979Pero en un script, si se llama a una función productiva, ¡el valor de retorno se pierde para siempre!
sqrt(5)Output:
2.23606797749979
Este script calcula la raíz cuadrada de 5, pero como no almacena ni muestra el resultado, no es muy útil.
Las funciones nulas pueden mostrar algo en la pantalla o tener algún otro efecto, pero no tienen un valor de retorno. Si asigna el resultado a una variable, obtendrá un valor especial llamado nothing (nada en inglés).
julia> resultado = imprimirdosveces("Bing")
Bing
Bing
julia> show(resultado)
nothingPara imprimir el valor nothing, debe usar la función show que es como la función print pero permite el valor nothing.
El valor nothing no es lo mismo que la cadena "nothing". Es un valor especial que tiene su propio tipo:
julia> typeof (nothing)
NothingLas funciones que hemos escrito hasta ahora son nulas. Comenzaremos a escribir funciones productivas en unos pocos capítulos.
¿Por qué se necesitan funciones?
Puede que no esté claro por qué vale la pena dividir un programa en funciones. Hay varias razones:
-
Crear una nueva función le brinda la oportunidad de darle nombre a un grupo de sentencias, lo que hace que su programa sea más fácil de leer y depurar.
-
Las funciones pueden hacer que un programa sea más corto al eliminar código repetitivo. Además, si realiza un cambio, solo tiene que hacerlo en un solo lugar.
-
Dividir un programa largo en funciones le permite depurar las partes de una en una y luego unirlas.
-
Las funciones bien diseñadas pueden ser útiles para muchos programas. Una vez que escribe y depura una, puede reutilizarla.
-
En Julia, las funciones pueden mejorar mucho el rendimiento.
Depuración
Una de las habilidades más importantes que adquirirá es la depuración. Aunque puede ser frustrante, la depuración es una de las partes más intelectualmente gratificantes, desafiantes e interesantes de la programación.
La depuración puede ser vista como un trabajo de detective. El programador se enfrenta a pistas y tiene que inferir los procesos y eventos que generaron los resultados que ve.
La depuración también es como una ciencia experimental. Una vez que se tiene una idea de lo que está mal, se modifica el programa y se intenta nuevamente. Si la hipótesis era correcta, se puede predecir el resultado de la modificación y así estar un paso más cerca de un programa totalmente funcional. Si la hipótesis era incorrecta, se tiene que encontrar una nueva. Como Sherlock Holmes señaló:
Cuando todo aquello que es imposible ha sido eliminado, lo que quede, por muy improbable que parezca, es la verdad.
El signo de los cuatro
Para algunas personas, la programación y la depuración son lo mismo. Es decir, la programación es el proceso de depurar gradualmente un programa hasta que haga lo que desea. Lo ideal es comenzar con un programa que funcione y hacer pequeñas modificaciones, depurándolas a medida que avanza.
Por ejemplo, Linux es un sistema operativo que contiene millones de líneas de código, pero comenzó como un programa simple que Linus Torvalds usó para explorar el chip Intel 80386. Según Larry Greenfield, "Uno de los proyectos anteriores de Linus fue un programa que cambiaría entre imprimir" AAAA "y" BBBB ". Esto luego evolucionó a Linux ". (The Linux Users'’ Guide Beta Version 1).
Glosario
- función
-
secuencia de sentencias que ejecuta una operación deseada y tiene un nombre. Las funciones pueden tomar o no argumentos, y pueden producir o no un resultado.
- definición de función
-
Una sentencia que crea una nueva función, especificando su nombre, parámetros y las sentencias que contiene.
- objeto de función
-
Un valor creado por una definición de función. El nombre de la función es una variable que se refiere a un objeto de función.
- encabezado
-
La primera línea de una definición de función.
- cuerpo
-
Secuencia de sentencias dentro de una definición de función.
- parámetro
-
Un nombre usado dentro de una función para referirse al valor pasado como argumento.
- Llamada a función
-
Una sentencia que ejecuta una función. Compuesta por el nombre de la función seguido por la lista de argumentos que usa entre paréntesis.
- argumento
-
Valor que se le pasa a una función cuando se la llama. Este valor se asigna al parámetro correspondiente en la función.
- variable local
-
Una variable definida dentro de una función. Una variable local solo puede usarse dentro de su función.
- valor de retorno
-
El resultado de una función. Si se utiliza una llamada a función como una expresión, el valor de retorno es el valor de la expresión.
- función productiva
-
Una función que devuelve un valor.
- función vacía
-
Una función que siempre devuelve
nothing. nothing-
Un valor especial devuelto por las funciones nulas.
- composición
-
Usar una expresión como parte de una expresión más grande, o una sentencia como parte de una sentencia más grande.
- flujo de ejecución
-
El orden en que las sentencias se ejecutan.
- diagrama de pila
-
Una representación gráfica de una pila de funciones, sus variables y los valores a los que se refieren.
- marco
-
Un recuadro que en un diagrama de pila representa una llamada de función. Contiene las variables locales y los parámetros de la función.
- trazado inverso
-
Una lista de las funciones que se están ejecutando, las cuales son impresas cuando ocurre una excepción.
Ejercicios
|
Observación
|
Estos ejercicios deben realizarse utilizando sólo lo que se ha tratado hasta ahora. |
Ejercicio 3-2
Escriba una función llamada justificar_a_la_derecha que tome una cadena s como parámetro y que imprima la cadena con suficientes espacios en blanco para que la última letra de la cadena se encuentre en la columna 70 de la pantalla.
using IntroAJuliajustificar_a_la_derecha("Celia")|
Observación
|
Use concatenación de cadenas y repetición. Además, Julia tiene integrada una función llamada |
Ejercicio 3-3
Un objeto de función es un valor que se puede asignar a una variable o ser pasado como argumento. Por ejemplo, dosveces es una función que toma un objeto de función como argumento y lo llama dos veces:
function dosveces(f)
f()
f()
endA continuación se muestra un ejemplo que usa dosveces para llamar a una función llamada imprimirgato dos veces.
function imprimirpalabra()
println("palabra")
end
dosveces(imprimirpalabra)-
Escriba este ejemplo en un script y pruébelo.
-
Modifique
dosvecespara que tome dos argumentos: un objeto de función y un valor, y que llame a la función dos veces, pasando el valor como argumento. -
Copie la definición de
imprimirdosvecesmencionada antes en este capítulo a su secuencia de comandos. -
Use la versión modificada de
dosvecespara llamar aimprimirdosvecesdos veces, pasando"palabra"como argumento. -
Defina una nueva función llamada
cuatrovecesque tome un objeto de función y un valor, y que llame a la función cuatro veces, pasando el valor como parámetro. Debe haber solo dos sentencias en el cuerpo de esta función, no cuatro.
Ejercicio 3-4
-
Escriba la función
imprimircuadriculaque dibuje una cuadrícula como la siguiente:
julia> imprimircuadricula()
+ - - - - + - - - - +
| | |
| | |
| | |
| | |
+ - - - - + - - - - +
| | |
| | |
| | |
| | |
+ - - - - + - - - - +-
Escriba una función que dibuje una cuadrícula similar con cuatro filas y cuatro columnas.
Créditos: Este ejercicio se basa en un ejercicio en Oualline, Practical C Programming, Third Edition, O’Reilly Media, 1997.
|
Observación
|
Para imprimir más de un valor por línea, se puede imprimir una secuencia de valores separados por comas: La función El resultado de estas sentencias es |
4. Estudio de Caso: Diseño de Interfaz
Este capítulo presenta un segundo estudio de caso, que muestra el proceso de diseñar funciones que trabajen en conjunto.
Se presentan gráficos turtle, que es una forma de crear dibujos a través de la programación. Los gráficos turtle no están incluidos en la Biblioteca Estándar, por lo que se debe agregar el módulo IntroAJulia a su configuración de Julia.
Los ejemplos de este capítulo se pueden ejecutar en un notebook gráfico en JuliaBox, el cual combina código, texto formateado, matemáticas y multimedia en un solo documento (vea Apéndice B).
Turtles
Un modulo es un archivo que contiene una colección de funciones relacionadas. Julia proporciona algunos módulos en su Biblioteca Estándar. Además, es posible agregar más funciones a una gran cantidad de paquetes (https://juliaobserver.com).
Los paquetes se pueden instalar en REPL ingresando al modo Pkg REPL con la tecla ].
(v1.2) pkg> add https://github.com/JuliaIntro/IntroAJulia.jlEsto puede demorar un poco.
Antes de que podamos usar las funciones de un módulo, tenemos que importarlo con una sentencia using:
julia> using IntroAJulia
julia> 🐢 = Turtle()
Luxor.Turtle(0.0, 0.0, true, 0.0, (0.0, 0.0, 0.0))El módulo IntroAJulia proporciona una función llamada Turtle (tortuga en español) que crea un objeto Luxor.Turtle, el cual es asignado a una variable llamada 🐢 (\:turtle: TAB).
Una vez que crea una tortuga, puede llamar a una función para "moverla", y así hacer un dibujo con ella. Por ejemplo, para mover la tortuga hacia adelante (forward en inglés):
@svg begin
forward(🐢, 100)
endLa palabra reservada @svg ejecuta una macro que dibuja una imagen SVG. Las macros son una característica importante pero avanzada de Julia.
Los argumentos de forward son la tortuga y una distancia en píxeles, por lo que el tamaño real depende de su pantalla.
También es posible hacer girar a la tortuga con la función turn. Los argumentos de esta función son la tortuga y un ángulo en grados.
Además, cada tortuga está sosteniendo un lápiz, que puede estar hacia arriba o hacia abajo; si el lápiz está hacia abajo, la tortuga deja un rastro cuando se mueve. Figura 3 muestra el rastro dejado por la tortuga. Las funciones penup y pendown significan "lápiz hacia arriba" y "lápiz hacia abajo".
Para dibujar un ángulo recto, modifique la llamada a la macro:
🐢 = Turtle()
@svg begin
forward(🐢, 100)
turn(🐢, -90)
forward(🐢, 100)
endEjercicio 4-1
Ahora modifique la macro para que dibuje un cuadrado. ¡No sigas hasta haberlo terminado!
Repetición Simple
Es probable que haya escrito algo como esto:
🐢 = Turtle()
@svg begin
forward(🐢, 100)
turn(🐢, -90)
forward(🐢, 100)
turn(🐢, -90)
forward(🐢, 100)
turn(🐢, -90)
forward(🐢, 100)
endSe puede hacer lo mismo de manera más concisa con una sentencia for:
julia> for i in 1:4
println("¡Hola!")
end
¡Hola!
¡Hola!
¡Hola!
¡Hola!Este es el uso más simple de la sentencia for, aunque se verán más usos después. Ésto debería ser suficiente para reescribir su programa que dibuja un cuadrado. No continúe hasta que lo haga.
Aquí hay una sentencia for que dibuja un cuadrado:
🐢 = Turtle()
@svg begin
for i in 1:4
forward(🐢, 100)
turn(🐢, -90)
end
endLa sintaxis de una sentencia for es similar a la definición de una función. Tiene un encabezado y un cuerpo que termina con la palabra reservada end. El cuerpo puede contener el número de sentencias que desee.
Una sentencia for también es llamada bucle porque el flujo de ejecución recorre el cuerpo y luego vuelve a la parte superior. En este caso, ejecuta el cuerpo cuatro veces.
Esta versión es en realidad un poco diferente del código anterior que dibujaba un cuadrado porque hace otro giro después de dibujar el último lado del cuadrado. El giro adicional lleva más tiempo, pero simplifica el código si se hace lo mismo en cada iteración del ciclo. Esta versión también tiene el efecto de dejar a la tortuga nuevamente en la posición inicial, mirando hacia la dirección inicial.
Ejercicios
Los siguientes ejercicios usan tortugas. Son divertidos, pero también tienen un trasfondo. Mientras trabaja en ellos, piense cuál es ese trasfondo.
|
Observación
|
Las siguientes secciones muestran las soluciones para estos ejercicios, así que no mire hasta que haya terminado (o al menos lo haya intentado). |
Ejercicio 4-2
Escriba una función llamada cuadrado que tome como parámetro a un turtle t. Debería usar este turtle para dibujar un cuadrado.
Ejercicio 4-3
Escriba una llamada a función que pase t como argumento a cuadrado, y luego vuelva a ejecutar la macro.
Ejercicio 4-4
Agregue otro parámetro, llamado lon, a cuadrado. Modifique el cuerpo para que la longitud de los lados sea lon, y luego modifique la llamada a función agregando este segundo argumento. Ejecute la macro nuevamente. Pruebe con un rango de valores para lon.
Ejercicio 4-5
Haga una copia de cuadrado y cambie su nombre a polígono. Agregue otro parámetro llamado n y modifique el cuerpo para que dibuje un polígono regular de \(n\)-lados.
|
Observación
|
Los ángulos exteriores de un polígono regular de \(n\)-lados son \(\frac{360}{n}\) grados. |
Ejercicio 4-6
Escriba una función llamada círculo que tome un turtle t y un radio r como parámetros, y que dibuje un círculo aproximado llamando a polígono con una longitud y número de lados apropiados. Pruebe su función con un rango de valores de r.
|
Observación
|
Calcule la circunferencia del círculo y asegúrese de que |
Ejercicio 4-7
Haga una versión más general de circulo llamada arco que tome un parámetro adicional angulo y que determine qué fracción de un círculo dibujar. angulo está en grados, entonces cuando angulo= 360, arco debería dibujar un círculo completo.
Encapsulación
El primer ejercicio le pide que coloque el código que permite dibujar un cuadrado en una definición de función, y que luego llame a la función, pasando a turtle como parámetro. Aquí hay una solución:
function cuadrado(t)
for i in 1:4
forward(t, 100)
turn(t, -90)
end
end
🐢 = Turtle()
@svg begin
cuadrado(🐢)
endLas sentencias más internas, forward y turn tienen doble sangría para mostrar que están dentro del bucle for, que a su vez está dentro de la definición de función.
Dentro de la función, t se refiere a la misma tortuga 🐢, entonces turn(t, -90) tiene el mismo efecto que turn(🐢, -90). En ese caso, ¿por qué no llamar al parámetro 🐢? La razón es que t puede ser cualquier tortuga, no solo 🐢, por lo que podríamos crear una segunda tortuga y pasarla como argumento a cuadrado:
🐫 = Turtle()
@svg begin
cuadrado(🐫)
endColocar una porción de código en una función se denomina encapsulación. Uno de los beneficios de la encapsulación es que al ponerle un nombre al código, esto sirve como una especie de documentación. Otra ventaja es que si reutiliza el código, ¡es más conciso llamar a una función dos veces que copiar y pegar el cuerpo!
Generalización
El siguiente paso es agregar un parámetro lon a cuadrado. Aquí hay una solución:
function cuadrado(t, lon)
for i in 1:4
forward(t, lon)
turn(t, -90)
end
end
🐢 = Turtle()
@svg begin
cuadrado(🐢, 100)
endAgregar un parámetro a una función se llama generalización porque hace que la función sea más general: en la versión anterior, el cuadrado siempre tenía el mismo tamaño; en esta versión puede ser de cualquier tamaño.
El siguiente paso también es una generalización. En vez de dibujar cuadrados, poligono dibuja polígonos regulares con cualquier número de lados. Aquí hay una solución:
function poligono(t, n, lon)
angulo = 360 / n
for i in 1:n
forward(t, lon)
turn(t, -angulo)
end
end
🐢 = Turtle()
@svg begin
poligono(🐢, 7, 70)
endEste ejemplo dibuja un polígono de 7 lados, con una longitud de 70 por lado.
Diseño de Interfaz
El siguiente paso es escribir circulo, que toma un radio r como parámetro. Aquí hay una solución simple que usa poligono para dibujar un polígono de 50 lados:
function circulo(t, r)
circunferencia = 2 * π * r
n = 50
lon = circunferencia / n
poligono(t, n, lon)
endLa primera línea calcula la circunferencia de un círculo con radio \(r\) usando la fórmula \(2 \pi r\). n es el número de segmentos de línea de nuestra aproximación a un círculo, y lon es la longitud de cada segmento. Por lo tanto, polígono dibuja un polígono de 50 lados que se aproxima a un círculo de radio r.
Una limitante de esta solución es que n es constante, lo que significa que para círculos muy grandes, los segmentos de línea son demasiado largos, y para círculos pequeños, perdemos tiempo dibujando segmentos muy pequeños. Una solución sería generalizar la función tomando n como parámetro. Esto le daría al usuario (quien llama a círculo) más control pero la interfaz sería menos pulcra.
La interfaz de una función es un resumen de cómo se usa: ¿cuáles son los parámetros? ¿Qué hace la función? ¿Y cuál es el valor de retorno? Una interfaz es "pulcra" si le permite al usuario que la llama hacer lo que quiera sin tener que lidiar con detalles innecesarios.
En este ejemplo, r pertenece a la interfaz porque especifica el círculo a dibujar. n es menos apropiado porque se refiere a los detalles de cómo se debe representar el círculo.
En lugar de saturar la interfaz, es mejor elegir un valor apropiado de n dependiendo de la circunferencia:
function circulo(t, r)
circunferencia = 2 * π * r
n = trunc(circunferencia / 3) + 3
lon = circunferencia / n
poligono(t, n, lon)
endAhora, el número de segmentos es un número entero cercano a circunferencia/3, por lo que la longitud de cada segmento es aproximadamente 3, que es lo suficientemente pequeño como para que los círculos se vean bien, pero lo suficientemente grandes como para ser eficientes y aceptables para cualquier círculo.
Agregar 3 a n garantiza que el polígono tenga al menos 3 lados.
Refactorización
Cuando se escribió circulo, se pudo reutilizar poligono ya que un polígono de muchos lados es una buena aproximación de un círculo. Pero arco no es tan versátil; no se puede usar poligono o circulo para dibujar un arco.
Una alternativa es comenzar con una copia de poligono y transformarla en arco. El resultado podría verse así:
function arco(t, r, angulo)
arco_lon = 2 * π * r * angulo / 360
n = trunc(arco_lon / 3) + 1
paso_lon = arco_lon / n
paso_angulo = angulo / n
for i in 1:n
forward(t, paso_lon)
turn(t, -paso_angulo)
end
endLa segunda mitad de esta función se parece a poligono, pero no se puede reutilizar poligono sin cambiar la interfaz. Se podría generalizar poligono para tomar un angulo como tercer argumento, ¡pero entonces poligono ya no sería un nombre apropiado! En su lugar, se puede llamar a esta función más general polilinea:
function polilinea(t, n, lon, angulo)
for i in 1:n
forward(t, lon)
turn(t, -angulo)
end
endAhora se puede reescribir poligono y arco usando polilinea:
function poligono(t, n, lon)
angulo = 360 / n
polilinea(t, n, lon, angulo)
end
function arco(t, r, angulo)
arco_lon = 2 * π * r * angulo / 360
n = trunc(arco_lon / 3) + 1
paso_lon = arco_lon / n
paso_angulo = angulo / n
polilinea(t, n, paso_lon, paso_angulo)
endFinalmente, se puede reescribir circulo usando arco:
function circulo(t, r)
arco(t, r, 360)
endEste proceso, que reorganiza un programa para mejorar las interfaces y facilitar la reutilización del código, se denomina refactorización. En este caso, se observa que había un código similar en arco y poligono, por lo que lo "factorizamos" en polilinea.
Si se hubiese planeado con anticipación, se podría haber escrito polilinea primero y haber evitado la refactorización, pero a menudo no se sabe lo suficiente al comienzo de un proyecto para diseñar todas las interfaces. Una vez que se comienza a programar, se comprende mejor el problema. A veces, refactorizar es una señal de que se ha aprendido algo.
Un Plan de Desarrollo
Un plan de desarrollo de programa es un proceso para escribir programas. El proceso que se utiliza en este estudio de caso es "encapsulación y generalización". Los pasos de este proceso son:
-
Comience escribiendo un pequeño programa sin definiciones de funciones.
-
Una vez que el programa funcione, identifique una porción de código que tenga un objetivo específico, encapsule esta porción en una función y asígnele un nombre.
-
Generalice la función agregando los parámetros apropiados.
-
Repita los pasos 1–3 hasta que tenga un conjunto de funciones. De ser posible, copie y pegue código para evitar volver a escribir (y volver a depurar).
-
Busque oportunidades para mejorar el programa refactorizando. Por ejemplo, si tiene un código similar en varios lugares, considere factorizarlo en una función general apropiada.
Este proceso tiene algunos inconvenientes, se explorarán alternativas más adelante, pero puede ser útil si no sabe de antemano cómo dividir el programa en funciones. Este enfoque permite diseñar conforme se avanza.
Docstring
Un docstring es una cadena que va antes de una función y que explica la interfaz ("doc" es la abreviatura de "documentación"). Aquí hay un ejemplo:
"""
polilinea(t, n, lon, angulo)
Dibuja n segmentos de línea de la longitud dada y con
ángulo entre ellos (en grados) dado. t es una tortuga.
"""
function polilinea(t, n, lon, angulo)
for i in 1:n
forward(t, lon)
turn(t, -angulo)
end
endSe puede acceder a la documentación en REPL o en un notebook escribiendo ? seguido del nombre de una función o macro, y presionando ENTER:
help?> polilinea search: polilinea(t, n, lon, angulo) Dibuja n segmentos de línea de la longitud dada y con ángulo entre ellos (en grados) dado. t es una tortuga.
Los docstring generalmente son cadenas de comillas triples, también conocidas como cadenas de líneas múltiples ya que las comillas triples permiten que la cadena abarque más de una línea.
Un docstring contiene la información esencial que alguien necesitaría para usar esta función. Explica de manera concisa lo que hace la función (sin entrar en detalles sobre cómo lo hace). Explica qué efecto tiene cada parámetro en el comportamiento de la función y de qué tipo debe ser cada parámetro (si no es obvio).
|
Observación
|
Escribir este tipo de documentación es una parte importante del diseño de la interfaz. Una interfaz bien diseñada debe ser simple de explicar; si tiene dificultades para explicar una de sus funciones, tal vez la interfaz podría mejorarse. |
Depuración
Una interfaz es como un contrato entre una función y el usuario. El usuario acepta proporcionar ciertos parámetros y la función acepta hacer cierto trabajo.
Por ejemplo, polilinea requiere cuatro argumentos: t tiene que ser una tortuga; n tiene que ser un número entero; lon debería ser un número positivo; y angulo tiene que ser un número, en grados.
Estos requisitos se llaman precondiciones porque se supone que son verdaderos antes de que la función comience a ejecutarse. Por el contrario, las condiciones al final de la función son postcondiciones. Las postcondiciones incluyen el efecto deseado de la función (como dibujar segmentos de línea) y cualquier efecto secundario (como mover la tortuga o hacer otros cambios).
Las condiciones previas son responsabilidad del usuario. Si el usuario viola una precondición (¡debidamente documentada!) y la función no funciona correctamente, el error está en el usuario, no en la función.
Si se cumplen las precondiciones pero no las postcondiciones, el error está en la función. Si sus pre y postcondiciones son claras, pueden ayudar con la depuración.
Glosario
- modulo
-
Un archivo que contiene una colección de funciones relacionadas y otras definiciones.
- paquete
-
Una biblioteca externa con más funcionalidades.
- sentencia using
-
Una sentencia que lee un archivo de módulo y crea un objeto de módulo.
- bucle
-
Una parte de un programa que puede ejecutarse repetidamente.
- encapsulación
-
El proceso de transformar una secuencia de sentencias en una definición de función.
- generalización
-
El proceso de reemplazar algo innecesariamente específico (como un número) con algo más general (como una variable o parámetro).
- interfaz
-
Una descripción de cómo usar una función, incluido el nombre y las descripciones de los argumentos y el valor de retorno.
- refactorización
-
El proceso de modificar un programa para mejorar las interfaces de las funciones y otras cualidades del código.
- plan de desarrollo de programa
-
Un proceso para escribir programas.
- docstring
-
Una cadena que aparece en la parte superior de una definición de función para documentar la interfaz de la función.
- precondición
-
Un requisito que debe cumplir el usuario antes de que comience una función.
- postcondición
-
Un requisito que debe cumplir la función antes de que finalice.
Ejercicios
Ejercicio 4-8
Copie y pegue el código de este capítulo en un notebook.
-
Dibuje un diagrama de pila que muestre el estado del programa mientras ejecuta
circulo(🐢, radio). Puede hacer la aritmética a mano o agregar sentencias de impresión al código. -
La versión de
arcoen Sección 4.7 no es muy precisa ya que la aproximación lineal del círculo siempre queda por afuera del círculo verdadero. Como resultado, la tortuga termina a unos pocos píxeles del destino correcto. La siguiente solución muestra una forma de reducir el efecto de este error. Lea el código y vea si tiene sentido. Si dibuja un diagrama, es posible que entienda mejor cómo funciona.
"""
arco(t, r, angulo)
Dibuja un arco con el radio y el ángulo dados:
t: tortuga
r: radio
angulo: ángulo subtendido por el arco, en grados
"""
function arco(t, r, angulo)
arco_lon = 2 * π * r * abs(angulo) / 360
n = trunc(arco_lon / 4) + 3
paso_lon = arco_lon / n
paso_angulo = angulo / n
# haciendo un ligero giro a la izquierda antes de comenzar se reduce
# el error causado por la aproximación lineal del arco
turn(t, -paso_angulo/2)
polilinea(t, n, paso_lon, paso_angulo)
turn(t, paso_angulo/2)
endEjercicio 4-9
Escriba un conjunto de funciones generales que permitan dibujar flores como en Figura 4.
Ejercicio 4-10
Escriba un conjunto de funciones generales que puedan dibujar formas como en Figura 5.
Ejercicio 4-11
Las letras del alfabeto se pueden construir a partir de un número pequeño de elementos básicos, como líneas verticales y horizontales, y algunas curvas. Diseñe un alfabeto que se pueda dibujar con un número mínimo de elementos básicos y luego escriba funciones que dibujen las letras.
Debería escribir una función para cada letra, con nombres dibujar_a, dibujar_b, etc., y colocar sus funciones en un archivo llamado letras.jl.
Ejercicio 4-12
Lea sobre espirales en https://es.wikipedia.org/wiki/Espiral; luego escriba un programa que dibuje una espiral de Arquímedes como en Figura 6.
5. Condicionales y recursividad
El tema principal de este capítulo es la sentencia if, la cual permite ejecutar diferentes acciones dependiendo del estado del programa. Inicialmente se presentan dos nuevos operadores: división entera y módulo.
División entera y Módulo
El operador división entera, ÷ (\div TAB), divide dos números y redondea hacia abajo el resultado. Por ejemplo, suponga que la duración de una película es de 105 minutos. Es posible que desee saber la duración en horas. La división convencional devuelve un número de punto flotante:
julia> minutos = 105
105
julia> minutos / 60
1.75No obstante, las horas no se suelen escribir con decimales. La división entera devuelve el número entero de horas, redondeado hacia abajo:
julia> horas = minutos ÷ 60
1Para obtener el resto de la división, se puede restar una hora (en minutos) a la duración total de la película:
julia> resto = minutos - horas * 60
45Otra alternativa es usar el operador módulo, %, que divide dos números y devuelve el resto.
julia> resto = minutos % 60
45|
Observación
|
El operador módulo es más útil de lo que parece. Permite verificar, por ejemplo, si un número es divisible por otro: si Además, puede extraer el (o los) dígito(s) más a la derecha de un número. Por ejemplo, |
Expresiones booleanas
Una expresión booleana es una expresión que es verdadera o falsa. Los siguientes ejemplos usan el operador ==, que compara dos operandos, y devuelve el valor true (verdadero en español) si son iguales, y el valor false (falso) de lo contrario.
julia> 5 == 5
true
julia> 5 == 6
falsetrue y false son valores especiales que pertenecen al tipo Bool, no son cadenas:
julia> typeof(true)
Bool
julia> typeof(false)
BoolEl operador == es un operador relacional. El resto de operadores relacionales son:
x != y # x no es igual a y
x ≠ y # (\ne TAB)
x > y # x es mayor que y
x < y # x es menor que y
x >= y # x es mayor o igual que y
x ≥ y # (\ge TAB)
x <= y # x es menor o igual que y
x ≤ y # (\le TAB)|
Aviso
|
Aunque estas operaciones probablemente le sean familiares, los símbolos de Julia son diferentes de los símbolos matemáticos. Un error común es usar un solo signo igual ( |
Operadores Lógicos
Hay tres operadores lógicos: && (y), || (o) y ! (no). La semántica (significado) de estos operadores es similar a su significado en español. Por ejemplo, x>0 && x<10 es verdadero solo si x es mayor que 0 y menor que 10.
n%2==0 || n%3 == 0 es verdadero si una o ambas condiciones son verdaderas, es decir, si el número es divisible por 2 o por 3.
Tanto && como || se asocian en primer lugar con el objeto a su derecha, pero && tiene preferencia por sobre ||.
Finalmente, el operador ! niega una expresión booleana, entonces !(x>y) es verdadero si x>y es falso, es decir, si x es menor o igual que y.
Ejecución Condicional
Para escribir programas útiles, generalmente se necesita verificar condiciones y cambiar el comportamiento del programa acorde a ellas. Las sentencias condicionales permiten llevar esto a cabo. La forma más simple es la sentencia if ("si" en inglés):
if x > 0
println("x es positivo")
endLa expresión booleana después de if se llama condición. Si es verdadera, se ejecuta la instrucción con sangría. Si no, nada ocurre.
Las sentencias if tienen la misma estructura que las definiciones de función: un encabezado seguido del cuerpo, terminado con la palabra reservada end (en español "fin"). Las sentencias como esta se denominan sentencias compuestas.
No hay límite en el número de sentencias que pueden aparecer en el cuerpo. A veces es útil tener un cuerpo sin sentencias (por lo general, como un marcador de posición para el código que aún no se ha escrito).
if x < 0
# TODO: se necesita realizar alguna acción con los valores negativos!
endEjecución alternativa
Una segunda forma de la sentencia if es la "ejecución alternativa", en la que hay dos posibilidades y la condición determina cuál se ejecuta. La sintaxis se ve así:
if x % 2 == 0
println("x es par")
else
println("x es impar")
endSi el resto de x dividido por 2 es 0, entonces x es par y el programa muestra un mensaje acorde. Si la condición es falsa, se ejecuta el segundo conjunto de sentencias. Como la condición debe ser verdadera o falsa, se ejecutará exactamente una de las alternativas. Las alternativas se llaman ramas, porque son ramas en el flujo de ejecución.
Condicionales encadenadas
A veces hay más de dos posibilidades y se necesitan más de dos ramas. Una manera de expresar este cómputo es a través de una condicional encadenada:
if x < y
println("x es menor que y")
elseif x > y
println("x es mayor que y")
else
println("x e y son iguales")
endDe nuevo, sólo se ejecutará una rama. No hay límite al número de sentencias elseif. Si hay una sentencia else, debe estar al final (aunque no es necesario que esté).
if alternativa == "a"
dibujar_a()
elseif alternativa == "b"
dibujar_b()
elseif alternativa == "c"
dibujar_c()
endCada condición se comprueba en orden. Si la primera es falsa, se comprueba la siguiente, y así se sigue con las demás. Si una de ellas es verdadera, se ejecuta la rama correspondiente y la sentencia se termina. Si es verdadera más de una condición, sólo se ejecuta la primera rama verdadera.
Condicionales anidadas
Una condicional puede estar anidada ("nested" en inglés) dentro de otra. Podríamos haber escrito el ejemplo de la sección anterior de la siguiente manera:
if x == y
println("x e y son iguales")
else
if x < y
println("x es menor a y")
else
println("x es mayor a y")
end
endLa condicional externa contiene dos ramas. La primera rama contiene una sentencia simple. La segunda rama contiene otra sentencia if, que tiene dos ramas propias. Estas dos ramas son ambas sentencias simples, aunque podrían ser sentencias condicionales.
Aunque la sangría no obligatoria de las sentencias hace evidente su estructura, las condicionales anidadas muy pronto se vuelven difíciles de leer. Se recomienda evitarlas cuando pueda.
Los operadores lógicos a menudo proporcionan una forma de simplificar las sentencias condicionales anidadas. Por ejemplo, es posible reescribir el siguiente código usando un solo condicional:
if 0 < x
if x < 10
println("x es un número positivo de un solo dígito.")
end
endLa sentencia print sólo se ejecuta si conseguimos superar ambas condicionales, de modo que se puede obtener el mismo efecto con el operador &&:
if 0 < x && x < 10
println("x es un número positivo de un solo dígito.")
endPara este tipo de condición, Julia proporciona una sintaxis más concisa:
if 0 < x < 10
println("x es un número positivo de un solo dígito.")
endRecursividad
Está permitido que una función llame a otra y también que una función se llame a sí misma. Puede no parecer útil, pero sí lo es, como puede verse en la siguiente función:
function cuentaregresiva(n)
if n ≤ 0
println("Despegue!")
else
print(n, " ")
cuentaregresiva(n-1)
end
endSi n es 0 o negativo, muestra la palabra "Despegue!". En otro caso, muestra el valor n y luego llama a la función cuentaregresiva, pasándole n-1 como argumento.
¿Qué sucede si llamamos a una función como esta?
julia> cuentaregresiva(3)
3 2 1 Despegue!La ejecución de cuentaregresiva empieza con n = 3, y como n es mayor que 0, muestra el valor 3, y luego se llama a sí misma…
La ejecución de cuentaregresiva empieza con n = 2, y como n es mayor que 0,
muestra el valor 2, y luego se llama a sí misma…
La ejecución de cuentaregresiva empieza con n = 1, y como n es mayor que 0,
muestra el valor 1, y luego se llama a sí misma…
La ejecución de cuentaregresiva empieza con n = 0, y como n no es mayor que 0,
muestra la palabra "Despegue!" y luego termina.
La cuentaregresiva cuyo argumento es n = 1 termina.
La cuentaregresiva cuyo argumento es n = 2 termina.
La cuentaregresiva cuyo argumento es n = 3 termina.
Y volvemos a Main.
Una función que se llama a sí misma es una función recursiva y el proceso de ejecución se llama recursividad.
Como otro ejemplo, se puede escribir una función que imprima una cadena \(n\) veces.
function printn(s, n)
if n ≤ 0
return
end
println(s)
printn(s, n-1)
endSi n <= 0, se usa la sentencia return para salir de la función. El flujo de la ejecución vuelve inmediatamente a la sentencia de llamada a función y no se ejecutan las líneas restantes de la función.
El resto de la función es similar a cuenta regresiva: muestra s y luego se llama a sí misma para mostrar s \(n-1\) veces más de modo que el número de lineas mostradas es \(1 + (n - 1)\), es decir \(n\).
Para ejemplos simples como este, es más fácil usar un ciclo for. Se mostrarán ejemplos que son difíciles de escribir con un ciclo for y fáciles de escribir con recursividad.
Diagramas de pila para funciones recursivas
En Sección 3.9 se usó un diagrama de pila para representar el estado de un programa durante una llamada de función. El mismo tipo de diagrama puede ser de utilidad para interpretar una función recursiva.
Cada vez que se llama a una función, Julia crea un marco que contiene las variables locales de la función y los parámetros. En una función recursiva, puede haber más de un marco en el diagrama de pila al mismo tiempo.
Figura 7 muestra un diagrama de pila para cuentaregresiva utilizando n=3.
Como siempre, la parte superior de la pila es el marco para Main. Está vacío pues no se crearon variables en Main ni tampoco se pasaron argumentos.
Los cuatro marcos de cuentaregresiva tienen diferentes valores del parámetro n. La parte inferior del diagrama de pila, donde n = 0, es llamado caso base. No hace una llamada recursiva, así que no hay más marcos.
Ejercicio 5-1
Como ejercicio, dibuje un diagrama de pila para printn, llamada con s = "Hola" y n = 2. Luego escriba una función llamada hacer_n, que tome como argumentos una función y un número n, y que luego llame a la función dada \(n\) veces.
Recursión infinita
Si una recursión nunca alcanza un caso base, continúa haciendo llamadas recursivas para siempre y el programa nunca termina. Esto se conoce como recursión infinita y generalmente no es una buena idea. Aquí hay un código con una recursión infinita:
function recursion()
recursion()
endEn la mayoría de los entornos de programación, un programa con recursión infinita realmente no se ejecuta para siempre. Julia entrega un mensaje de error cuando se alcanza la profundidad de recursión máxima:
julia> recursion()
ERROR: StackOverflowError:
Stacktrace:
[1] recursion() at ./REPL[1]:2 (repeats 80000 times)Este stacktrace es un poco más grande que el que vimos en el capítulo anterior. Cuando se produce el error, ¡hay 80000 marcos de recursion en el diagrama de pila!
Si por accidente encuentra una recursión infinita en su código, revise su función para confirmar que hay un caso base que no realiza una llamada recursiva. Si hay un caso base, verifique si realmente puede ocurrir.
Entrada por teclado
Los programas que se han escrito hasta ahora no aceptan entradas del usuario. Simplemente hacen lo mismo cada vez.
Julia tiene una función incorporada llamada readline que detiene el programa y espera a que el usuario escriba algo. Cuando el usuario presiona RETURN o ENTER, el programa se reanuda y readline devuelve lo que el usuario escribió como una cadena.
julia> text = readline()
¿Qué está esperando?
"¿Qué está esperando?"Antes de recibir una entrada por teclado del usuario, es una buena idea imprimir un mensaje que le diga al usuario qué escribir:
julia> print("¿Cuál... es su nombre? "); readline()
¿Cuál... es su nombre? ¡Arturo, Rey de los Bretones!
"¡Arturo, Rey de los Bretones!"Un punto y coma ; permite colocar varias sentencias en la misma línea. En el REPL solo la última sentencia devuelve su valor.
Si espera que el usuario escriba un número entero, puede intentar convertir el valor de retorno a Int64:
julia> println("¿Cuántos dejaron su casa, su tierra o su posesión?"); numero = readline()
¿Cuántos dejaron su casa, su tierra o su posesión?
115
"115"
julia> parse(Int64, numero)
115Pero si el usuario no escribe una cadena de dígitos, obtendrá un error:
julia> println("¿Cuántos dejaron su casa, su tierra o su posesión?"); numero = readline()
¿Cuántos dejaron su casa, su tierra o su posesión?
Más de ciento quince son.
"Más de ciento quince son."
julia> parse(Int64, speed)
ERROR: ArgumentError: invalid base 10 digit 'M' in "Más de ciento quince son."
[...]Veremos qué hacer con este tipo de error más adelante.
Depuración
Cuando se produce un error de sintaxis o de tiempo de ejecución, el mensaje de error contiene mucha información, lo cual puede ser abrumador. Las partes más útiles suelen ser:
-
Qué tipo de error fue
-
Dónde ocurrió tal error
Los errores de sintaxis suelen ser fáciles de encontrar y hay algunos trucos. En general, los mensajes de error indican dónde se descubrió el problema pero el error real podría estar antes en el código, a veces en una línea anterior.
Lo mismo aplica para los errores de tiempo de ejecución. Suponga que está tratando de calcular una relación señal/ruido en decibelios. La fórmula es
En Julia, se podría escribir algo como esto:
intensidad_señal = 9
intensidad_ruido = 10
relacion = intensidad_señal ÷ intensidad_ruido
decibeles = 10 * log10(relacion)
print(decibeles)Obteniendo:
-InfEste no es el resultado que esperábamos.
Para encontrar el error, puede ser útil imprimir el valor de la variable "relacion", que resulta ser 0. El problema está en la línea 3, que usa la división entera en lugar de la división de punto flotante.
|
Aviso
|
El usuario debe tomarse el tiempo de leer los mensajes de error cuidadosamente, pero no se debe asumir que todo lo que dicen es correcto. |
Glosario
- División entera
-
Un operador, denotado por
÷, que divide dos números y redondea hacia abajo (hacia el infinito negativo) a un entero. - operador módulo
-
Un operador, denotado con el signo de porcentaje (%), que se utiliza con enteros y devuelve el resto cuando un número se divide por otro.
- expresión booleana
-
Una expresión cuyo valor es
verdaderoofalso. - operador relacional
-
Uno de los operadores que compara sus operandos:
==,≠(!=),>,<,≥(>=), and≤(<=). - operador lógico
-
Uno de los operadores que combina expresiones booleanas:
&&(and),||(or), and!(not). - sentencia condicional
-
Una sentencia que controla el flujo de ejecución dependiendo de alguna condición.
- condición
-
La expresión booleana en una sentencia condicional que determina qué rama se ejecuta.
- sentencia compuesta
-
Una sentencia que consta de un encabezado y un cuerpo. El cuerpo termina con la palabra reservada
end. - rama
-
Una de las secuencias alternativas de sentencias en una sentencia condicional.
- condicional encadenada
-
Una sentencia condicional con una serie de ramas alternativas.
- condicional anidada
-
Una sentencia condicional que aparece en una de las ramas de otra sentencia condicional.
- sentencia return
-
Una sentencia que hace que una función finalice de inmediato y que vuelva a la sentencia de llamada a función.
- recursividad o recursión
-
El proceso de llamar a la función que se está ejecutando actualmente.
- caso base
-
Una rama condicional en una función recursiva que no realiza una llamada recursiva.
- recursión infinita
-
Una recursión que no tiene un caso base o que nunca llega a él. Eventualmente, una recursión infinita provoca un error de tiempo de ejecución.
Ejercicios
Ejercicio 5-2
La función time devuelve el tiempo medio de Greenwich actual en segundos desde "la época", que es un tiempo arbitrario utilizado como punto de referencia. En sistemas UNIX, la época es el 1 de enero de 1970.
julia> time()
1.603600382165353e9Escriba un script que lea la hora actual y la convierta a una hora del día en horas, minutos y segundos, más el número de días transcurridos desde la época.
Ejercicio 5-3
El último teorema de Fermat dice que no hay enteros positivos \(a\), \(b\), and \(c\) tal que
para cualquier valor de \(\ (n \) mayor que 2.
-
Escriba una función llamada
verificarfermatque tome cuatro parámetros—a,b,cyn— y que verifique si el teorema de Fermat es válido. Sines mayor que 2 ya^n + b^n == c^nel programa debería imprimir, "¡Santo cielo, Fermat estaba equivocado!" De lo contrario, el programa debería imprimir, "No, eso no funciona". -
Escriba una función que solicite al usuario ingresar valores para
a,b,cyn, que los convierta en enteros y que useverificarfermatpara verificar si violan el teorema de Fermat.
Ejercicio 5-4
Si tiene tres barras, estas podrían o no formar un triángulo. Por ejemplo, si una de las barras tiene 12 centímetros de largo y las otras dos tienen un centímetro de largo, no es posible que las barras pequeñas puedan juntarse al medio. Para cualquier trío de longitudes, hay una prueba simple para ver si es posible formar un triángulo:
|
Observación
|
Si cualquiera de las tres longitudes es mayor que la suma de las otras dos, entonces no se puede formar un triángulo. De lo contrario, se puede. (Si la suma de dos longitudes es igual a la tercera, forman lo que se llama un triángulo "degenerado"). |
-
Escriba una función llamada
estrianguloque tome tres enteros como argumentos, y que imprima “Sí” o “No”, dependiendo de si se puede o no formar un triángulo a partir de barras de las longitudes dadas. -
Escriba una función que solicite al usuario ingresar tres longitudes de barras, las convierta en enteros y use
estriangulopara verificar si las barras con las longitudes dadas pueden formar un triángulo.
Ejercicio 5-5
¿Cuál es el resultado del siguiente programa? Dibuje un diagrama de pila que muestre el estado del programa cuando imprima el resultado.
function recursion(n, s)
if n == 0
println(s)
else
recursion(n-1, n+s)
end
end
recursion(3, 0)-
¿Qué pasaría si se llamara a esta función así:
recursion(-1, 0)? -
Escriba un documento que explique todo lo que alguien necesitaría saber para usar esta función (y nada más).
Los siguientes ejercicios utilizan el módulo IntroAJulia, descrito en Capítulo 4:
Ejercicio 5-6
Lea la siguiente función y vea si puede averiguar qué hace (vea los ejemplos en Capítulo 4). Luego ejecútelo y vea si lo hizo bien.
function dibujar(t, distancia, n)
if n == 0
return
end
angulo = 50
adelante(t, distancia*n)
girar(t, -angulo)
dibujar(t, distancia, n-1)
girar(t, 2*angulo)
dibujar(t, distancia, n-1)
girar(t, -angulo)
adelante(t, -distancia*n)
endEjercicio 5-7
La curva de Koch es un fractal que luce como Figura 8. Para dibujar una curva de Koch con longitud \(x\), todo lo que tiene que hacer es
-
Dibuje una curva de Koch con longitud \(\frac{x}{3}\).
-
Gire a la izquierda 60 grados.
-
Dibuje una curva de Koch con longitud \(\frac{x}{3}\).
-
Gire a la derecha 120 grados.
-
Dibuje una curva de Koch con longitud \(\frac{x}{3}\).
-
Gire a la izquierda 60 grados.
-
Dibuje una curva de Koch con longitud \(\frac{x}{3}\).
La excepción es cuando \(x\) es menor que 3: en ese caso, puede dibujar una línea recta con una longitud \(x\).
-
Escribe una función llamada
kochque tome una tortuga y una longitud como parámetros y que use la tortuga para dibujar una curva de Koch con la longitud dada. -
Escriba una función llamada
copodenieveque dibuje tres curvas de Koch para hacer el contorno de un copo de nieve. -
La curva de Koch se puede generalizar de varias maneras. Consulte https://en.wikipedia.org/wiki/Koch_snowflake para ver ejemplos e implementar su favorito.
6. Funciones productivas
Muchas de las funciones de Julia que se han utilizado, como las funciones matemáticas, producen valores de retorno. Todas las funciones que se han escrito hasta ahora son nulas, es decir, tienen un efecto (como imprimir un valor) pero devuelven el valor nothing. En este capítulo se enseña a escribir funciones productivas.
Valores de retorno
Llamar a una función genera un valor de retorno, que generalmente se asigna a una variable o se usa como parte de una expresión.
e = exp(1.0)
altura = radio * sin(radio)Las funciones que se han escrito hasta ahora son nulas. Coloquialmente hablando, no tienen valor de retorno; de manera formal, su valor de retorno es nothing. En este capítulo, (finalmente) se van a escribir funciones productivas. El primer ejemplo es area, que devuelve el área de un círculo dado un radio:
function area(radio)
a = π * radio^2
return a
endSe ha visto la sentencia return antes pero en una función productiva la sentencia return incluye una expresión. Esta sentencia significa: "Retorne inmediatamente de esta función y use la siguiente expresión como valor de retorno". La expresión dada puede ser arbitrariamente complicada. Así pues, se podría haber escrito esta función más concisamente:
function area(radio)
π * radio^2
endEl valor devuelto por una función es el valor de la última expresión evaluada, que, por defecto, es la última expresión en el cuerpo de la definición de la función.
Por otro lado, las variables temporales como a, y las sentencias return explícitas pueden facilitar la depuración.
A veces es útil tener múltiples sentencias return, una en cada rama de una sentencia condicional:
function valorabsoluto(x)
if x < 0
return -x
else
return x
end
endDado que estas sentencias return están en una condicional alternativa, solo se ejecuta una.
En cuanto se ejecuta una sentencia return, la función termina sin ejecutar ninguna de las sentencias siguientes. El código que aparece después de la sentencia return, o en cualquier otro lugar al que el flujo de ejecución nunca llegará, se llama código muerto.
En una función productiva, es una buena idea asegurarse que cualquier posible recorrido del programa llegue a una sentencia return. Por ejemplo:
function valorabsoluto(x)
if x < 0
return -x
end
if x > 0
return x
end
endEsta versión no es correcta porque si x es igual a 0, ninguna de las condiciones es verdadera y la función termina sin alcanzar una sentencia return. Si el flujo de ejecución llega al final de la función, el valor de retorno es nothing, que claramente no es el valor absoluto de 0.
julia> show(valorabsoluto(0))
nothing|
Observación
|
Julia tiene una función incorporada llamada |
Ejercicio 6-1
Escriba la función comparar que tome dos valores, x y y, y que devuelva 1 si x > y, 0 si x == y, y -1 si x < y.
Desarrollo incremental
Conforme vaya escribiendo funciones más extensas puede empezar a dedicar más tiempo a la depuración.
Para lidiar con programas de complejidad creciente, se sugiere una técnica llamada desarrollo incremental. El objetivo del desarrollo incremental es evitar largas sesiones de depuración, añadiendo y probando solamente pequeñas porciones de código cada vez.
Por ejemplo, suponga que desea encontrar la distancia entre dos puntos dados por las coordenadas \(\left(x_1, y_1\right)\) y \(\left(x_2, y_2\right)\). Por el teorema de Pitágoras, la distancia es:
El primer paso es considerar qué aspecto tendría la función distancia en Julia. En otras palabras, ¿cuáles son las entradas (parámetros) y cuál es la salida (valor de retorno)?
En este caso las entradas son los dos puntos, que se pueden representar usando cuatro números. El valor devuelto es la distancia, que es un número de punto flotante.
He aquí una primera versión de la función:
function distancia(x₁, y₁, x₂, y₂)
0.0
endObviamente esta versión de la función no calcula distancias sino que siempre devuelve cero. Aun así, es correcta sintácticamente hablando y se ejecutará, lo que implica que se puede probar antes de hacerla más compleja. Los números de subíndice están disponibles en la codificación de caracteres Unicode (\_1 TAB, \_2 TAB, etc.).
Para probar la nueva función, se llama con una muestra de valores:
distance(1, 2, 4, 6)Se eligen estos valores de tal forma que la distancia horizontal sea igual a 3 y la distancia vertical sea igual a 4 y de esa manera el resultado es 5 (la hipotenusa del triángulo 3-4-5). Cuando se comprueba una función, es útil conocer la respuesta correcta.
Hasta el momento se ha podido confirmar que la función es sintácticamente correcta, por lo que se puede empezar a agregar líneas de código. El paso lógico siguiente es encontrar las diferencias \(x_2 - x_1\) y \(y_2 - y_1\). En la siguiente versión de la función se almacenarán estos valores en variables temporales y se mostrarán con el macro @show.
function distancia(x₁, y₁, x₂, y₂)
dx = x₂ - x₁
dy = y₂ - y₁
@show dx dy
0.0
endSi la función trabaja bien, las salidas deben ser dx = 3 y dy = 4. Si es así, se sabe que la función está obteniendo los parámetros correctos y realizando el primer cálculo correctamente. Si no, entonces sólo hay unas pocas líneas que revisar.
A continuación se calcula la suma de los cuadrados de dx y dy:
function distancia(x₁, y₁, x₂, y₂)
dx = x₂ - x₁
dy = y₂ - y₁
d² = dx^2 + dy^2
@show d²
0.0
endDe nuevo se quiere ejecutar el programa en esta etapa y comprobar la salida (que debería ser 25). Los números en superíndice también están disponibles (\^2 TAB). Finalmente, se puede usar sqrt para calcular y devolver el resultado:
function distancia(x₁, y₁, x₂, y₂)
dx = x₂ - x₁
dy = y₂ - y₁
d² = dx^2 + dy^2
sqrt(d²)
endSi esto funciona correctamente, ya se habría terminado. Si no, se podría mostrar el valor de la variable resultado antes de la sentencia de retorno.
La versión final de la función no muestra nada cuando se ejecuta, sólo retorna un valor. Las sentencias print son útiles para la depuración, pero una vez que el programa esté funcionando correctamente, se deben eliminar. El código eliminado se llama andamiaje porque es útil para construir el programa pero no es parte del producto final.
Al principio, debería añadir solamente una o dos líneas de código cada vez. Conforme vaya ganando experiencia, puede que se encuentre escribiendo y depurando fragmentos mayores de código. Sin embargo, el proceso de desarrollo incremental puede ahorrarle mucho tiempo de depuración.
Los aspectos clave del proceso son:
-
Iniciar con un programa que funcione y hacerle pequeños cambios incrementales. En cualquier momento, si hay un error, sabrá exactamente dónde está.
-
Usar variables temporales para guardar valores intermedios para que pueda mostrarlos y verificarlos.
-
Una vez que el programa esté funcionando, tal vez prefiera eliminar parte del andamiaje o consolidar múltiples sentencias en expresiones compuestas, pero sólo si eso no hace que el programa sea difícil de leer.
Ejercicio 6-2
Use la técnica de desarrollo incremental para escribir una función llamada hipotenusa que retorne el largo de la hipotenusa de un triángulo rectángulo dado el largo de las otras dos aristas. Registre cada etapa del proceso de desarrollo.
Composición
Ahora, como usted esperaría, se puede llamar a una función desde otra. Como ejemplo, se escribe una función que tome dos puntos, el centro del círculo y un punto del perímetro, y calcule el área del círculo.
Suponga que el punto central está almacenado en las variables xc y yc, y que el punto del perímetro lo está en xp y yp. El primer paso es hallar el radio del círculo, que es la distancia entre los dos puntos. La función distancia que realiza esta tarea sería:
radio = distancia(xc, yc, xp, yp)El siguiente paso es encontrar el área del círculo usando este radio. De nuevo se usa una de las funciones definidas previamente:
resultado = area(radio)Envolviendo todo en una función, se obtiene:
function areacirculo(xc, yc, xp, yp)
radio = distancia(xc, yc, xp, yp)
resultado = area(radio)
return resultado
endLas variables temporales radio y resultado son útiles para el desarrollo y la depuración, pero una vez que el programa está funcionando, se puede hacer más conciso componiendo las llamadas a función:
function areacirculo(xc, yc, xp, yp)
area(distancia(xc, yc, xp, yp))
endFunciones Booleanas
Las funciones pueden devolver valores booleanos, lo que a menudo es conveniente para ocultar complicadas comprobaciones dentro de funciones. Por ejemplo:
function esdivisible(x, y)
if x % y == 0
return true
else
return false
end
endEs común dar a las funciones booleanas nombres que suenan como preguntas que tienen como respuesta un si ó un no, esdivisible devuelve true o false para indicar si x es o no divisible por y.
Por ejemplo:
julia> esdivisible(6, 4)
false
julia> esdivisible(6, 3)
trueEl resultado del operador == es booleano, por lo tanto se puede escribir la función de una manera más concisa devolviendo el resultado directamente:
function esdivisible(x, y)
x % y == 0
endLas funciones booleanas se usan a menudo en las sentencias condicionales:
if esdivisible(x, y)
println("x es divisible por y")
endPuede parecer tentador escribir algo como:
if esdivisible(x, y) == true
println("x es divisible por y")
endpero la comparación extra con true es innecesaria.
Ejercicio 6-3
Escriba la función entremedio(x,y,z) que devuelva true si x ≤ y ≤ z, o false en otro caso.
Más recursividad
Solo se ha cubierto una pequeña parte de Julia pero le puede interesar saber que esta parte ya es un lenguaje de programación completo, lo que significa que cualquier cómputo puede expresarse en este lenguaje. Cualquier programa que se haya escrito podría reescribirse usando solo lo que ha aprendido hasta ahora (en realidad, necesitaría algunos comandos para controlar dispositivos como el mouse, discos, etc., pero eso es todo).
Probar esta afirmación es un ejercicio no trivial realizado por primera vez por Alan Turing, uno de los primeros científicos de la computación (algunos argumentarían que era matemático, pero muchos de los primeros científicos informáticos comenzaron como matemáticos). En consecuencia, esto se conoce como la Tesis de Turing. Para una discusión más completa (y precisa) de la Tesis de Turing, se recomienda el libro de Michael Sipser Introducción a la Teoría de la Computación.
Para darle una idea de lo que puede hacer con las herramientas que ha aprendido hasta ahora, se evalúan algunas funciones matemáticas definidas recursivamente. Una definición recursiva es similar a una definición circular, en el sentido de que la definición contiene una referencia a lo que está siendo definido. Una definición verdaderamente circular no es muy útil:
- vorpal
-
Un adjetivo usado para describir algo que es vorpal.
Si esta definición apareciese en el diccionario, la persona que la leyera podría molestarse. Por otro lado, si se busca la definición de la función factorial, denotada con el símbolo \(!\), se encuentra encontrar algo como esto:
Esta definición dice que el factorial de 0 es 1, y el factorial de cualquier otro valor \(n\), es \(n\) multiplicado por el factorial de \(n-1\).
Entonces \(3!\) es 3 veces \(2!\), que es 2 veces \(1!\), que es 1 vez \(0!\). Es decir, \(3!\) es igual a 3 por 2 por 1 por 1, que es 6.
Si se puede escribir una definición recursiva, se puede escribir un programa de Julia para evaluarlo. El primer paso es decidir cuáles deberían ser los parámetros. En este caso, debe quedar claro que factorial toma valores enteros:
function fact(n) endSi el argumento es 0, la función debe devolver 1:
function fact(n)
if n == 0
return 1
end
endDe lo contrario, y esto es lo interesante, se tiene que hacer una llamada recursiva para encontrar el factorial de n-1 y luego multiplicarlo por n:
function fact(n)
if n == 0
return 1
else
recursion = fact(n-1)
resultado = n * recursion
return resultado
end
endEl flujo de ejecución de este programa es similar al flujo de cuentaregresiva en Sección 5.8. Si llamamos a fact con el valor 3:
Como 3 no es 0, se toma la segunda rama y se calcula el factorial de n-1 …
Como 2 no es 0, se toma la segunda rama y se calcula el factorial de n-1 …
Como 1 no es 0, se toma la segunda rama y se calcula el factorial de + n-1 + …
Como 0 es igual a 0, se toma la primera rama y devuelve 1 sin realizar
más llamadas recursivas.
El valor de retorno, 1, se multiplica por n, que es 1, y se devuelve el resultado.
El valor de retorno, 1, se multiplica por n, que es 2, y se devuelve el resultado.
El valor de retorno 2 se multiplica por n, que es 3, y el resultado, 6, se convierte en el valor de retorno de la llamada a función que inició todo el proceso.
Figura 9 muestra cómo se ve el diagrama de pila para esta secuencia de llamadas a funciones.
Los valores de retorno se pasan de nuevo a la pila. En cada marco, el valor de retorno es el valor de resultado, que es el producto de n y recursion.
En el último marco, las variables locales recursion y resultado no existen, porque la rama que las crea no se ejecuta.
|
Observación
|
Julia tiene la función |
Voto de confianza
Seguir el flujo de ejecución es una forma de leer programas, pero puede llegar a ser abrumador. Una alternativa es lo que se conoce como el "voto de confianza"(en inglés, "leap of faith"). Cuando llega a una llamada de función, en lugar de seguir el flujo de ejecución, asume que la función funciona correctamente y devuelve el resultado correcto.
De hecho, ya se está dando este voto de confianza cuando se usan funciones integradas de Julia. Cuando se llaman a cos o exp, no se examinan los cuerpos de esas funciones. Simplemente se asume que funcionan porque las personas que las escribieron eran buenos programadores.
Lo mismo ocurre cuando el usuario llama a una de sus propias funciones. Por ejemplo, en Sección 6.4, se escribe una función llamada esdivisible que determina si un número es divisible por otro. Una vez que se confirme que esta función es correcta —al examinar y probar el código—, se puede usar la función sin mirar nuevamente el cuerpo.
Lo mismo aplica a los programas recursivos. Cuando llegue a la llamada recursiva, en lugar de seguir el flujo de ejecución, debe suponer que la llamada recursiva funciona (devuelve el resultado correcto) y luego preguntarse: "Suponiendo que pueda encontrar el factorial de \(n-1\), ¿se puede calcular el factorial de \(n\)?" Está claro que es posible, multiplicando por \(n\).
Por supuesto, es un poco extraño suponer que la función funciona correctamente cuando no ha terminado de escribirla, ¡pero por eso se llama voto de confianza!
Un Ejemplo Más
Después de los factoriales, el ejemplo más común de una función matemática definida de manera recursiva es fibonacci, que tiene la siguiente definición (ver https://en.wikipedia.org/wiki/Fibonacci_number):
Traducido a Julia, se ve así:
function fib(n)
if n == 0
return 0
elseif n == 1
return 1
else
return fib(n-1) + fib(n-2)
end
endSi intenta seguir el flujo de ejecución en esta función, incluso para valores bastante pequeños de n, su cabeza podría estallar. Dando un voto de confianza, es decir, asumiendo que las dos llamadas recursivas funcionan correctamente, entonces está claro que se obtiene el resultado correcto al sumarlas.
Tipos de Comprobación
¿Qué pasa si se llama a fact con 1.5 como argumento?
julia> fact(1.5)
ERROR: StackOverflowError:
Stacktrace:
[1] fact(::Float64) at ./REPL[3]:2Parece una recursión infinita. ¿Como es esto posible? La función tiene un caso base (cuando n == 0). Pero si n no es un número entero, es posible perderse el caso base y hacer recursión para siempre.
En la primera llamada recursiva, el valor de n es 0.5. En la siguiente, es -0.5. A partir de ahí, se vuelve más pequeño (más negativo), pero nunca será 0.
Existen dos opciones. Se puede intentar generalizar la función factorial para trabajar con números de punto flotante, o se puede hacer que fact verifique el tipo del argumento. La primera opción se llama función gamma y está un poco más allá del alcance de este libro. En este libro se proseguirá con la segunda.
Se puede usar el operador integrado isa para verificar el tipo de argumento. También podemos asegurarnos de que el argumento sea positivo:
function fact(n)
if !(n isa Int64)
error("El factorial únicamente está definido para números enteros.")
elseif n < 0
error("El factorial no está definido para enteros negativos.")
elseif n == 0
return 1
else
return n * fact(n-1)
end
endEl primer caso base se hace cargo de números no enteros y el segundo de enteros negativos. En ambos casos, el programa imprime un mensaje de error y devuelve nothing para indicar que algo salió mal:
julia> fact("fred")
ERROR: El factorial únicamente está definido para números enteros.
julia> fact(-2)
ERROR: El factorial no está definido para enteros negativos.Si se superan ambas verificaciones, se sabe que n es positivo o cero, por lo que es posible probar que la recursión termina.
Este programa muestra un patrón a veces llamado guardian. Los dos primeros condicionales actúan como guardianes, protegiendo el código que sigue de los valores que pueden causar un error. Los guardianes hacen posible demostrar que el código es correcto.
En Sección 14.5 se explorará una alternativa más flexible para imprimir un mensaje de error: generar una excepción.
Depuración
Dividir un código extenso en pequeñas funciones crea naturalmente puntos de control para la depuración. Si un programa no está funcionando, existen tres posibilidades a considerar:
-
Hay algo incorrecto en los argumentos de la función, se viola una condición previa.
-
Hay algo incorrecto en la función, se viola una condición posterior.
-
Hay algo incorrecto en el valor de retorno o la forma en que se está utilizando.
Para descartar la primera posibilidad, puede agregar una sentencia de impresión al comienzo de la función para mostrar los valores de los parámetros (y tal vez sus tipos) o bien escribir líneas de código que verifiquen las condiciones previas de manera explícita.
Si los parámetros están bien, agregue una sentencia de impresión antes de cada sentencia return y muestre el valor de retorno. Si es posible, verifique el resultado a mano. Considere también llamar a la función con valores que faciliten la verificación del resultado (como en Sección 6.2).
Si la función parece estar funcionando, revise la llamada a la función para asegurarse de que el valor de retorno se está utilizando correctamente (¡o incluso si se está utilizando!).
Agregar sentencias de impresión al principio y al final de una función puede ayudar a que el flujo de ejecución sea más transparente. Por ejemplo, aquí hay una versión de fact con sentencias de impresión:
function fact(n)
espacio = " " ^ (4 * n)
println(espacio, "factorial ", n)
if n == 0
println(espacio, "devolviendo 1")
return 1
else
recursion = fact(n-1)
resultado = n * recursion
println(espacio, "devolviendo ", resultado)
return resultado
end
endespacio es una cadena de caracteres de espacios que permite generar sangría en la salida:
julia> fact(4)
factorial 4
factorial 3
factorial 2
factorial 1
factorial 0
devolviendo 1
devolviendo 1
devolviendo 2
devolviendo 6
devolviendo 24
24Si está confundido con el flujo de ejecución, este tipo de salida puede ser útil. Desarrollar un buen andamiaje toma tiempo, pero un poco de andamiaje puede ahorrar al usuario mucha depuración.
Glosario
- variable temporal
-
Variable usada para almacenar un valor intermedio en un cálculo complejo.
- código muerto
-
Parte de un programa que nunca puede ser ejecutado, a menudo porque aparece después de una sentencia
return. - desarrollo incremental
-
Plan de desarrollo de un programa que intenta evitar la depuración agregando y probando solamente una pequeña porción de código a la vez.
- andamiaje
-
Código que se usa durante el desarrollo de un programa pero que no es parte de la versión final del mismo.
- guardián
-
Un patrón de programación que usa una sentencia condicional para verificar y manejar circunstancias que pueden causar un error.
Ejercicios
Ejercicio 6-4
Dibuje un diagrama de pila para el siguiente programa. ¿Qué imprime el programa?
function b(z)
prod = a(z, z)
println(z, " ", prod)
prod
end
function a(x, y)
x = x + 1
x * y
end
function c(x, y, z)
total = x + y + z
cuadrado = b(total)^2
cuadrado
end
x = 1
y = x + 1
println(c(x, y+3, x+y))Ejercicio 6-5
La función de Ackermann, \(A(m, n)\), se define:
Vea https://en.wikipedia.org/wiki/Ackermann_function. Escriba una función llamada ack que evalúe la función de Ackermann. Use su función para evaluar ack(3, 4), que debería ser 125. ¿Qué sucede para valores mayores de m y n?
Ejercicio 6-6
Un palíndromo es una palabra que se escribe igual en un sentido que en otro, como "ana" y "radar". De manera recursiva, una palabra es un palíndromo si la primera y la última letra son iguales y lo que está entre ellas es un palíndromo.
Las siguientes funciones toman un argumento de tipo cadena y devuelven la primera letra, la última, y las intermedias:
function primera(palabra)
primera = firstindex(palabra)
palabra[primera]
end
function ultima(palabra)
ultima = lastindex(palabra)
palabra[ultima]
end
function medio(palabra)
primera = firstindex(palabra)
ultima = lastindex(palabra)
palabra[nextind(palabra, primera) : prevind(palabra, ultima)]
endSe verá cómo funcionan en Capítulo 8.
-
Pruebe estas funciones. ¿Qué sucede si llama a la función
mediocon una cadena de dos letras? ¿Y con una cadena de una letra? ¿Qué pasa con la cadena vacía"", que no contiene letras? -
Escriba una función llamada
espalindromoque tome un argumento de tipo cadena y devuelvatruesi es un palíndromo yfalsede lo contrario. Recuerde que puede usar la función integradalengthpara verificar la longitud de una cadena.
Ejercicio 6-7
Un número, \(a\), es una potencia de \(b\) si es divisible por \(b\) y \(\frac{a}{b}\) es una potencia de \(b\). Escriba una función llamada espotencia que tome los parámetros a y b y devuelva true si a es una potencia de b.
|
Observación
|
Tendrá que pensar en el caso base. |
Ejercicio 6-8
El máximo común divisor (MCD) de \(a\) y \(b\) es el número más grande que los divide a ambos con resto 0.
Una forma de encontrar el MCD de dos números se basa en la observación de que si \(r\) es el resto cuando \(a\) se divide por \(b\), entonces mcd(a, b) = mcd(b, r). Como caso base, podemos usar mcd(a, 0) = a.
Escriba una función llamada mcd que tome los parámetros a y b y devuelva su máximo divisor común.
Créditos: Este ejercicio se basa en un ejemplo del libro Estructura e interpretación de programas informáticos de Abelson y Sussman.
7. Iteración
Este capítulo se centra en la iteración, que es la capacidad de ejecutar repetidamente un bloque de sentencias. Se han visto dos tipos de iteración: usando recursión en Sección 5.8 y usando ciclos for, en Sección 4.2. En este capítulo veremos otro tipo más: usando sentencias while. Primeramente, se introducirán algunos términos sobre asignación de variables.
Asignación múltiple
Puede que ya haya descubierto que está permitido realizar más de una asignación a la misma variable. Una nueva asignación hace que la variable existente se refiera a un nuevo valor (y deje de referirse al viejo valor).
julia> x = 5
5
julia> x = 7
7La primera vez que se muestra x su valor es 5, y la segunda vez su valor es 7
Figura 10 muestra el aspecto de una asignación múltiple en un diagrama de estado.
Es necesario aclarar algo que puede causar confusión. Puesto que Julia usa el signo igual (=) para la asignación, es tentador interpretar una sentencia a = b como una sentencia de igualdad. Pero esta interpretación es incorrecta.
Para empezar, la igualdad es simétrica y la asignación no lo es. Por ejemplo, en matemáticas, si \(a=7\) entonces \(7=a\). Pero en Julia la sentencia a = 7 es válida, y 7 = a no lo es.
Además, en matemáticas, una sentencia de igualdad es verdadera o falsa siempre. Si \(a=b\) ahora, entonces \(a\) siempre será igual a \(b\). En Julia, una sentencia de asignación puede hacer que dos variables sean iguales, pero no tienen por qué quedarse así:
julia> a = 5
5
julia> b = a # a y b son iguales
5
julia> a = 3 # a y b ya no son iguales
3
julia> b
5La tercera línea cambia el valor de a pero no cambia el valor de b, por lo tanto ya dejan de ser iguales.
|
Aviso
|
Reasignar variables puede ser útil, pero se debe tener precaución. Si los valores cambian frecuentemente, la reasignación puede hacer que el código sea difícil de leer y depurar. Está permitido definir una función con el mismo nombre de una variable definida anteriormente. |
Actualización de variables
Una de las formas más comunes de asignación múltiple es la actualización, dónde el nuevo valor de la variable depende del anterior.
julia> x = x + 1
8Esto significa “tome el valor actual de x, súmele uno, y después actualice x con el nuevo valor.”
Si intenta actualizar una variable que no existe obtendrá un error, puesto que Julia evalúa la expresión del lado derecho antes de asignar un valor a x:
julia> y = y + 1
ERROR: UndefVarError: y not definedAntes de actualizar una variable tiene que inicializarla, usualmente con una asignación simple:
julia> y = 0
0
julia> y = y + 1
1Actualizar una variable sumándole 1 se denomina un incremento y restándole 1 se llama un decremento.
La Sentencia while
Las computadoras se usan a menudo para automatizar tareas repetitivas. Realizar repetidamente tareas idénticas o similares sin cometer errores es algo que las computadoras hacen bien y que los seres humanos hacen limitadamente. La ejecución repetida de un conjunto de sentencias se llama iteración.
Ya se han visto dos funciones, cuentaregresiva y printn, que iteran usando recursividad. Por ser la iteración tan común, Julia proporciona varias características que la hacen más fácil. Una es la sentencia for que se vio en Sección 4.2, a la cual se volverá más adelante.
Otra característica es la sentencia while. Aquí hay una versión de cuentaregresiva que muestra el uso de la sentencia while:
function cuentaregresiva(n)
while n > 0
print(n, " ")
n = n - 1
end
println("¡Despegue!")
endCasi podría leer la sentencia while como si fuera Español. La función anterior significa: “Mientras n sea mayor que 0, continúe mostrando el valor de n y luego reduciendo el valor de n en 1. Cuando llegue a 0, muestre la palabra ¡Despegue!“
Más formalmente, el flujo de ejecución de una sentencia while es el siguiente:
-
Se determina si la condición es verdadera o falsa.
-
Si es falsa, se sale de la sentencia while y continúa la ejecución con la siguiente sentencia.
-
Si es verdadera, ejecuta cada una de las sentencias en el cuerpo y regresa al paso 1.
Este tipo de flujo se llama bucle porque el tercer paso vuelve a la parte superior.
El cuerpo del bucle debería cambiar el valor de una o más variables de manera que, en algún momento, la condición sea falsa y el bucle termine. En caso contrario, el bucle se repetirá indefinidamente, lo cual se llama bucle infinito. Una interminable fuente de diversión para los informáticos es la observación de que las instrucciones del champú “Enjabone, enjuague, repita”, son un bucle infinito.
En el caso de cuentaregresiva, podemos probar que el bucle termina: si n es cero o negativo, el ciclo termina. En otro caso, el valor de n se hace más pequeño cada vez que pasa por el bucle, así en cierto momento se llega a 0.
En otros casos no es tan fácil decirlo. Por ejemplo:
function seq(n)
while n != 1
println(n)
if n % 2 == 0 # n is par
n = n / 2
else # n is impar
n = n*3 + 1
end
end
endLa condición de este bucle es n != 1, de manera que el bucle continuará hasta que n sea 1, que hará que la condición sea falsa.
Cada vez que pasa por el bucle, el programa muestra como salida el valor de n y luego comprueba si es par o impar. Si es par, el valor de n se divide por dos. Si es impar, el valor de n se sustituye por n*3 + 1. Por ejemplo, si el argumento pasado a la función seq es 3, los valores resultantes n son 3, 10, 5, 16, 8, 4, 2, 1.
Puesto que n a veces aumenta y a veces disminuye, no hay una prueba obvia de que n alcance alguna vez el valor 1, o de que el programa vaya a terminar. Para algunos valores particulares de n, se puede probar que sí termina. Por ejemplo, si el valor de inicio es una potencia de dos, entonces el valor de n será par cada vez que se pasa por el bucle, hasta que llegue a 1. El ejemplo anterior produce dicha secuencia si se inicia con 16.
Lo díficil es preguntarse si se puede probar que este programa termina para todos los valores positivos de n. Hasta ahora, nadie ha sido capaz de probar que lo hace o ¡que no lo hace! (Vea https://es.wikipedia.org/wiki/Conjetura_de_Collatz.)
Ejercicio 7-1
Reescribe la función printn de Sección 5.8 utilizando iteración en vez de recursión.
break
A veces no se sabe que un ciclo debe terminar hasta que se llega al cuerpo. En ese caso, se puede usar la sentencia break para salir del bucle.
Por ejemplo, suponga que se desea recibir entradas del usuario hasta que este escriba "listo". Podríamos escribir:
while true
print("> ")
linea = readline()
if line == "listo"
break
end
println(linea)
end
println("¡Listo!")La condición del bucle es true, que siempre es verdadero, por lo que el bucle se ejecuta hasta que llega a la sentencia break.
En cada iteración, se le pide al usuario (con el símbolo "> ") una entrada. Si el usuario escribe listo, la sentencia break sale del bucle. De lo contrario, el programa repite lo que escriba el usuario y vuelve a la parte superior del bucle. A continuación se muestra cómo funciona este programa:
> no listo
no listo
> listo
¡Listo!Esta forma de escribir bucles while es común porque permite verificar la condición en cualquier parte del bucle (no solo en la parte superior) y puede expresar la condición de término de manera afirmativa ("detenerse cuando esto suceda"), en vez de negativamente ("continuar hasta que esto suceda").
continue
La sentencia break permite terminar el bucle. Cuando aparece una sentencia continue dentro de un bucle, se regresa al comienzo del bucle, ignorando todos las sentencias que quedan en la iteración actual del bucle e inicia la siguiente iteración. Por ejemplo:
for i in 1:10
if i % 3 == 0
continue
end
print(i, " ")
endOutput:
1 2 4 5 7 8 10
Si i es divisible por 3, la sentencia continue detiene la iteración actual y comienza la siguiente iteración. Solo se imprimen los números en el rango de 1 a 10 no divisibles por 3.
Raíces Cuadradas
Los bucles son comúnmente utilizados en programas que calculan resultados numéricos y que comienzan con una respuesta aproximada que es iterativamente mejorada.
Por ejemplo, una forma de calcular raíces cuadradas es el método de Newton. Suponga que desea conocer la raíz cuadrada de \(a\). Si comienza con casi cualquier estimación \(x\), puede calcular una mejor aproximación con la siguiente fórmula:
Por ejemplo, si \(a\) es 4 y \(x\) es 3:
julia> a = 4
4
julia> x = 3
3
julia> y = (x + a/x) / 2
2.1666666666666665El resultado está más cerca de la respuesta correcta (\(\sqrt 4 = 2\)). Si se repite el proceso con la nueva estimación, se acerca aún más:
julia> x = y
2.1666666666666665
julia> y = (x + a/x) / 2
2.0064102564102564Después de algunas actualizaciones, la estimación es casi exacta:
julia> x = y
2.0064102564102564
julia> y = (x + a/x) / 2
2.0000102400262145
julia> x = y
2.0000102400262145
julia> y = (x + a/x) / 2
2.0000000000262146En general, no se sabe de antemano cuántos pasos se necesitan para llegar a la respuesta correcta, pero se sabe que se ha llegado a ella cuando la estimación deja de cambiar:
julia> x = y
2.0000000000262146
julia> y = (x + a/x) / 2
2.0
julia> x = y
2.0
julia> y = (x + a/x) / 2
2.0Cuando y == x, ya se pueden detener los cómputos. A continuación se muestra un ciclo que comienza con una estimación inicial, x, la cual mejora hasta que deja de cambiar:
while true
println(x)
y = (x + a/x) / 2
if y == x
break
end
x = y
endPara la mayoría de los valores de a esto funciona bien, aunque en general no se recomienda probar igualdad entre números de punto flotante. Los números de punto flotante son aproximadamente correctos: la mayoría de los números racionales, como \(\frac{1}{3}\), e irracionales, como \(\sqrt 2\), no pueden ser representados exactamente con un Float64.
En lugar de verificar si x e y son exactamente iguales, es más seguro usar la función integrada abs para calcular el valor absoluto o la magnitud de la diferencia entre ellos:
if abs(y-x) < ε
break
endDonde ε (\varepsilon TAB) toma un valor como 0.0000001 que determina cómo de cerca es suficientemente cerca.
Algoritmos
El método de Newton es un ejemplo de un algoritmo, un proceso mecánico que permite resolver una categoría de problemas (en este caso, el cálculo de raíces cuadradas).
Para comprender qué es un algoritmo, podría ayudar empezar con algo que no es un algoritmo. Cuando aprendió a multiplicar números de un solo dígito, probablemente memorizó la tabla de multiplicar. En efecto, memorizó 100 soluciones específicas. Ese tipo de conocimiento no es un algoritmo.
Pero si fuera "perezoso", podría haber aprendido algunos trucos. Por ejemplo, para encontrar el producto de \(n\) y 9, puede escribir \(n-1\) como el primer dígito y \(10-n\) como el segundo dígito. Este truco es una solución general para multiplicar cualquier número de un solo dígito por 9. ¡Esto sí es un algoritmo!
Del mismo modo, las técnicas que aprendió para la suma con “llevamos tanto”, la resta con “pedimos prestado tanto”, y la división “larga o con galera o de casita” son todas ellas algoritmos. Una de las características de los algoritmos es que no requieren inteligencia para realizarlos. Son procesos mecánicos donde cada paso se sigue de acuerdo con un conjunto simple de reglas.
Ejecutar algoritmos es aburrido, pero diseñarlos es interesante, intelectualmente desafiante y constituyen una parte central de la informática.
Algunas de las cosas que las personas hacen naturalmente, sin dificultad o conscientemente, son las más difíciles de expresar en algoritmos. Comprender el lenguaje natural es un buen ejemplo. Todo el mundo lo hace, pero hasta ahora nadie ha podido explicar cómo se hace, al menos no en forma de algoritmo.
Depuración
A medida que comience a escribir programas más extensos, es posible que pase más tiempo depurando. Más código significa más posibilidades de cometer un error y más lugares dónde se pueden esconder los errores.
Una forma de reducir el tiempo de depuración es "depurar por bisección". Por ejemplo, si hay 100 líneas en su programa y las revisa una a la vez, serían 100 revisiones.
Es mejor tratar de dividir el problema en dos. Busque en la mitad del programa o un valor intermedio que pueda verificar. Agregue una sentencia de impresión (o algo que permita verificar) y ejecute el programa.
Si esta verificación es incorrecta, debe haber un problema en la primera mitad del programa. Si es correcta, el problema está en la segunda mitad.
Cada vez que realiza una verificación como esta, reduce a la mitad el número de líneas que debe revisar. Después de seis pasos (que es mucho menos que 100), se reduciría a una o dos líneas de código, al menos en teoría.
En la práctica, no siempre se conoce dónde está la "mitad del programa", y no siempre es posible verificarlo. No tiene sentido contar líneas y encontrar el punto medio exacto. En su lugar, piense en los lugares del programa donde puede haber errores y en los lugares donde es fácil verificar. Luego, elija un lugar en donde usted crea que las posibilidades de encontrar un error antes o después de esta verificación son más o menos las mismas.
Glosario
- asignación múltiple
-
Asignar un nuevo valor a una variable que ya existe.
- actualización
-
Asignación donde el nuevo valor de la variable depende del antiguo.
- inicialización
-
Asignación que le da un valor inicial a una variable que será actualizada.
- incremento
-
Actualización que incrementa el valor de la variable (usualmente en 1).
- decremento
-
Actualización que disminuye el valor de la variable (usualmente en 1).
- iteración
-
Ejecución repetida de un conjunto de sentencias, usando una función recursiva o un bucle.
- sentencia while
-
Sentencia que permite iteraciones controladas por una condición.
- sentencia break
-
Sentencia que permite salir de un bucle.
- sentencia continue
-
Sentencia localizada dentro de un bucle, que obliga a iniciar una nueva iteración desde el inicio del bucle.
- bucle infinito
-
Un bucle cuya condición de término no es satisfecha.
- algoritmo
-
Proceso general para resolver una categoría de problemas.
Ejercicios
Ejercicio 7-2
Copie el bucle de Sección 7.6 e insértelo en una función llamada miraiz que tome a como parámetro, elija un valor razonable de x y devuelva una estimación de la raíz cuadrada de a.
Para probarla, escriba una función llamada probarraiz que imprima una tabla como esta:
a mysqrt sqrt diff - ------ ---- ---- 1.0 1.0 1.0 0.0 2.0 1.414213562373095 1.4142135623730951 2.220446049250313e-16 3.0 1.7320508075688772 1.7320508075688772 0.0 4.0 2.0 2.0 0.0 5.0 2.23606797749979 2.23606797749979 0.0 6.0 2.449489742783178 2.449489742783178 0.0 7.0 2.6457513110645907 2.6457513110645907 0.0 8.0 2.82842712474619 2.8284271247461903 4.440892098500626e-16 9.0 3.0 3.0 0.0
La primera columna es un número, a; la segunda columna es la raíz cuadrada de a calculada con miraiz; la tercera columna es la raíz cuadrada calculada con la función integrada sqrt y la cuarta columna es el valor absoluto de la diferencia entre las dos estimaciones.
Exercise 7-3
La función integrada Meta.parse toma una cadena y la transforma en una expresión. Esta expresión se puede evaluar en Julia con la función Core.eval. Por ejemplo:
julia> expr = Meta.parse("1+2*3")
:(1 + 2 * 3)
julia> eval(expr)
7
julia> expr = Meta.parse("sqrt(π)")
:(sqrt(π))
julia> eval(expr)
1.7724538509055159Escriba una función llamada evalbucle que iterativamente solicite una entrada al usuario, tome la entrada resultante, la evalúe usando eval y pase posteriormente a imprimir el resultado. Debe continuar hasta que el usuario ingrese listo y luego devolver el valor de la última expresión que evaluó.
Exercise 7-4
El matemático Srinivasa Ramanujan encontró una serie infinita que puede usarse para generar una aproximación numérica de \(\frac{1}{\pi}\):
Escriba una función llamada estimarpi que utilice esta fórmula para calcular y devolver una estimación de π. Debe usar un ciclo while para calcular los términos de la suma hasta que el último término sea menor que 1e-15 (que es la notación de Julia para \(10^{-15}\)). Puede verificar el resultado comparándolo con π.
8. Cadenas
Las cadenas son diferentes de los números enteros, flotantes y booleanos. Una cadena es una secuencia, es decir, una colección ordenada de valores. En este capítulo se verá cómo acceder a los caracteres que forman una cadena y se conocerán algunas funciones integradas en Julia relacionadas con cadenas.
Caracteres
Los hispanohablantes están familiarizados con algunos caracteres, tales como las letras del alfabeto (A, B, C, …), los números y los signos de puntuación comunes. Estos caracteres están estandarizados en el código ASCII (Código Estándar Estadounidense para el Intercambio de Información).
Por supuesto hay muchos otros caracteres utilizados en idiomas distintos del español que no están en el código ASCII, tales como aquellos usados en los idiomas griego, árabe, chino, hebreo, hindi, japonés y coreano.
Definir qué es un carácter es altamente complejo. La norma Unicode permite abordar este problema, y se considera como el estándar definitivo para ello. Esta norma funciona asignando un número único para cada carácter a nivel global.
Un valor Char representa un único carácter y está entre comillas simples:
julia> 'x'
'x': ASCII/Unicode U+0078 (category Ll: Letter, lowercase)
julia> '🍌'
'🍌': Unicode U+1F34C (category So: Symbol, other)
julia> typeof('x')
CharIncluso los emojis son parte del estándar Unicode. (\:banana: TAB)
Una Cadena es una Secuencia
Una cadena es una secuencia de caracteres. Se puede acceder a un carácter con el operador corchete:
julia> fruta = "banana"
"banana"
julia> letra = fruta[1]
'b': ASCII/Unicode U+0062 (category Ll: Letter, lowercase)La segunda sentencia selecciona el carácter número 1 de fruta y la asigna a la variable letra.
La expresión entre corchetes se llama indice. El índice indica el carácter de la secuencia a obtener (de ahí el nombre).
La indexación en Julia es base 1, es decir, el primer elemento de cualquier objeto indexado con enteros está en el índice 1, y el último en el índice end:
julia> fruta[end]
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)Como índice se pueden usar expresiones que contengan variables y operadores:
julia> i = 1
1
julia> fruta[i+1]
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)
julia> fruta[end-1]
'n': ASCII/Unicode U+006E (category Ll: Letter, lowercase)No obstante, el valor del índice tiene que ser un número entero. De lo contrario se obtiene:
julia> letra = fruta[1.5]
ERROR: MethodError: no method matching getindex(::String, ::Float64)length
length es una función integrada que devuelve el número de caracteres de una cadena:
julia> frutas = "🍌 🍎 🍐"
"🍌 🍎 🍐"
julia> len = length(frutas)
5Para obtener la última letra de una cadena, puede sentirse tentado a probar algo como esto:
julia> last = frutas[len]
' ': ASCII/Unicode U+0020 (category Zs: Separator, space)Pero con esto no se obtiene el resultado esperado.
Las cadenas se codifican usando codificación UTF-8. UTF-8 es una codificación de longitud variable, lo que significa que no todos los caracteres están codificados con el mismo número de bytes.
La función sizeof devuelve el número de bytes de una cadena:
julia> sizeof("🍌")
4Dado que un emoji está codificado en 4 bytes y la indexación de cadenas está basada en bytes, el quinto elemento de frutas es un ESPACIO.
Esto significa que no todos los índices de byte de una cadena UTF-8 son necesariamente índices válidos para un carácter. Si en una cadena se indexa con un índice de bytes no válido, se genera un error:
julia> frutas[2]
ERROR: StringIndexError("🍌 🍎 🍐", 2)En el caso de frutas, el carácter 🍌 es un carácter de cuatro bytes, por lo que los índices 2, 3 y 4 no son válidos y el índice del siguiente carácter es 5, el siguiente índice válido se puede calcular con nextind(frutas, 1), el subsiguiente con nextind(frutas,5) y así sucesivamente.
Recorrido
Muchos cálculos implican procesar una cadena carácter por carácter. A menudo empiezan por el principio, seleccionan cada carácter por turno, hacen algo con él y continúan hasta el final. Este patrón de proceso se llama recorrido. Una forma de escribir un recorrido es con una sentencia while:
indice = firstindex(frutas)
while indice <= sizeof(frutas)
letra = frutas[indice]
println(letra)
global indice = nextind(frutas, indice)
endEste bucle recorre la cadena y muestra cada letra en una línea distinta. La condición del bucle es index <= sizeof(fruta), de modo que cuando el índice es mayor al número de bytes en la cadena, la condición es falsa y no se ejecuta el cuerpo del bucle.
La función firstindex devuelve el primer índice de bytes válido. La palabra reservada global antes de indice indica que queremos reasignar la variable indice definida en Main (ver Sección 11.7).
Ejercicio 8-1
Escriba una función que tome una cadena como argumento y que muestre las letras desde la última a la primera, una por línea.
Otra forma de escribir un recorrido es con un bucle for:
for letra in frutas
println(letra)
endCada vez que se recorre el bucle, se asigna a la variable letra el siguiente carácter de la cadena. El bucle continúa hasta que no quedan más caracteres.
El ejemplo siguiente muestra cómo usar la concatenación (multiplicación de cadenas) y un bucle for para generar una serie abecedaria (es decir, una serie con elementos en orden alfabético). Por ejemplo, en el libro de Robert McCloskey Make Way for Ducklings, los nombres de los patitos son Jack, Kack, Lack, Mack, Nack, Ouack, Pack, y Quack. Este bucle muestra esos nombres en orden:
prefijos = "JKLMNOPQ"
sufijo = "ack"
for letra in prefijos
println(letra * sufijo)
endOutput:
Jack Kack Lack Mack Nack Oack Pack Qack
Por supuesto, esto no es del todo correcto, porque “Ouack” y “Quack” no están correctamente escritos.
Ejercicio 8-2
Modifique este programa para solucionar este error.
Porciones de Cadenas
A la subcadena de una cadena se le llama porción. La selección de una porción es similar a la selección de un carácter:
julia> str = "Julio Cesar";
julia> str[1:5]
"Julio"El operador [n:m] devuelve la parte de la cadena desde el n-ésimo byte hasta el m-ésimo. Por lo tanto, se siguen las mismas reglas que para la indexación simple.
La palabra reservada end se puede usar para indicar al último byte de la cadena:
julia> str[7:end]
"Cesar"Si el primer índice es mayor que el segundo, el resultado es una cadena vacía, representada por dos comillas:
julia> str[8:7]
""Una cadena vacía no contiene caracteres y tiene una longitud de 0, pero aparte de eso es igual a cualquier otra cadena.
Ejercicio 8-3
Continuando este ejemplo, ¿qué cree que significa str[:]? Pruebe y verá.
Las Cadenas son Inmutables
Es tentador usar el operador [] en el lado izquierdo de una asignación con la intención de cambiar un carácter en una cadena. Por ejemplo:
julia> saludo = "¡Hola, mundo!"
"¡Hola, mundo!"
julia> saludo[3] = 'J'
ERROR: MethodError: no method matching setindex!(::String, ::Char, ::Int64)Nota del traductor: De acuerdo con la codificación de caracteres en utf-8 o latin-1, el carácter de exclamación ‘¡’, en la variable saludo ocupa dos posiciones, de ahí que la letra ‘H’ esté localizada en el índice 3.
La razón del error es que las cadenas son inmutables, lo que significa que no se puede cambiar una cadena existente. Lo máximo que se puede hacer es crear una nueva cadena que sea una variación de la original:
julia> saludo = "¡J" * saludo[4:end]
"¡Jola, mundo!"Este ejemplo concatena la apertura del signo de exclamación y una nueva primera letra a una porción de saludo. Esta operación no tiene efecto sobre la cadena original.
Interpolación de Cadenas
Construir cadenas usando concatenación puede ser un poco engorroso. Para disminuir la necesidad de las llamadas a string o multiplicaciones repetidas, Julia permite la interpolación de cadenas usando $:
julia> saludo = "¡Hola"
"¡Hola"
julia> paraquien = "mundo"
"mundo"
julia> "$saludo, $(paraquien)!"
"¡Hola, mundo!"Esto es más entendible y conveniente que la concatenación de cadenas: saludo * ", " * paraquien * "!"
La expresión inmediatamente siguiente a $ se toma como la expresión cuyo valor se va a interpolar en la cadena. Por lo tanto, puede interpolar cualquier expresión en una cadena usando paréntesis:
julia> "1 + 2 = $(1 + 2)"
"1 + 2 = 3"Búsqueda
¿Qué hace la siguiente función?
function busqueda(palabra, letra)
indice = primerindice(palabra)
while indice <= sizeof(palabra)
if palabra[indice] == letra
return indice
end
indice = nextind(palabra, indice)
end
-1
endEn cierto sentido, la función búsqueda es lo contrario del operador []. En lugar de tomar un índice y extraer el carácter correspondiente, toma un carácter y encuentra el índice donde aparece el carácter. Si el carácter no se encuentra, la función devuelve -1.
Este es el primer ejemplo de una sentencia return dentro de un bucle. Si palabra[indice] == letra, la función devuelve inmediatamente el índice, escapando del bucle prematuramente.
Si el carácter no aparece en la cadena, entonces el programa sale del bucle normalmente y devuelve -1.
Este patrón de computación se llama a veces un recorrido eureka porque tan pronto como encontramos lo que buscamos, podemos gritar “¡Eureka! ” y dejar de buscar.
Ejercicio 8-4
Modifique la función busqueda para que tenga un tercer parámetro: el índice de palabra donde debería comenzar a buscar.
Iterando y contando
El siguiente programa cuenta el número de veces que aparece la letra a en una cadena:
palabra = "banana"
contador = 0
for letra in palabra
if letra == 'a'
global contador = contador + 1
end
end
println(contador)Este programa es otro ejemplo del patrón de computación llamado conteo. La variable contador se inicializa en 0 y se incrementa cada vez que encuentra la letra a. Cuando termina el bucle, contador contiene el resultado (el número total de letras a).
Ejercicio 8-5
Coloque este código en una función llamada conteo, y generalícelo de tal manera que tome como argumentos una cadena y una letra.
Luego, vuelva a escribir la función para que, en vez de revisar toda la cadena, utilice la función busqueda de tres parámetros de la sección anterior.
Librería con cadenas
Julia tiene funciones integradas que realizan una variedad de operaciones útiles en cadenas. Por ejemplo, la función uppercase toma una cadena y devuelve una nueva cadena con todas las letras mayúsculas.
julia> uppercase("¡Hola, mundo!")
"¡HOLA, MUNDO!"Existe una función llamada findfirst que es notablemente similar a la función busqueda que escribimos:
julia> findfirst("a", "banana")
2:2La función findfirst es más general que la función creada: puede encontrar subcadenas, no solo caracteres:
julia> findfirst("na", "banana")
3:4Por defecto, findfirst empieza la búsqueda al comienzo de la cadena pero la función findnext toma un tercer argumento: el indice donde debería comenzar:
julia> findnext("na", "banana", 4)
5:6El operador ∈
El operador ∈ (\in TAB) es un operador booleano que toma un carácter y una cadena, y devuelve true si el primero aparece en el segundo:
julia> 'a' ∈ "banana" # 'a' en "banana"
truePor ejemplo, la siguiente función imprime todas las letras de palabra1 que también aparecen en palabra2:
function ambas(palabra1, palabra2)
for letra in palabra1
if letra ∈ palabra2
print(letra, " ")
end
end
endUna buena elección de nombres de variables permite que Julia se pueda leer como el español. Este bucle puede leerse como: "para (cada) letra en (la primera) palabra, si (la) letra es un elemento de (la segunda) palabra, imprima (la) letra".
Esto es lo que se obtiene si se compara "manzanas" y "naranjas":
julia> ambas("manzanas", "naranjas")
a n a n a sComparación de Cadenas
Los operadores de comparación trabajan sobre cadenas. Para ver si dos cadenas son iguales:
palabra = "Piña"
if palabra == "banana"
println("¡Tenemos bananas!")
endOtras operaciones de comparación son útiles para ordenar alfabéticamente palabras:
if palabra < "banana"
println("Su palabra, $palabra, va antes de banana.")
elseif word > "banana"
println("Su palabra, $palabra, va antes de banana.")
else
println("¡Tenemos bananas!")
endJulia no maneja las letras mayúsculas y minúsculas del mismo modo que son manejadas en cualquier lengua hablada. Todas las letras mayúsculas van antes de las letras minúsculas, según el estándar de codificación. Por lo tanto:
"Su palabra, Piña, va antes de banana."|
Observación
|
Una forma común de abordar este problema es convertir las cadenas a un formato estándar, como por ejemplo a minúsculas, antes de realizar la comparación. |
Depuración
Cuando se usan índices para recorrer los valores en una secuencia, es difícil acceder al principio y al final del recorrido. Aquí hay una función que compara dos palabras y devuelve true si una de las palabras es el reverso de la otra, pero contiene dos errores:
function espalindroma(palabra1, palabra2)
if length(palabra1) != length(palabra2)
return false
end
i = firstindex(palabra1)
j = lastindex(palabra2)
while j >= 0
j = prevind(palabra2, j)
if palabra1[i] != palabra2[j]
return false
end
i = nextind(palabra1, i)
end
true
endLa primera sentencia if verifica si las palabras tienen la misma longitud. Si no, se devuelve false inmediatamente. De lo contrario, para el resto de la función, se puede suponer que las palabras tienen la misma longitud. Este es un ejemplo del patrón guardián.
i y j son índices: i recorre palabra1 de derecha a izquierda mientras que j recorre palabra2 de izquierda a derecha. Si dos letras no coinciden, se devuelve false inmediatamente. Si el ciclo termina y todas las letras coinciden, se devuelve true.
La función lastindex devuelve el último índice de bytes válido de una cadena y prevind el índice válido anterior a un carácter.
Si se prueba esta función con las palabras "amor" y "roma", se espera el valor de retorno true, pero se obtiene false:
julia> espalindroma("amor", "roma")
falsePara depurar este tipo de error, primeramente se imprimen los valores de los índices:
espalindroma (generic function with 1 method)
Ahora, al ejecutar el programa, se obtiene más información:
julia> espalindroma("amor", "roma")
i = 1
j = 3
falseEn la primera iteración del bucle, el valor de j es 3, pero tendría que ser 4. Esto se puede solucionar trasladando la línea j = prevind (palabra2, j) al final del ciclo while.
Si se soluciona ese error y se ejecuta el programa nuevamente, se obtiene:
espalindroma (generic function with 1 method)
julia> espalindroma("amor", "roma")
i = 1
j = 4
i = 2
j = 3
i = 3
j = 2
i = 4
j = 1
i = 5
j = 0
ERROR: BoundsError: attempt to access String
at index [5]Esta vez se ha producido un BoundsError. El valor de i es 5, que está fuera del rango de la cadena "amor".
Ejercicio 8-6
Ejecute el programa en papel cambiando los valores de i y j durante cada iteración. Encuentre y arregle el segundo error en esta función.
Glosario
- secuencia
-
Una colección ordenada de valores donde cada valor se identifica mediante un índice entero.
- código ASCII
-
Código de caracteres estándar para el intercambio de información.
- norma Unicode
-
Un estándar en la industria informática para la codificación, representación y manejo consistentes de texto en la mayoría de los sistemas de escritura del mundo.
- índice
-
Un valor entero usado para seleccionar un miembro de un conjunto ordenado, como puede ser un carácter de una cadena. En Julia los índices comienzan en 1.
- codificación UTF-8
-
Una codificación de caracteres de longitud variable capaz de codificar todos los 1112064 puntos de código válidos en Unicode utilizando de uno a cuatro bytes de 8 bits.
- recorrer
-
Iterar sobre los elementos de un conjunto, realizando una operación similar en cada uno de ellos.
- porción
-
Una parte de una cadena especificada mediante un rango de índices.
- cadena vacía
-
Una cadena sin caracteres y longitud 0, representada por dos comillas.
- immutable
-
La propiedad de una secuencia que hace que a sus elementos no se les pueda asignar nuevos valores.
- interpolación de cadenas
-
El proceso de evaluar una cadena que contiene uno o más marcadores de posición, produciendo un resultado en el que los marcadores de posición se reemplazan con sus valores correspondientes.
- búsqueda
-
Un patrón de recorrido que se detiene cuando encuentra lo que está buscando.
- contador
-
Una variable utilizada para contar algo, generalmente inicializada en cero y luego incrementada.
Ejercicios
Ejercicio 8-7
Lea la documentación de las funciones relacionadas con cadenas en https://docs.julialang.org/en/v1/manual/strings/. Es posible que desee probar algunas de ellas para asegurarse de comprender cómo funcionan. strip y replace son particularmente útiles.
La documentación utiliza una sintaxis que puede ser confusa. Por ejemplo, en search(cadena::AbstractString, caracter::Chars, [comienzo::Integer]), los corchetes indican argumentos opcionales. Por lo tanto, cadena y caracter son obligatorios, pero comienzo es opcional.
Ejercicio 8-8
Hay una función integrada llamada count que es similar a la función en Sección 8.9. Lea la documentación de esta función y úsela para contar el número de letras a en "banana".
Ejercicio 8-9
Una porción de cadena puede tomar un tercer índice. El primero especifica el inicio, el tercero el final y el segundo el "tamaño del paso", es decir, el número de espacios entre caracteres sucesivos. Un tamaño de paso de 2 significa cada un caracter; 3 significa cada dos, etc.
julia> fruta = "banana"
"banana"
julia> fruta[1:2:6]
"bnn"Un tamaño de paso de -1 recorre la palabra hacia la izquierda, por lo que la porción [end:-1:1] genera una cadena invertida.
Use esto para escribir una versión de una línea de código de espalindroma de Sección 6.11.3.
Exercise 8-10
Las siguientes funciones están destinadas a verificar si una cadena contiene letras minúsculas, pero algunas de ellas son incorrectas. Para cada función, describa qué hace realmente la función (suponiendo que el parámetro es una cadena).
function cualquierminuscula1(s)
for c in s
if islowercase(c)
return true
else
return false
end
end
end
function cualquierminuscula2(s)
for c in s
if islowercase('c')
return "true"
else
return "false"
end
end
end
function cualquierminuscula3(s)
for c in s
bandera = islowercase(c)
end
flag
end
function cualquierminuscula4(s)
bandera = false
for c in s
bandera = bandera || islowercase(c)
end
flag
end
function cualquierminuscula5(s)
for c in s
if !islowercase(c)
return false
end
end
true
endExercise 8-11
Un cifrado César es una forma simple de cifrado que implica desplazar cada letra un número fijo de lugares. Desplazar una letra significa reemplazarla por otra letra que se encuentra un número fijo de posiciones más adelante en el alfabeto. Es posible desplazarse hasta el principio del abecedario si fuera necesario. De esta manera, con un desplazamiento de 3, A es D, y con un desplazamiento de 1, Z es A .
Para desplazar una palabra, desplace cada letra en la misma cantidad. Por ejemplo, con un desplazamiento de 6, "ABCDEF" es "GHIJKL" y con un desplazamiento de -6, "BCDE" es "VWXY". En la película 2001: Una odisea del espacio, la computadora de la nave se llama HAL, que es IBM desplazada por -1.
Escriba una función llamada desplazarpalabra que tome una cadena y un número entero como parámetros, y devuelva una nueva cadena que contenga las letras de la cadena original desplazadas por la cantidad dada.
|
Observación
|
Es posible que desee utilizar la función integrada Porque |
Algunos chistes ofensivos en Internet están codificados en ROT13, que es un cifrado César con desplazamiento 13. Si no se ofende fácilmente, encuentre y decodifice algunos de ellos.
9. Estudio de Caso: Juego de Palabras
Este capítulo presenta un segundo estudio de caso, que consiste en resolver puzzles buscando palabras que tengan ciertas propiedades. Por ejemplo, se buscarán palabras cuyas letras aparezcan en orden alfabético. Además, se presentará otra forma de desarrollar programas: la reducción a un problema previamente resuelto.
Leer listas de palabras
Para los ejercicios de este capítulo se necesita una lista de palabras en español. Hay muchas listas de palabras disponibles en la Web, pero la más adecuada para nuestro propósito es una de las listas de palabras recopiladas y contribuidas al dominio público por Ismael Olea (see http://olea.org/proyectos/lemarios/). Esta lista de 87900 palabras se encuentra en la página de Olea con el nombre de archivo lemario-general-del-espanol.txt. También es posible descargar una copia desde https://github.com/JuliaIntro/IntroAJulia.jl/blob/master/data/palabras.txt.
Este archivo es un archivo de texto simple, por lo que puede ser abierto con un editor de texto o leído con Julia. La función integrada open toma el nombre del archivo como parámetro y devuelve un objeto archivo que puede ser usado para la lectura del archivo.
IOStream(<file /home/travis/build/JuliaIntro/IntroAJulia.jl/src/../data/palabras.txt>)
julia> fin = open("palabras.txt")
IOStream(<file palabras.txt>)fin es un objeto archivo que puede ser utilizado como entrada y cuando se deja de utilizar, debe cerrarse con close(fin).
Julia tiene integradas varias funciones de lectura, entre ellas readline, que lee los caracteres del archivo hasta que llega a un salto de línea, devolviendo el resultado como una cadena:
julia> readline(fin)
"a"La primera palabra en esta lista particular es "a", que indica dirección, intervalo de tiempo, finalidad, entre otros.
El objeto archivo lleva registro de dónde quedó por última vez, por lo que si llama a readline nuevamente, se obtendrá la siguiente palabra:
julia> readline(fin)
"a-"La siguiente palabra es "a-", que es un prefijo que indica privación.
También se puede usar un archivo como parte de un bucle for. El siguiente programa lee palabras.txt e imprime cada palabra, una por línea:
for line in eachline("palabras.txt")
println(line)
endEjercicios
Ejercicio 9-1
Escriba un programa que lea palabras.txt e imprima solo las palabras con más de 20 caracteres (sin contar espacios en blanco).
Ejercicio 9-2
En 1927 Enrique Jardiel Poncela publicó cinco historias cortas, omitiendo en cada una de ellas una vocal. Estas historias incluyen "El Chofer Nuevo", narración escrita sin la letra a, y "Un marido sin vocación", sin la letra e. Dado que la letra e es la más frecuente del español, esto no es fácil de lograr.
De hecho, es difícil pensar oraciones que no utilicen esta letra. Intentarlo es complicado, pero con la práctica se vuelve más fácil.
Bueno, volviendo al tema importante.
Escriba una función llamada notiene_e que devuelva true si una palabra dada no tiene la letra e.
Modifique su programa de la sección anterior para que imprima solo las palabras que no tienen e, y que además calcule el porcentaje de palabras en la lista que no tengan e.
Ejercicio 9-3
Escriba una función llamada evitar que tome como argumentos una palabra y una cadena de letras prohibidas, y que devuelva true si la palabra no usa ninguna de las letras prohibidas.
Modifique su programa de la sección anterior para solicitar al usuario que ingrese una cadena de letras prohibidas, y que luego imprima el número de palabras que no contengan ninguna de ellas. ¿Es posible encontrar una combinación de 5 letras prohibidas que excluya la menor cantidad de palabras?
Ejercicio 9-4
Escriba una función llamada usasolo que tome una palabra y una cadena de letras, y que devuelva true si la palabra contiene solo letras de la lista. ¿Puede hacer una oración usando solo las letras oneacmil? Aparte de "¿El camino?"
Ejercicio 9-5
Escriba una función llamada usatodo que tome una palabra y una cadena de letras, y que devuelva true si la palabra usa todas las letras requeridas al menos una vez. ¿Cuántas palabras usan todas las vocales aeiou?
Ejercicio 9-6
Escriba una función llamada esabecedaria que devuelva true si las letras de una palabra aparecen en orden alfabético. ¿Cuántas palabras de este tipo hay?
Búsqueda
Todos los ejercicios en la sección anterior tienen algo en común: se pueden resolver con el patrón de búsqueda. El ejemplo más simple es:
function notiene_e(palabra)
for letra in palabra
if letra == 'e'
return false
end
end
true
endEl bucle for recorre los caracteres de palabra. Si encontramos la letra e, puede devolver inmediatamente false, de lo contrario hay que pasar a la siguiente letra. Si se sale del bucle normalmente, eso significa que no se encontró una e, por lo que la función devuelve true.
Esta función podría ser escrita de manera más concisa usando el operador ∉ (\notin TAB), pero se comienza con esta versión porque muestra la lógica del patrón de búsqueda.
evita es una versión más general de notiene_e pero tiene la misma estructura:
function evita(palabra, prohibidas)
for letra in palabra
if letter ∈ prohibidas
return false
end
end
true
endSe devuelve false tan pronto como se encuentre una letra prohibida, si llegamos al final del ciclo, se devuelve true.
usasolo es similar, excepto que el sentido de la condición se invierte:
function usasolo(palabra, disponibles)
for letra in palabra
if letra ∉ disponibles
return false
end
end
true
endEn vez de un conjunto de letras prohibidas, se tiene un conjunto de letras disponibles. Si se encuentra una letra en palabra que no está en disponible, se devuelve false.
usatodo es similar, excepto que se invierte el papel de la palabra y la cadena de letras:
function usatodo(palabra, requeridas)
for letra in requeridas
if letra ∉ palabra
return false
end
end
true
endEn lugar de recorrer las letras de la palabra, el bucle recorre las letras requeridas. Si alguna de las letras requeridas no aparece en la palabra, se devuelve false.
Si se pensara como un informático se reconocería que usatodo es una instancia de un problema previamente resuelto y se podría haber escrito:
function usatodo(palabra, requeridas)
usasolo(requeridas, palabra)
endEste es un ejemplo de una forma de desarrollar programas llamada reducción a un problema resuelto previamente, lo que significa que se reconoce el problema en el que se está trabajando como una instancia de un problema ya resuelto y se aplica la solución existente.
Bucle con índices
Las funciones de la sección anterior fueron escritas con ciclos for porque solo se necesitaban los caracteres en las cadenas y no hubo necesidad de trabajar con los índices.
Para esabecedaria tenemos que comparar letras adyacentes, lo cual es un poco complicado con un ciclo for:
function esabecedaria(palabra)
i = firstindex(palabra)
previa = palabra[i]
j = nextind(palabra, i)
for c in palabra[j:end]
if c < previa
return false
end
previa = c
end
true
endOtra alternativa es usar recursividad:
function esabecedaria(palabra)
if length(palabra) <= 1
return true
end
i = firstindex(palabra)
j = nextind(palabra, i)
if palabra[i] > palabra[j]
return false
end
esabecedaria(palabra[j:end])
endUna tercera opción es usar un ciclo while:
function esabecedaria(palabra)
i = firstindex(palabra)
j = nextind(palabra, 1)
while j <= sizeof(palabra)
if palabra[j] < palabra[i]
return false
end
i = j
j = nextind(palabra, i)
end
true
endEl ciclo comienza en i=1 y j=nextind(palabra, 1) y termina cuando j>sizeof(palabra). En cada iteración, se compara el carácter iésimo (que se puede considerar como el carácter actual) con el carácter jésimo (que se puede considerar como el siguiente).
Si el siguiente carácter es menor (va antes en el alfabeto) que el actual, entonces la palabra no tiene sus letras en orden alfabético, y se devuelve false.
Si se llega al final del ciclo sin encontrar letras que imposibiliten el orden alfabético, entonces la palabra pasa la prueba. Para convencerse de que el ciclo termina correctamente, considere como ejemplo la palabra "Abel".
A continuación se muestra una versión de espalindromo que usa dos índices: uno comienza al principio de la palabra y aumenta su valor, y el otro comienza al final y disminuye su valor.
function espalindromo(palabra)
i = firstindex(palabra)
j = lastindex(palabra)
while i<j
if palabra[i] != palabra[j]
return false
end
i = nextind(palabra, i)
j = prevind(palabra, j)
end
true
endO podríamos reducir este problema a uno previamente resuelto y escribir:
function espalindromo(palabra)
isreverse(palabra, palabra)
endUsando esreverso de Sección 8.13.
Depuración
Comprobar el correcto funcionamiento de los programas es difícil. Las funciones de este capítulo son relativamente fáciles de probar porque se pueden verificar los resultados a mano. Aun así, es casi imposible elegir un conjunto de palabras que permitan evaluar todos los posibles errores.
Tomando notiene_e como ejemplo, hay dos casos obvios que verificar: las palabras que tienen una e deberían devolver false y las palabras que no, deberían devolver true. No deberían haber problemas para encontrar un ejemplo de cada uno.
Dentro de cada caso, hay algunos subcasos menos obvios. Entre las palabras que tienen una "e", se deben probar las palabras con una "e" al principio, al final y al medio. Además, se deben probar palabras largas, cortas y muy cortas, como una cadena vacía. La cadena vacía es un ejemplo de un "caso especial" no obvio donde pueden originarse errores.
Además de las instancias de prueba generadas, también puede probar su programa con una lista de palabras como palabras.txt. Al escanear el resultado, es posible que pueda detectar errores, pero tenga cuidado: puede detectar un tipo de error (palabras que no deberían incluirse, pero lo están) y no otro (palabras que deberían incluirse, pero no lo están).
Por lo general, las pruebas pueden ayudarlo a encontrar errores, pero no es fácil generar un buen conjunto de instancias de prueba e incluso si lo hace, no puede estar seguro de que su programa sea correcto. Según un informático muy famoso:
Las pruebas de programa se pueden usar para mostrar la presencia de errores, ¡pero nunca para mostrar su ausencia!
Glosario
- objeto archivo o file stream
-
Un valor que representa un archivo abierto.
- reducción a un problema previamente resuelto
-
Una manera de resolver un problema expresándolo como una instancia de un problema previamente resuelto.
- caso especial
-
Una instancia de prueba que es atípica o no obvia (y por lo tanto, menos probable que se maneje correctamente).
Ejercicios
Ejercicio 9-7
Esta pregunta se basa en un Puzzle que se transmitió en el programa de radio Car Talk (https://www.cartalk.com/puzzler/browse):
Se tiene una secuencia de números y se desea saber cuál es el siguiente. Los números son: 4, 6, 12, 18, 30, 42, 60 y luego X.
Pista 1: Todos los números de la secuencia son pares. Pista 2: El número que va después del que estoy buscando es 102.
¿Cuál es el número?
Primero, piense el patrón que busca, y luego escriba un programa que le permita encontrar el número que sigue este patrón, que se encuentra entre 60 y 102.
Ejercicio 9-8
A continuación se muestra otro puzzle de Car Talk (https://www.cartalk.com/puzzler/browse):
Estaba conduciendo por la autopista el otro día y vi mi odómetro. Como la mayoría de los odómetros, muestra seis dígitos y solo en kilómetros enteros. Entonces, si mi automóvil tuviera un kilometraje de 300000, por ejemplo, sería 3-0-0-0-0-0.
Ahora, lo que vi ese día fue muy interesante. Noté que los últimos 4 dígitos eran palindrómicos; es decir, se leían igual hacia adelante que hacia atrás. Por ejemplo, 5-4-4-5 es un palíndromo, por lo que mi odómetro podría haberse leído 3-1-5-4-4-5.
Un kilómetro después, los últimos 5 números fueron palindrómicos. Por ejemplo, podría haberse leído 3-6-5-4-5-6. Un kilómetro después de eso, los 4 números del medio eran palindrómicos. ¿Y… estás listo para esto? ¡Un kilómetro después, los 6 eran palindrómicos!
La pregunta es, ¿qué número estaba en el odómetro cuando miré por primera vez?
Escriba un programa de Julia que pruebe todos los números de seis dígitos e imprima cualquier número que satisfaga estos requisitos.
Ejercicio 9-9
Aquí hay otro puzzle de Car Talk que puede resolver con una búsqueda (https://www.cartalk.com/puzzler/browse):
Hace poco visité a mi madre y nos dimos cuenta de que los dos dígitos que componen mi edad cuando se invertían daban como resultado su edad. Por ejemplo, si tiene 73 años, yo tengo 37. Nos preguntamos con qué frecuencia esto ha sucedido a lo largo de los años, pero nos desviamos de otros temas y nunca obtuvimos una respuesta.
Cuando llegué a casa descubrí que los dígitos de nuestras edades han sido reversibles seis veces hasta ahora. También descubrí que si teníamos suerte, volvería a suceder en unos años, y si tenemos mucha suerte, sucedería una vez más después de eso. En otras palabras, habría sucedido 8 veces. Entonces la pregunta es, ¿cuántos años tengo ahora?
Escriba un programa de Julia que busque soluciones para este puzzle.
|
Observación
|
Puede encontrar la función |
10. Arreglos
Este capítulo presenta uno de los tipos más útiles de Julia: los arreglos. También se tratarán objetos y lo que puede suceder cuando se tiene más de un nombre para el mismo objeto.
Un arreglo es una secuencia
Al igual que una cadena de texto, un arreglo es una secuencia de valores. En una cadena los valores son caracteres, en un arreglo pueden ser de cualquier tipo. Los valores en un arreglo se denominan elementos o, a veces, items.
Hay varias formas de crear un nuevo arreglo, la más sencilla es encerrar los elementos entre corchetes ([ ]):
[10, 20, 30, 40]
["abadejo", "falsía", "estrambote"]El primer ejemplo es un arreglo de cuatro enteros. El segundo es un arreglo de tres cadenas de texto. Los elementos de un arreglo no tienen por qué ser del mismo tipo. El siguiente arreglo contiene una cadena, un número de punto flotante, un entero y otro arreglo:
["spam", 2.0, 5, [10, 20]]Se dice que un arreglo dentro de otro arreglo está anidado.
Un arreglo que no contiene elementos se llama arreglo vacío y se puede crear uno con corchetes vacíos, [].
Como es de esperar, se pueden asignar valores de arreglos a variables:
julia> quesos = ["Cheddar", "Edam", "Gouda"];
julia> numeros = [42, 123];
julia> vacio = [];
julia> print(quesos, " ", numeros, " ", vacio)
["Cheddar", "Edam", "Gouda"] [42, 123] Any[]La función typeof se puede usar para conocer el tipo del arreglo:
julia> typeof(quesos)
Array{String,1}
julia> typeof(numeros)
Array{Int64,1}
julia> typeof(vacio)
Array{Any,1}El tipo del arreglo se especifica entre llaves, y se compone de un tipo y un número. El número indica las dimensiones. El conjunto vacío contiene valores de tipo Any, es decir, puede contener valores de todos los tipos.
Los arreglos son mutables
La sintaxis para acceder a los elementos de un arreglo es el mismo que para acceder a los caracteres de una cadena: el operador corchete. La expresión dentro de los corchetes especifica el índice. Recuerde que los índices comienzan en 1:
julia> quesos[1]
"Cheddar"A diferencia de las cadenas, los arreglos son mutables, lo que significa que podemos cambiar sus elementos. Se puede modificar uno de sus elementos usando el operador corchetes en el lado izquierdo de una asignación:
julia> numeros[2] = 5
5
julia> print(numeros)
[42, 5]El segundo elemento de numeros, que era 123, ahora es 5.
Figura 11 muestra los diagramas de estado para quesos, numeros y vacio.
Los arreglos son representados mediante cuadros con elementos del arreglo en su interior. El arreglo quesos hace referencia a un arreglo con tres elementos indexados 1, 2 y 3. El arreglo numeros contiene dos elementos. El diagrama muestra que el valor del segundo elemento de numeros se ha reasignado de 123 a 5. Finalmente, vacio hace referencia a un arreglo sin elementos.
Los índices de un arreglo funcionan de la misma manera que los índices de una cadena (pero sin los problemas generados por la codificación UTF-8):
-
Cualquier expresión entera se puede usar como índice.
-
Si se intenta leer o escribir un elemento que no existe, se obtiene un
BoundsError. -
La palabra reservada
endindica el último índice del arreglo.
El operador ∈ también funciona en arreglos:
julia> "Edam" ∈ quesos
true
julia> "Brie" in quesos
falseRecorriendo un Arreglo
La forma más común de recorrer los elementos de un arreglo es con un ciclo for. La sintaxis es la misma que para las cadenas:
for queso in quesos
println(queso)
endEsto funciona bien si solo se necesita leer los elementos del arreglo, pero si se desea escribir o actualizar los elementos es necesario utilizar índices. Una forma común de hacerlo es usando la función integrada eachindex:
for i in eachindex(numeros)
numeros[i] = numeros[i] * 2
endEste bucle recorre el arreglo y actualiza cada elemento. En cada iteración del ciclo, i representa el índice del elemento actual. La sentencia de asignación usa numeros[i] para leer el valor original del elemento y asignar el nuevo valor.
Por otra parte, length devuelve el número de elementos en el arreglo.
Un ciclo for sobre un arreglo vacío nunca ejecuta el cuerpo del bucle:
for x in []
println("Esto nunca pasa.")
endAunque un arreglo puede contener otro arreglo, este arreglo anidado cuenta como un elemento único. Por ejemplo, la longitud de este arreglo es cuatro:
["spam", 1, ["Brie", "Roquefort", "Camembert"], [1, 2, 3]]Porciones de arreglos
El operador porción también funciona en arreglos:
julia> t = ['a', 'b', 'c', 'd', 'e', 'f'];
julia> print(t[1:3])
['a', 'b', 'c']
julia> print(t[3:end])
['c', 'd', 'e', 'f']El operador porción [:] hace una copia de todo el arreglo:
julia> print(t[:])
['a', 'b', 'c', 'd', 'e', 'f']Como los arreglos son mutables, es útil hacer una copia antes de realizar operaciones que las modifiquen.
Un operador porción en el lado izquierdo de una asignación puede actualizar varios elementos:
julia> t[2:3] = ['x', 'y'];
julia> print(t)
['a', 'x', 'y', 'd', 'e', 'f']Librería de Arreglos
Julia tiene funciones integradas que operan en arreglos. Por ejemplo, push! agrega un nuevo elemento al final de un arreglo:
julia> t = ['a', 'b', 'c'];
julia> push!(t, 'd');
julia> print(t)
['a', 'b', 'c', 'd']append! agrega elementos de un arreglo al final de otro:
julia> t1 = ['a', 'b', 'c'];
julia> t2 = ['d', 'e'];
julia> append!(t1, t2);
julia> print(t1)
['a', 'b', 'c', 'd', 'e']En este ejemplo t2 no es modificado.
sort! ordena los elementos de un arreglo de menor a mayor:
julia> t = ['d', 'c', 'e', 'b', 'a'];
julia> sort!(t);
julia> print(t)
['a', 'b', 'c', 'd', 'e']sort devuelve una copia ordenada de los elementos de un arreglo:
julia> t1 = ['d', 'c', 'e', 'b', 'a'];
julia> t2 = sort(t1);
julia> print(t1)
['d', 'c', 'e', 'b', 'a']
julia> print(t2)
['a', 'b', 'c', 'd', 'e']|
Nota
|
Como convención en Julia, se agrega |
Mapear, Filtrar y Reducir
Para sumar todos los números en un arreglo se puede usar un ciclo como este:
function sumartodo(t)
total = 0
for x in t
total += x
end
total
endtotal se inicializa en 0. En cada iteración, con += se añade un elemento del arreglo a la suma total. El operador += es una forma simple de actualizar esta variable. Esta sentencia de asignación aumentada,
total += xes equivalente a
total = total + xA medida que se ejecuta el ciclo, total acumula la suma de los elementos. A veces se denomina acumulador a una variable utilizada de esta manera.
Sumar los elementos de un arreglo es una operación tan común que Julia tiene una función integrada para ello, sum:
julia> t = [1, 2, 3, 4];
julia> sum(t)
10Una operación como esta, que combina una secuencia de elementos en un solo valor, a veces se denomina operación de reducción.
Es común querer recorrer un arreglo mientras se construye otro. Por ejemplo, la siguiente función toma un arreglo de cadenas y devuelve un nuevo arreglo que contiene las mismas cadenas pero en mayúsculas:
function todoenmayusculas(t)
res = []
for s in t
push!(res, uppercase(s))
end
res
endres se inicializa con un arreglo vacío, y en cada iteración se le agrega un nuevo elemento. De esta manera, res es otro tipo de acumulador.
Una operación como todoenmayusculas a veces se denomina mapeo porque "asigna" una función (en este caso uppercase) a cada uno de los elementos de una secuencia.
Otra operación común es seleccionar solo algunos de los elementos de un arreglo y devolver una sub-arreglo. Por ejemplo, la siguiente función toma un arreglo de cadenas y devuelve un arreglo que contiene solamente las cadenas en mayúsculas:
function solomayusculas(t)
res = []
for s in t
if s == uppercase(s)
push!(res, s)
end
end
res
endOperaciones como solomayusculas se llaman filtro porque seleccionan solo algunos elementos, filtrando otros.
Las operaciones de arreglos más comunes son una combinación de mapeo, filtro y reducción.
Sintaxis de punto
Para cada operador binario, como por ejemplo ^, existe un operador punto correspondiente .^ que automáticamente define la operación ^ para cada elemento de un arreglo. Por ejemplo, [1, 2, 3] ^ 3 no está definido, pero [1, 2, 3] .^ 3 se define como el resultado de realizar la operación ^ en cada elemento [1^3, 2^3, 3^3]:
julia> print([1, 2, 3] .^ 3)
[1, 8, 27]Cualquier función f de Julia puede ser aplicada a cada elemento de cualquier arreglo con la sintaxis de punto. Por ejemplo, para poner en mayúsculas un arreglo de cadenas, no es necesario un bucle explícito:
julia> t = uppercase.(["abc", "def", "ghi"]);
julia> print(t)
["ABC", "DEF", "GHI"]Esta es una forma elegante de crear un mapeo. Siguiendo esta lógica, la función todoenmayusculas puede implementarse con una línea:
function todoenmayusculas(t)
uppercase.(t)
endBorrando (Insertando) Elementos
Hay varias formas de eliminar elementos de un arreglo. Si se conoce el índice del elemento que se desea eliminar, se puede usar splice!:
julia> t = ['a', 'b', 'c'];
julia> splice!(t, 2)
'b': ASCII/Unicode U+0062 (category Ll: Letter, lowercase)
julia> print(t)
['a', 'c']splice! modifica el arreglo y devuelve el elemento que se eliminó.
pop! elimina y devuelve el último elemento:
julia> t = ['a', 'b', 'c'];
julia> pop!(t)
'c': ASCII/Unicode U+0063 (category Ll: Letter, lowercase)
julia> print(t)
['a', 'b']popfirst! elimina y devuelve el primer elemento:
julia> t = ['a', 'b', 'c'];
julia> popfirst!(t)
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)
julia> print(t)
['b', 'c']Las funciones pushfirst! y push! insertan un elemento al principio y al final del arreglo, respectivamente.
Si no se necesita el valor eliminado, se puede usar la función deleteat!:
julia> t = ['a', 'b', 'c'];
julia> print(deleteat!(t, 2))
['a', 'c']La función insert! inserta un elemento en un índice dado:
julia> t = ['a', 'b', 'c'];
julia> print(insert!(t, 2, 'x'))
['a', 'x', 'b', 'c']Arreglos y Cadenas
Una cadena es una secuencia de caracteres y un arreglo es una secuencia de valores, pero un arreglo de caracteres no es lo mismo que una cadena. Para convertir una cadena a un arreglo de caracteres, se puede usar la función collect:
julia> t = collect("spam");
julia> print(t)
['s', 'p', 'a', 'm']La función collect divide una cadena u otra secuencia en elementos individuales.
Si desea dividir una cadena en palabras, puede usar la función split:
julia> t = split("En un lugar de la Mancha");
julia> print(t)
SubString{String}["En", "un", "lugar", "de", "la", "Mancha"]Un argumento opcional llamado delimitador especifica qué caracteres usar como límites de palabra. El siguiente ejemplo usa un guión como delimitador:
julia> t = split("hola-hola-hola", '-');
julia> print(t)
SubString{String}["hola", "hola", "hola"]join es el inverso de split. Toma un arreglo de cadenas y concatena los elementos:
julia> t = ["En", "un", "lugar", "de", "la", "Mancha"];
julia> s = join(t, ' ')
"En un lugar de la Mancha"En este caso, el delimitador es un carácter de espacio en blanco. Para concatenar cadenas sin espacios, no especifique un delimitador.
Objeto y Valores
Un objeto es algo a lo que una variable puede referirse. Hasta ahora, podría usar "objeto" y "valor" indistintamente.
Si ejecutamos estas sentencias de asignación:
a = "banana"
b = "banana"Se sabe que a y b apuntan a una cadena, pero no se sabe si están apuntando a la misma cadena. Hay dos estados posibles, los cuales se muestran en la Figura 10-2.
En un caso, a y b se refieren a dos objetos diferentes que tienen el mismo valor. En el segundo caso, se refieren al mismo objeto.
Para verificar si dos variables se refieren al mismo objeto, se puede usar el operador ≡ (\equiv TAB)) o ===.
julia> a = "banana"
"banana"
julia> b = "banana"
"banana"
julia> a ≡ b
trueEn este ejemplo, Julia solo creó un objeto de cadena, y ambas variables a y b apuntan a ella. Pero cuando se crean dos arreglos, se obtienen dos objetos:
julia> a = [1, 2, 3];
julia> b = [1, 2, 3];
julia> a ≡ b
falseEntonces el diagrama de estado se ve así Figura 13.
En este caso, se podría decir que los dos arreglos son equivalentes, porque tienen los mismos elementos, pero no idénticos, ya que no son el mismo objeto. Si dos objetos son idénticos, también son equivalentes, pero si son equivalentes, no son necesariamente idénticos.
Para ser precisos, un objeto tiene un valor. Si se evalúa [1, 2, 3], se obtendrá un objeto arreglo cuyo valor es una secuencia de enteros. Si otro arreglo tiene los mismos elementos, se dice que tiene el mismo valor, pero no es el mismo objeto.
Alias (poner sobrenombres)
Si a apunta a un objeto, y se asigna b = a, entonces ambas variables se refieren al mismo objeto:
julia> a = [1, 2, 3];
julia> b = a;
julia> b ≡ a
trueEl diagrama de estado sería como este Figura 14.
La asociación de una variable con un objeto se llama referencia. En este ejemplo, hay dos referencias al mismo objeto.
Un objeto con más de una referencia tiene más de un nombre, por lo que decimos que el objeto tiene un alias.
Si el objeto con alias es mutable, los cambios hechos a un alias afectan al otro:
julia> b[1] = 42
42
julia> print(a)
[42, 2, 3]|
Aviso
|
Aunque este comportamiento puede ser útil, a veces puede inducir a errores. En general, es más seguro evitar los alias cuando se trabaje con objetos mutables. |
No hay problema con los alias al trabajar con objetos inmutables, tales como cadenas de texto. En este ejemplo:
a = "banana"
b = "banana"Casi nunca es relevante que a y b se refieran a la misma cadena o no.
Arreglos como argumentos
Cuando se pasa un arreglo como argumento de una función, en realidad se pasa una referencia a ella. Si la función modifica el arreglo, el que hizo la llamada verá el cambio. Por ejemplo, la función borrarprimero elimina el primer elemento de un arreglo:
function borrarprimero!(t)
popfirst!(t)
endAquí se aprecia el uso de borrarprimero!:
julia> letras = ['a', 'b', 'c'];
julia> borrarprimero!(letras);
julia> print(letras)
['b', 'c']El parámetro t y la variable letras son alias de un mismo objeto. El diagrama de estado es así Figura 15.
Como el arreglo está compartido por dos marcos, se dibuja entre ambos.
Es importante distinguir entre operaciones que modifiquen arreglos y operaciones que creen nuevas arreglos. Por ejemplo, push! modifica un arreglo, pero vcat crea un nuevo arreglo.
Aquí hay un ejemplo de push!:
julia> t1 = [1, 2];
julia> t2 = push!(t1, 3);
julia> print(t1)
[1, 2, 3]t2 es un alias de t1.
Aquí hay un ejemplo de vcat:
julia> t3 = vcat(t1, [4]);
julia> print(t1)
[1, 2, 3]
julia> print(t3)
[1, 2, 3, 4]El resultado de vcat es un nuevo arreglo. El arreglo original no ha sufrido cambios.
Esta diferencia es importante al momento de escribir funciones que modifican arreglos.
Por ejemplo, esta función no elimina el primer elemento de un arrreglo:
function noborrarprimero(t)
t = t[2:end] # MALO!
endEl operador porción crea un nuevo arreglo y la asignación hace que t se refiera a ella, pero eso no afecta al arreglo t fuera de la función.
julia> t4 = noborrarprimero(t3);
julia> print(t3)
[1, 2, 3, 4]
julia> print(t4)
[2, 3, 4]Al comienzo de noborrarprimero, t y t3 se refieren al mismo arreglo. Al final, t se refiere a un nuevo arreglo, pero t3 todavía se refiere al arreglo original no modificado.
Una alternativa es escribir una función que cree y devuelva un nuevo arreglo. Por ejemplo, la función cola devuelve todos menos el primer elemento de un arreglo:
function cola(t)
t[2:end]
endEsta función no modifica el arreglo original, y se usa de la siguiente manera:
julia> letras = ['a', 'b', 'c'];
julia> demas = cola(letras);
julia> print(demas)
['b', 'c']Depuración
Un uso inadecuado de los arreglos (y otros objetos mutables) puede llevar a largas horas de depuración. A continuación se muestran algunos errores comunes y cómo evitarlos:
-
La mayoría de las funciones que operan en arreglos modifican el argumento. Esto es lo opuesto a lo que ocurre en las funciones que operan en cadenas de texto, que devuelven una nueva cadena y dejan la original sin modificaciones.
Si está acostumbrado a escribir código con cadenas de texto como este:
nueva_palabra = strip(palabra)Puede parecer tentador escribir código con arreglos como este:
t2 = sort!(t1)Pero como
sort!devuelve el arreglo originalt1modificado,t2es un alias det1.ObservaciónAntes de utilizar funciones y operadores de arreglos, debe leer la documentación detenidamente y luego probarla en modo interactivo.
-
Escoja una expresión y quédese con ella.
Parte del problema con los arreglos es que hay demasiadas formas de hacer las cosas. Por ejemplo, para eliminar un elemento de un arreglo se puede usar
pop!,popfirst!,delete_at, o incluso una asignación de porción. Para agregar un elemento se puede usarpush!,pushfirst!,insert!orvcat. Suponiendo quetes un arreglo yx, es un elemento, estas formas son correctas:insert!(t, 4, x) push!(t, x) append!(t, [x])Y estas incorrectas:
insert!(t, 4, [x]) # MALO! push!(t, [x]) # MALO! vcat(t, [x]) # MALO! -
Haga copias para evitar usar alias.
Si se desea utilizar una función como
sort!que modifica el argumento pero también se necesita mantener el arreglo original, es posible hacer una copia:julia> t = [3, 1, 2]; julia> t2 = t[:]; # t2 = copy(t) julia> sort!(t2); julia> print(t) [3, 1, 2] julia> print(t2) [1, 2, 3]En este ejemplo, también podría usar la función incorporada
sort, que devuelve un nuevo arreglo ordenado y no modifica el original:julia> t2 = sort(t); julia> println(t) [3, 1, 2] julia> println(t2) [1, 2, 3]
Glosario
- arreglo
-
Una secuencia de valores.
- elemento
-
Uno de los valores de un arreglo (u otra secuencia), también llamado ítem.
- lista anidada
-
Un arreglo que es elemento de otro arreglo.
- acumulador
-
Una variable utilizada en un ciclo para sumar o acumular un resultado.
- asignación aumentada
-
Una sentencia que actualiza el valor de una variable usando un operador como
+=. - operador punto
-
Operador binario que se aplica a cada elemento de un arreglo.
- sintaxis de punto
-
Sintaxis utilizada para aplicar una función a todos los elementos de cualquier arreglo.
- operación de reducción
-
Un patrón de procesamiento que recorre una secuencia y acumula los elementos en un solo resultado.
- mapeo
-
Un patrón de procesamiento que recorre una secuencia y realiza una operación en cada elemento.
- filtro
-
Un patrón de procesamiento que recorre una secuencia y selecciona los elementos que satisfacen algún criterio.
- objeto
-
Una cosa a la que se puede referir una variable. Un objeto tiene tipo y valor.
- equivalente
-
Tener el mismo valor.
- idéntico
-
Ser el mismo objeto (lo que implica equivalencia).
- referencia
-
La asociación entre una variable y su valor.
- alias
-
Múltiples variables que contienen referencias al mismo objeto.
- argumentos opcionales
-
Argumentos que no son necesarios.
- delimitador
-
Un carácter o cadena utilizado para indicar donde debe cortarse una cadena.
Ejercicios
estaordenada (generic function with 1 method)
Ejercicio 10-1
Escriba una función llamada sumaanidada que tome un arreglo de arreglos de enteros y sume los elementos de todos los arreglos anidados. Por ejemplo:
julia> t = [[1, 2], [3], [4, 5, 6]];
julia> sumaanidada(t)
21Ejercicio 10-2
Escriba una función llamada sumaacumulada que tome un arreglo de números y devuelva la suma acumulativa, es decir, un nuevo arreglo donde el \(i\)ésimo elemento es la suma de los primeros \(i\) elementos del arreglo original. Por ejemplo:
julia> t = [1, 2, 3];
julia> print(sumaacumulada(t))
Any[1, 3, 6]Ejercicio 10-3
Escriba una función llamada interior que tome un arreglo y devuelva un nuevo arreglo que contenga todos los elementos excepto el primero y el último. Por ejemplo:
julia> t = [1, 2, 3, 4];
julia> print(interior(t))
[2, 3]Ejercicio 10-4
Escriba una función llamada interior! que tome un arreglo, lo modifique eliminando el primer y el último elemento, y que no devuelva un valor. Por ejemplo:
julia> t = [1, 2, 3, 4];
julia> interior!(t)
julia> print(t)
[2, 3]Ejercicio 10-5
Escriba una función llamada estaordenada que tome un arreglo como parámetro y devuelva true si el arreglo se ordena en orden ascendente y false de lo contrario. Por ejemplo:
julia> estaordenada([1, 2, 2])
true
julia> estaordenada(['b', 'a'])
falseEjercicio 10-6
Dos palabras son anagramas si se pueden ordenar las letras de una para escribir la otra. Escriba una función llamada esanagrama que tome dos cadenas y devuelva true si son anagramas.
Ejercicio 10-7
Escriba una función llamada repetido que tome un arreglo y devuelva true si hay algún elemento que aparece más de una vez. No debe modificar el arreglo original.
Ejercicio 10-8
Este ejercicio se relaciona con la llamada paradoja del cumpleaños, sobre la cual puede leer en https://es.wikipedia.org/wiki/Paradoja_del_cumplea%C3%B1os
Si hay 23 estudiantes en su clase, ¿cuáles son las posibilidades de que dos de ustedes tengan el mismo cumpleaños? Puede estimar esta probabilidad generando muestras aleatorias de 23 cumpleaños y buscando coincidencias.
|
Observación
|
Puede generar cumpleaños aleatorios con |
Ejercicio 10-9
Escriba una función que lea el archivo palabras.txt y construya un arreglo con un elemento por palabra. Escriba dos versiones de esta función, una con push! y la otra con la expresión t = [t..., x]. ¿Cuál tarda más en ejecutarse? ¿Por qué?
Ejercicio 10-10
Para verificar si una palabra está en el arreglo de palabras se puede usar el operador ∈. Esto sería lento pues este operador busca las palabras en orden.
Debido a que las palabras están en orden alfabético, se puede acelerar la verificación con una búsqueda de bisección (también conocida como búsqueda binaria), que es similar a lo que se hace cuando se busca una palabra en el diccionario. Se comienza en el medio y se verifica si la palabra que se está buscando va antes que la palabra localizada en el medio. Si es así, se busca en la primera mitad de la matriz de la misma manera. De lo contrario, se busca en la segunda mitad.
En ambos casos se reduce el espacio de búsqueda restante a la mitad. Si el arreglo de palabras tiene 113,809 palabras, se necesitarán unos 17 pasos para encontrar la palabra o concluir que no está allí.
Escriba una función llamada enbiseccion que tome un arreglo ordenado y un valor objetivo, y devuelva true si la palabra está en el arreglo y false si no lo está.
Ejercicio 10-11
Dos palabras son un "par inverso" si cada una es la inversa de la otra. Escriba un programa llamado parinverso que encuentre todos los pares inversos en el arreglo de palabras.
Ejercicio 10-12
Dos palabras se "entrelazan" si al tomar letras alternando entre cada palabra se forma una nueva palabra. Por ejemplo, "pi" y "as" se entrelazan para formar "pais".
Crédito: Este ejercicio está inspirado en un ejemplo de http://puzzlers.org.
-
Escriba un programa que encuentre todos los pares de palabras que se entrelazan.
Observación¡No enumere todos los pares!
-
¿Puede encontrar tres palabras que se entrelacen, es decir, cada tercera letra forma una palabra, empezando de la primera, segunda o tercera letra de la palabra?
11. Diccionarios
Este capítulo presenta otro tipo integrado llamado diccionario.
Un Diccionario es un Mapeo
Un diccionario es como una matriz pero más general. En una matriz, los índices tienen que ser enteros; en un diccionario pueden ser (casi) de cualquier tipo.
Un diccionario contiene una colección de índices, llamados claves, y una colección de valores. Cada clave está asociada a un solo valor. La asociación entre una clave y un valor se denomina par clave-valor o, a veces, item.
En lenguaje matemático, un diccionario representa un mapeo de las claves a los valores, es decir, cada clave apunta a un valor. A modo de ejemplo, se crea un diccionario que asocia palabras en español con palabras en inglés. En este diccionario, las claves y los valores son cadenas.
La función Dict crea un nuevo diccionario sin elementos. Como Dict es el nombre de una función integrada de Julia, debe evitar usarla como nombre de variable.
julia> ing_a_esp = Dict()
Dict{Any,Any}()El tipo de este diccionario está compuesto por el tipo de las claves y de los valores, entre llaves. En este caso, las claves y los valores son de tipo Any.
El diccionario está vacío. Para agregar elementos a él, se pueden usar corchetes:
julia> ing_a_esp["one"] = "uno";Esta línea de código crea un elemento con la clave "one" que apunta al valor "uno". Si se imprime el diccionario nuevamente, se ve un par clave-valor con una flecha => entre la clave y el valor:
julia> ing_a_esp
Dict{Any,Any} with 1 entry:
"one" => "uno"Este formato de salida también es un formato de entrada. Por ejemplo, se puede crear un nuevo diccionario con tres ítems de la siguiente manera:
julia> ing_a_esp = Dict("one" => "uno", "two" => "dos", "three" => "tres")
Dict{String,String} with 3 entries:
"two" => "dos"
"one" => "uno"
"three" => "tres"Todas las claves y valores iniciales son cadenas, por lo que se crea un Dict{String,String}.
|
Aviso
|
El orden de los pares clave-valor podría no ser el mismo. Si escribe el mismo ejemplo en su computadora, podría obtener un resultado diferente. En general, el orden de los elementos en un diccionario es impredecible. |
Esto no significa un problema ya que los elementos de un diccionario nunca se indexan con índices enteros. En lugar de ello, se utilizan las claves para buscar los valores correspondientes:
julia> ing_a_esp["two"]
"dos"La clave "two" da el valor "dos", así que el orden de los ítems no importa.
Si la clave no está en el diccionario, se da un mensaje de error:
julia> ing_a_esp["four"]
ERROR: KeyError: key "four" not foundLa función length también funciona con diccionarios y devuelve el número de pares clave-valor:
julia> length(ing_a_esp)
3La función keys devuelve una colección con las claves del diccionario:
julia> ks = keys(ing_a_esp);
julia> print(ks)
["two", "one", "three"]También se puede usar el operador ∈ para ver si algo es una clave en un diccionario:
julia> "one" ∈ ks
true
julia> "uno" ∈ ks
falsePara ver si algo es un valor en un diccionario, se puede usar la función values, que devuelve una colección de valores, y luego usar el operador ∈:
julia> vs = values(ing_a_esp);
julia> "uno" ∈ vs
trueEl operador ∈ utiliza diferentes algoritmos para matrices y diccionarios. Para las matrices, busca los elementos de la matriz en orden, como en Sección 8.8. El tiempo de búsqueda es directamente proporcional al largo de la matriz.
Para los diccionarios, Julia usa un algoritmo llamado tabla hash que tiene una propiedad importante: el operador ∈ toma aproximadamente la misma cantidad de tiempo sin importar cuántos elementos haya en el diccionario.
Diccionario como una Colección de Frecuencias
Suponga que tiene una cadena y desea contar cuántas veces aparece cada letra. Hay varias formas de hacerlo:
-
Podría crear 27 variables, una para cada letra del alfabeto. Luego, recorrer la cadena y, para cada carácter, incrementar el contador correspondiente, probablemente utilizando condiciones encadenadas.
-
Podría crear una matriz con 27 elementos. Luego, podría convertir cada carácter en un número (usando la función integrada
Int), usar el número como índice en la matriz e incrementar el contador apropiado. -
Puede crear un diccionario con caracteres como claves y contadores como los valores correspondientes. La primera vez que vea un carácter, agregaría un elemento al diccionario. Después de eso, incrementaría el valor de un elemento existente.
Cada una de estas opciones realiza el mismo cálculo, pero la implementación es diferente.
Una implementación es una forma de realizar un cálculo. Algunas implementaciones son mejores que otras, por ejemplo, una ventaja de la implementación del diccionario es que no hace falta saber de antemano qué letras aparecen en la cadena y solo hay que agregar las letras que aparecen.
Así es como se vería el código:
function histograma(s)
d = Dict()
for c in s
if c ∉ keys(d)
d[c] = 1
else
d[c] += 1
end
end
d
endLa función se llama histograma, que es un término en estadística para una colección de frecuencias (o conteos).
La primera línea de la función crea un diccionario vacío. El ciclo for recorre la cadena s. En cada iteración de este ciclo, si el carácter c no está en el diccionario, se crea un nuevo elemento con la clave c y el valor inicial 1 (ya que hemos visto esta letra una vez). Si c ya está en el diccionario, se incrementa d[c].
Así es como funciona:
julia> h = histograma("brontosaurus")
Dict{Any,Any} with 8 entries:
'n' => 1
's' => 2
'a' => 1
'r' => 2
't' => 1
'o' => 2
'u' => 2
'b' => 1El histograma indica que las letras a y b aparecen una vez, o aparece dos veces, y así sucesivamente.
Los diccionarios tienen una función llamada get que toma como argumentos un diccionario, una clave y un valor predeterminado. Si la clave aparece en el diccionario, get devuelve el valor correspondiente; de lo contrario, devuelve el valor predeterminado. Por ejemplo:
julia> h = histograma("a")
Dict{Any,Any} with 1 entry:
'a' => 1
julia> get(h, 'a', 0)
1
julia> get(h, 'b', 0)
0Ejercicio 11-1
Use get para escribir la función histograma de manera más concisa. Debería poder eliminar la declaración if.
Iteración y Diccionarios
Es posible recorrer las claves del diccionario con un ciclo for. Por ejemplo, imprimirhist imprime cada clave y su valor correspondiente:
function imprimirhist(h)
for c in keys(h)
println(c, " ", h[c])
end
endAsí es como se ve la salida:
julia> h = histograma("perros");
julia> imprimirhist(h)
s 1
e 1
p 1
r 2
o 1Nuevamente, las claves no están en un orden particular. Para recorrer las claves en orden, puede usar sort y collect:
julia> for c in sort(collect(keys(h)))
println(c, " ", h[c])
end
e 1
o 1
p 1
r 2
s 1Búsqueda inversa
Dado un diccionario d y una clave k, es fácil encontrar el valor correspondiente v = d[k]. Esta operación se llama búsqueda.
Pero, ¿qué pasa si se tiene v y se quiere encontrar k? Existen dos problemas: primeramente, puede haber más de una clave que apunta al valor v. Dependiendo de lo que se quiera, es posible que se pueda elegir una de estas claves, o que se tenga que hacer una matriz que las contenga a todas. En segundo lugar, no hay una sintaxis simple para hacer una búsqueda inversa; solo se debe buscar.
A continuación se muestra una función que toma un valor y que devuelve la primera clave que apunta a ese valor:
function busquedainversa(d, v)
for k in keys(d)
if d[k] == v
return k
end
end
error("Error de Busqueda")
endEsta función es otro ejemplo del patrón de búsqueda, pero utiliza una función que no hemos visto antes: error. La función error se usa para producir un ErrorException que interrumpe el flujo normal. En este caso tiene el mensaje "Error de Busqueda", que indica que no existe una clave.
Si llega al final del ciclo, eso significa que v no aparece en el diccionario como un valor, por lo que se produce una excepción.
A continuación se muestra un ejemplo de una búsqueda inversa exitosa:
julia> h = histograma("perros");
julia> key = busquedainversa(h, 2)
'r': ASCII/Unicode U+0072 (category Ll: Letter, lowercase)y una no exitosa:
julia> key = busquedainversa(h, 3)
ERROR: Error de BusquedaEl efecto cuando generamos una excepción es el mismo que cuando Julia genera una: se imprime un trazado inverso y un mensaje de error.
Julia proporciona una forma optimizada de hacer una búsqueda inversa: findall(isequal(3),h).
|
Aviso
|
Una búsqueda inversa es mucho más lenta que una búsqueda directa. Si tiene que hacer búsquedas inversas con frecuencia, o si el diccionario es muy grande, el rendimiento de su programa se verá afectado. |
Diccionarios y Matrices
Las matrices pueden aparecer como valores en un diccionario. Por ejemplo, si se tiene un diccionario que asigna frecuencias a letras, y se quiere invertir, es decir, tener un diccionario que asigne letras a frecuencias. Dado que pueden haber varias letras con la misma frecuencia, cada valor en el diccionario invertido debería ser una matriz de letras.
Aquí hay una función que invierte un diccionario:
function invertirdic(d)
inverso = Dict()
for clave in keys(d)
val = d[clave]
if val ∉ keys(inverso)
inverso[val] = [clave]
else
push!(inverso[val], clave)
end
end
inverso
endCada vez que se recorre el bucle, se asigna a la variable clave una clave de d, y a val el valor correspondiente. Si val no está en el diccionario inverso, significa que no se ha visto este valor antes, por lo que se crea un nuevo item y se inicializa con un singleton (una matriz que contiene un solo elemento). De lo contrario, se ha visto este valor antes, por lo que se agrega la clave correspondiente a la matriz.
Aquí hay un ejemplo:
julia> hist = histograma("perros");
julia> inverso = invertirdic(hist)
Dict{Any,Any} with 2 entries:
2 => ['r']
1 => ['s', 'e', 'p', 'o']Figura 16 es un diagrama de estado que muestra hist e inverso. Un diccionario se representa como un cuadro con los pares clave-valor dentro. En este libro, si los valores son enteros, números de punto flotante o cadenas de texto, se dibujan dentro del cuadro, y las matrices (generalmente) se dibujan fuera del cuadro, solo para mantener el diagrama simple.
|
Nota
|
Anteriormente se mencionó que un diccionario se implementa usando una tabla hash (también llamada matriz asociativa, hashing, mapa hash, tabla de dispersión o tabla fragmentada), lo cual significa que las claves deben ser hashable. Un hash es una función que toma un valor (de cualquier tipo) y devuelve un entero. Los diccionarios usan estos enteros, llamados valores hash, para almacenar y buscar pares clave-valor. |
Pistas
Si estuvo jugando con la función fibonacci de Sección 6.7, es posible que haya notado que cuanto más grande el argumento que le da, más tiempo tarda la función en ejecutarse. Más aún, el tiempo de ejecución aumenta muy rápidamente.
Para entender por qué, considere Figura 17, que muestra el gráfico de llamadas para la función fibonacci con n = 4:
Un gráfico de llamadas muestra un conjunto de cuadros de funciones, con líneas que conectan cada cuadro con los cuadros de las funciones a las que llama. En la parte superior del gráfico, fibonacci con n = 4 llama a fibonacci con n = 3 y n = 2. A su vez, fibonacci con n = 3 llama a fibonacci con n = 2 y n = 1. Y así sucesivamente.
Cuente cuántas veces se llama a fibonacci(0) y fibonacci(1). Esta es una solución ineficiente al problema y empeora a medida que el argumento aumenta en tamaño.
Una solución es llevar un registro de los valores que ya se han calculado almacenándolos en un diccionario. Un valor que ya ha sido calculado y almacenado para un uso posterior se le denomina pista. Aquí hay una implementación de fibonacci con pistas:
anteriores = Dict(0=>0, 1=>1)
function fibonacci(n)
if n ∈ keys(anteriores)
return anteriores[n]
end
res = fibonacci(n-1) + fibonacci(n-2)
anteriores[n] = res
res
endEl diccionario llamado anteriores mantiene un registro de los valores de Fibonacci que ya conocemos. El programa comienza con dos pares: 0 corresponde a 1 y 1 corresponde a 1.
Siempre que se llama a fibonacci, se comprueba si el diccionario contiene el resultado ya calculado. Si está ahí, la función puede devolver el valor inmediatamente. Si no, tiene que calcular el nuevo valor, añadirlo al diccionario y devolverlo.
Si ejecuta esta versión de fibonacci y la compara con la original, se dará cuenta que es mucho más rápida.
Variables Globales
En el ejemplo anterior, el diccionario anteriores se crea fuera de la función, por lo que pertenece al marco especial llamado Main. Las variables en Main a veces son llamadas globales porque se puede acceder a ellas desde cualquier función. A diferencia de las variables locales, que desaparecen cuando finaliza su función, las variables globales existen de una llamada de función a la siguiente.
Es común usar variables globales como flags o banderas; es decir, variables booleanas que indican si una condición es verdadera. Por ejemplo, algunos programas usan una bandera llamada verbosa para controlar el nivel de detalle en la salida:
verbose = true
function ejemplo1()
if verbosa
println("Ejecutando ejemplo1")
end
endSi intenta reasignar una variable global, se sorprenderá. El siguiente ejemplo trata de llevar registro sobre si se ha llamado o no a una función:
ha_sido_llamada = false
function ejemplo2()
ha_sido_llamada = true # MALO
endPero si lo ejecuta, verá que el valor de ha_sido_llamada no cambia. El problema es que ejemplo2 + crea una nueva variable local llamada +ha_sido_llamada. La variable local desaparece cuando finaliza la función y no tiene efecto en la variable global.
Para reasignar una variable global dentro de una función, debe declarar la variable global antes de usarla: (reasignación
been_called = false
function ejemplo2()
global ha_sido_llamada
ha_sido_llamada = true
endLa sentencia global le dice al intérprete algo como esto: “En esta función, cuando digo ha_sido_llamada, me refiero a la variable global; así que no crees una variable local".
A continuación se muestra un ejemplo que intenta actualizar una variable global:
conteo = 0
function ejemplo3()
conteo = conteo + 1 # MALO
endSi lo ejecuta obtiene:
julia> ejemplo3()
ERROR: UndefVarError: conteo not definedJulia asume que conteo es local, y bajo esa suposición lo está leyendo antes de escribirlo. La solución, nuevamente, es declarar conteo como global.
conteo = 0
function ejemplo3()
global conteo
conteo += 1
endSi una variable global se refiere a un valor mutable, puede modificar el valor sin declarar la variable global:
anteriores = Dict(0=>0, 1=>1)
function ejemplo4()
anteriores[2] = 1
endPor lo tanto, puede agregar, eliminar y reemplazar elementos de una matriz global o diccionario, pero si desea reasignar la variable, debe declararla global:
anteriores = Dict(0=>0, 1=>1)
function ejemplo5()
global anteriores
anteriores = Dict()
endPara mejorar el rendimiento, puede declarar la variable global como constante. Con esto, ya no se puede reasignar la variable, pero si se refiere a un valor mutable, sí se puede modificar el valor.
const known = Dict(0=>0, 1=>1)
function example4()
known[2] = 1
end|
Aviso
|
Las variables globales pueden ser útiles, pero si tiene muchas de ellas y las modifica con frecuencia, pueden dificultar la depuración y empeorar el desempeño de los programas. |
Depuración
A medida que trabaja con conjuntos de datos más grandes, la depuración mediante la impresión y verificación de la salida de manera manual puede tornarse difícil. Aquí hay algunas sugerencias para depurar grandes conjuntos de datos:
-
Reduzca la entrada:
Si es posible, reduzca el tamaño del conjunto de datos. Por ejemplo, si el programa lee un archivo de texto, comience con solo las primeras 10 líneas, o con el ejemplo más pequeño que pueda encontrar que produzca errores. No debe editar los archivos, sino modificar el programa para que solo lea las primeras \(n\) líneas.
Si hay un error, puede reducir \(n\) al valor más pequeño que manifieste el error y luego aumentarlo gradualmente a medida que encuentre y corrija errores.
-
Revisar resúmenes y tipos
En lugar de imprimir y verificar todo el conjunto de datos, considere imprimir resúmenes de los datos. Por ejemplo, el número de elementos en un diccionario o el total de una serie de números.
Una causa común de los errores de tiempo de ejecución son los valores de tipo incorrecto. Para depurar este tipo de error, generalmente es suficiente imprimir el tipo de un valor.
-
Escribir autocomprobaciones:
Puede escribir código que verifique errores automáticamente. Por ejemplo, si está calculando el promedio de una matriz de números, puede verificar que el resultado no sea mayor que el elemento más grande de la matriz o menor que el más pequeño. Esto se llama "prueba de cordura".
Otro tipo de verificación compara los resultados de dos cálculos diferentes para ver si son consistentes. Esta se llama "prueba de consistencia".
-
Formatear la salida:
Formatear la salida de depuración puede hacer que sea más fácil detectar un error. Vimos un ejemplo en Sección 6.9.
Nuevamente, el tiempo que dedica a construir andamiaje puede reducir el tiempo que dedica a la depuración
Glosario
- mapeo
-
Una relación en la que cada elemento de un conjunto corresponde a un elemento de otro conjunto.
- diccionario
-
Una asignación de claves a sus valores correspondientes.
- par clave-valor
-
La representación de la asociación entre una clave y un valor.
- item
-
En un diccionario, otro nombre para un par clave-valor.
- clave
-
Un objeto que aparece en un diccionario como la primera parte de un par clave-valor.
- valor
-
Un objeto que aparece en un diccionario como la segunda parte de un par clave-valor. Este término es más específico que nuestro uso previo de la palabra "valor".
- implementación
-
Una forma de realizar un cálculo.
- tabla hash
-
El algoritmo utilizado para implementar los diccionarios de Julia.
- función hash
-
Una función utilizada por una tabla hash para calcular la ubicación de una clave.
- hashable
-
Un tipo que tiene una función hash.
- búsqueda
-
Una operación sobre un diccionario que toma una clave y encuentra el valor correspondiente.
- búsqueda inversa
-
Una operación sobre un diccionario que toma un valor y encuentra una o más claves que se asignan a él.
- singleton
-
Una matriz (u otra secuencia) con un solo elemento.
- gráfico de llamada
-
Un diagrama que muestra cada cuadro creado durante la ejecución de un programa, con una flecha entre cada función y sus respectivas funciones llamadas.
- pista
-
Valor precalculado y almacenado temporalmente para evitar cálculos redundantes.
- variable global
-
Una variable definida fuera de una función. Se puede acceder a las variables globales desde cualquier función.
- sentencia global
-
Una sentencia que declara un nombre de variable global.
- bandera
-
Una variable booleana utilizada para indicar si una condición es verdadera.
- declaración
-
Una sentencia como
globalque le dice al intérprete algo sobre una variable. - variable global constante
-
Una variable global que no se puede reasignar.
Ejercicios
Ejercicio 11-2
Escriba una función que lea las palabras en palabras.txt y las almacene como claves en un diccionario. No importa cuáles sean los valores. Luego puede usar el operador ∈ como una forma rápida de verificar si una cadena está en el diccionario.
Si hizo Sección 10.15.10, puede comparar la velocidad de esta implementación con el operador array ∈ y la búsqueda binaria.
Ejercicio 11-3
Lea la documentación de la función que opera sobre diccionarios get! y úsela para escribir una versión más concisa de invertirdic.
Ejercicio 11-4
Use pistas en la función de Ackermann de Sección 6.11.2 y vea si esto permite evaluar la función con argumentos de mayor tamaño.
Ejercicio 11-5
Si hizo Sección 10.15.7, ya tiene una función llamada repetido que toma una matriz como parámetro y devuelve true si hay algún objeto que aparece más de una vez en la matriz.
Use un diccionario para escribir una versión más rápida y simple de repetido.
Ejercicio 11-6
Dos palabras son "pares desplazados" si puede desplazar una de ellas y obtener la otra (vea desplazarpalabra en Sección 8.15.5).
Escriba un programa que lea una matriz de palabras y encuentre todos los pares desplazados.
Ejercicio 11-7
Aquí hay otro Puzzle de Car Talk (https://www.cartalk.com/puzzler/browse):
This was sent in by a fellow named Dan O’Leary. He came upon a common one-syllable, five-letter word recently that has the following unique property. When you remove the first letter, the remaining letters form a homophone of the original word, that is a word that sounds exactly the same. Replace the first letter, that is, put it back and remove the second letter and the result is yet another homophone of the original word. And the question is, what’s the word?
Now I’m going to give you an example that doesn’t work. Let’s look at the five-letter word, ‘wrack.’ W-R-A-C-K, you know like to ‘wrack with pain.’ If I remove the first letter, I am left with a four-letter word, ’R-A-C-K.’ As in, ‘Holy cow, did you see the rack on that buck! It must have been a nine-pointer!’ It’s a perfect homophone. If you put the ‘w’ back, and remove the ‘r,’ instead, you’re left with the word, ‘wack,’ which is a real word, it’s just not a homophone of the other two words.
But there is, however, at least one word that Dan and we know of, which will yield two homophones if you remove either of the first two letters to make two, new four-letter words. The question is, what’s the word?
You can use the dictionary from Sección 11.10.1 to check whether a string is in the word array.
|
Observación
|
To check whether two words are homophones, you can use the CMU Pronouncing Dictionary. You can download it from http://www.speech.cs.cmu.edu/cgi-bin/cmudict. |
Write a program that lists all the words that solve the Puzzler.
12. Tuplas
Este capítulo presenta otro tipo integrado: las tuplas. Luego, muestra cómo los arreglos, los diccionarios y las tuplas funcionan en conjunto. También se presenta una característica útil para los arreglos de longitud variable como argumento: los operadores de recopilación y dispersión.
Las Tuplas son Immutables
Una tupla es una secuencia de valores. Estos valores pueden ser de cualquier tipo y están indexados por enteros, por lo que las tuplas son muy parecidas a los arreglos. La diferencia más importante es que las tuplas son inmutables y que cada elemento puede tener su propio tipo.
Una tupla es una lista de valores separados por comas:
julia> t = 'a', 'b', 'c', 'd', 'e'
('a', 'b', 'c', 'd', 'e')Aunque no es necesario, es común encerrar las tuplas entre paréntesis:
julia> t = ('a', 'b', 'c', 'd', 'e')
('a', 'b', 'c', 'd', 'e')Para crear una tupla con un solo elemento, se debe incluir una coma final:
julia> t1 = ('a',)
('a',)
julia> typeof(t1)
Tuple{Char}|
Aviso
|
Un valor entre paréntesis sin coma no es una tupla: |
Otra forma de crear una tupla es la función de tupla integrada en Julia. Sin argumento, esta función crea una tupla vacía:
julia> tuple()
()Si se tienen múltiples argumentos, el resultado es una tupla con los argumentos dados:
julia> t3 = tuple(1, 'a', pi)
(1, 'a', π)Ya que tuple es el nombre de una función integrada, debe evitar usarla como nombre de variable.
La mayoría de los operadores de arreglos también sirven en las tuplas. El operador corchete indexa un elemento:
julia> t = ('a', 'b', 'c', 'd', 'e');
julia> t[1]
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)Y el operador porción selecciona un rango de elementos:
julia> t[2:4]
('b', 'c', 'd')Pero si se intenta modificar uno de los elementos de la tupla, se obtendrá un error:
julia> t[1] = 'A'
ERROR: MethodError: no method matching setindex!(::NTuple{5,Char}, ::Char, ::Int64)Como las tuplas son inmutables, sus elementos no se pueden modificar.
Los operadores relacionales funcionan con las tuplas y otras secuencias, Julia comienza comparando el primer elemento de cada secuencia. Si son iguales, pasa a los siguientes elementos, y así sucesivamente, hasta que encuentra elementos que difieren. Los elementos posteriores no se consideran (incluso si son realmente grandes).
julia> (0, 1, 2) < (0, 3, 4)
true
julia> (0, 1, 2000000) < (0, 3, 4)
trueAsignación de tupla
De vez en cuando, es útil intercambiar los valores de dos variables. Para hacerlo con sentencias de asignación convencionales se debe usar una variable temporal. Por ejemplo, para intercambiar a y b:
temp = a
a = b
b = tempEsta solución resulta aparatosa. La asignación de tuplas soluciona este problema elegantemente:
a, b = b, aEl lado izquierdo es una tupla de variables y el lado derecho es una tupla de expresiones. Cada valor se asigna a su respectiva variable. Todas las expresiones del lado derecho se evalúan antes de las asignaciones.
El número de variables de la izquierda tiene que ser menor o igual que el número de valores a la derecha:
julia> (a, b) = (1, 2, 3)
(1, 2, 3)
julia> a, b, c = 1, 2
ERROR: BoundsError: attempt to access (1, 2)
at index [3]El lado derecho puede ser cualquier tipo de secuencia (cadena, arreglo o tupla). Por ejemplo, para dividir una dirección de correo electrónico en nombre de usuario y dominio, se puede escribir:
julia> addr = "julio.cesar@roma"
"julio.cesar@roma"
julia> unombre, dominio = split(addr, '@');El valor de retorno de split es un arreglo con dos elementos: el primer elemento se asigna a unombre, y el segundo a dominio.
julia> unombre
"julio.cesar"
julia> dominio
"roma"Tuplas como valor de retorno
Estrictamente hablando, una función solo puede devolver un valor pero si el valor es una tupla, el efecto es el mismo que devolver múltiples valores. Por ejemplo, si desea dividir dos enteros y calcular el cociente y el resto, es ineficiente calcular x ÷ y y luego x % y. Es mejor calcular ambos al mismo tiempo.
La función integrada divrem toma dos argumentos y devuelve una tupla de dos valores: el cociente y el resto. El resultado puede ser almacenado como una tupla:
julia> t = divrem(7, 3)
(2, 1)También se puede utilizar asignación de tuplas para almacenar los elementos por separado:
julia> q, r = divrem(7, 3);
julia> @show q r;
q = 2
r = 1Aquí hay un ejemplo de una función que devuelve una tupla:
function minmax(t)
minimum(t), maximum(t)
endmaximum y minimum son funciones integradas que encuentran los elementos más grandes y más pequeños de una secuencia, respectivamente. La función minmax calcula ambos y devuelve una tupla de dos valores. Otra alternativa es utilizar la función integrada extrema, lo cual es más eficiente.
Tupla con Argumentos de Longitud Variable
Las funciones pueden tomar un número variable de argumentos. Un nombre de parámetro que termina con ... recopila argumentos en una tupla. Por ejemplo, imprimirtodo toma cualquier número de argumentos y los imprime:
function imprimirtodo(args...)
println(args)
endEl parámetro de recopilación puede tener cualquier nombre, pero la convención es llamarlo args. A continuación se muestra cómo funciona la función:
julia> imprimirtodo(1, 2.0, '3')
(1, 2.0, '3')El opuesto de la recopilación es la dispersión. Si tiene una secuencia de valores y desea pasarla a una función como argumento múltiple, puede usar el operador ... . Por ejemplo, divrem toma exactamente dos argumentos y no funciona con tuplas:
julia> t = (7, 3);
julia> divrem(t)
ERROR: MethodError: no method matching divrem(::Tuple{Int64,Int64})No obstante, si "dispersamos" la tupla, funciona:
julia> divrem(t...)
(2, 1)Muchas de las funciones integradas usan tuplas con argumentos de longitud variable. Por ejemplo, max y min pueden tomar cualquier número de argumentos:
julia> max(1, 2, 3)
3Pero sum no:
julia> sum(1, 2, 3)
ERROR: MethodError: no method matching sum(::Int64, ::Int64, ::Int64)Ejercicio 12-1
Escriba una función llamada sumartodo que tome cualquier número de argumentos y devuelva su suma.
En el mundo de Julia, generalmente se le llama “slurp” ("sorber" en español) a reunir y "splat" ("plaf" en español, como el ruido cuando cae algo) a dispersar.
Arreglos y tuplas
zip es una función integrada que toma dos o más secuencias y devuelve una colección de tuplas donde cada tupla contiene un elemento de cada secuencia. El nombre de la función se refiere a una cremallera, que une e intercala dos filas de dientes.
Este ejemplo une e intercala una cadena y un arreglo:
julia> s = "abc";
julia> t = [1, 2, 3];
julia> zip(s, t)
zip("abc", [1, 2, 3])El resultado es un objeto zip que permite iterar a través de los pares. El uso más común de zip es en un bucle for:
julia> for par in zip(s, t)
println(par)
end
('a', 1)
('b', 2)
('c', 3)Un objeto zip es un tipo de iterador, que es cualquier objeto que itera a través de una secuencia. Los iteradores son, en cierto modo, similares a los arreglos, pero a diferencia de estos últimos, no se puede usar un índice para seleccionar un elemento de un iterador.
Si desea usar operadores y funciones de arreglos, puede usar un objeto zip para hacer un arreglo:
julia> collect(zip(s, t))
3-element Array{Tuple{Char,Int64},1}:
('a', 1)
('b', 2)
('c', 3)El resultado es una serie de tuplas. En este ejemplo, cada tupla contiene un carácter de la cadena y el elemento correspondiente del arreglo.
Si las secuencias no tienen la misma longitud, el resultado tiene la longitud de la más corta.
julia> collect(zip("Juan", "Gabriel"))
4-element Array{Tuple{Char,Char},1}:
('J', 'G')
('u', 'a')
('a', 'b')
('n', 'r')Se puede usar asignación de tuplas en un bucle for para recorrer un arreglo de tuplas:
julia> t = [('a', 1), ('b', 2), ('c', 3)];
julia> for (letra, numero) in t
println(numero, " ", letra)
end
1 a
2 b
3 cEn cada iteración del ciclo, Julia selecciona la siguiente tupla en el arreglo y asigna estos elementos a letra y número. Los paréntesis de (letra, número) son obligatorios.
Combinando zip, for y asignación de tuplas, se obtiene una forma para recorrer dos (o más) secuencias al mismo tiempo. Por ejemplo, la función coinciden toma dos secuencias, t1 y t2, y devuelve true si hay un índice i tal que t1[i] == t2[i]:
function coinciden(t1, t2)
for (x, y) in zip(t1, t2)
if x == y
return true
end
end
false
endSi se necesita recorrer los elementos de una secuencia y sus índices, se puede usar la función integrada enumerate:
julia> for (indice, elemento) in enumerate("abc")
println(indice, " ", elemento)
end
1 a
2 b
3 cEl resultado de enumerate es un objeto enumerate, el cual hace una iteración sobre una secuencia de pares, dónde cada par contiene un índice (a partir de 1) y un elemento de la secuencia dada.
Diccionarios y Tuplas
Los diccionarios se pueden usar como iteradores que iteran sobre los pares clave-valor. Puede usarlos en un bucle for como este:
julia> d = Dict('a'=>1, 'b'=>2, 'c'=>3);
julia> for (key, value) in d
println(key, " ", value)
end
a 1
c 3
b 2Como es de esperar, en un diccionario los elementos no están en un orden particular.
Ahora, si se quiere hacer lo contrario, se puede usar una serie de tuplas para inicializar un nuevo diccionario:
julia> t = [('a', 1), ('c', 3), ('b', 2)];
julia> d = Dict(t)
Dict{Char,Int64} with 3 entries:
'a' => 1
'c' => 3
'b' => 2Al combinar Dict con zip, podemos crear un diccionario de una manera muy simple:
julia> d = Dict(zip("abc", 1:3))
Dict{Char,Int64} with 3 entries:
'a' => 1
'c' => 3
'b' => 2Es común usar tuplas como claves en los diccionarios. Por ejemplo, un directorio telefónico puede asignar números de teléfono a una tupla con apellido y nombre. Suponiendo que se ha definido apellido, nombre y numero, podríamos escribir:
directorio[apellido, nombre] = numeroLa expresión entre paréntesis es una tupla. Se podría usar asignación de tuplas para recorrer este diccionario.
for ((apellido, nombre), numero) in directorio
println(nombre, " ", apellido, " ", numero)
endEste bucle recorre los pares clave-valor en directorio, los cuales son tuplas. Asigna los elementos de la clave de cada tupla a apellido y nombre y el valor a numero, luego imprime el nombre y el número de teléfono correspondiente.
Hay dos formas de representar tuplas en un diagrama de estado. La versión más detallada muestra los índices y elementos tal como aparecen en un arreglo. Por ejemplo, la tupla ("Cortázar", "Julio") se vería como en Figura 18.
Pero en un diagrama más grande, es posible que desee omitir algunos detalles. Por ejemplo, un diagrama del directorio telefónico puede verse como en Figura 19.
Aquí las tuplas se muestran usando la sintaxis de Julia para tener un esquema más simple. El número de teléfono del diagrama es el número de reclamos de la BBC, así que no intentes llamar.
Secuencias de Secuencias
Hasta ahora, el capítulo se ha centrado en los arreglos de tuplas, pero casi todos los ejemplos que se han visto también funcionan con arreglos de arreglos, tuplas de tuplas y tuplas de arreglos. Para evitar enumerar todas las posibles combinaciones, a veces es más fácil hablar sobre secuencias de secuencias.
En muchos contextos, los diferentes tipos de secuencias (cadenas, arreglos y tuplas) se pueden usar indistintamente. Entonces, ¿cómo elegir uno u otro?
Para comenzar con lo mas obvio, las cadenas son más limitadas que las demás secuencias, porque los elementos deben ser caracteres. Además son inmutables. Si se necesita poder cambiar los caracteres en una cadena (en vez de crear una nueva), puede que lo mas adecuado sea elegir un arreglo de caracteres.
Los arreglos se usan con mas frecuencia que las tuplas, principalmente porque son mutables. No obstante, hay algunos casos donde es posible que sea preferible usar tuplas:
-
En algunos contextos, como en una sentencia return, resulta sintácticamente más simple crear una tupla que un arreglo.
-
Si se pasa una secuencia como argumento de una función, el uso de tuplas reduce los comportamientos potencialmente indeseados debido a la creación de alias.
-
Por rendimiento. El compilador puede especializarse en este tipo.
Dado que las tuplas son inmutables, no tienen funciones como sort! y reverse! que modifiquen arreglos ya existentes. Sin embargo, Julia proporciona las funciones integradas sort, que toma un arreglo y devuelve una secuencia nueva con los mismos elementos ordenados, y reverse, que toma cualquier secuencia y devuelve una secuencia nueva del mismo tipo con los mismos elementos en el orden contrario.
Depuración
Los arreglos, diccionarios y tuplas son ejemplos de estructuras de datos. En este capítulo se empiezan a ver estructuras de datos compuestas, como arreglos o tuplas, y diccionarios que contienen tuplas como claves y arreglos como valores. Las estructuras de datos compuestas son útiles, aunque también resultan propensas a lo que se llaman errores de forma, es decir, errores causados cuando una estructura de datos tiene el tipo, tamaño o estructura incorrecta. Por ejemplo, si está esperando una lista con un entero y se le pasa simplemente un entero (no en una lista), no funcionará.
Julia permite añadir el tipo a elementos de una secuencia. Esto se detalla en Capítulo 17. Especificar el tipo elimina muchos errores de forma.
Glosario
- tupla
-
Una secuencia inmutable de elementos donde cada elemento puede tener su propio tipo.
- asignación en tupla
-
Una asignación con una secuencia en el lado derecho y una tupla de variables en el izquierdo. Primero se evalúa el lado derecho y luego sus elementos son asignados a las variables de la izquierda.
- reunir
-
La operación de armar una tupla con argumentos de longitud variable.
- dispersar
-
La operación de tratar una secuencia como una lista de argumentos.
- objeto zip
-
El resultado de llamar a la función integrada
zip; un objeto que itera a través de una secuencia de tuplas. - iterador
-
Un objeto que puede iterar a través de una secuencia pero que no tiene los operadores y funciones de arreglos.
- estructura de datos
-
Una coleccion de valores relacionados, a menudo organizados en arreglos, diccionarios, tuplas, etc.
- error de forma
-
Un error causado porque un valor tiene la forma incorrecta; es decir, el tipo o tamaño incorrecto.
Ejercicios
Ejercicio 12-2
Escriba una función llamada masfrecuente que tome una cadena e imprima las letras en orden decreciente de frecuencia. Encuentre muestras de texto de varios idiomas diferentes y vea cómo la frecuencia de las letras varía entre idiomas. Compare sus resultados con las tablas en https://en.wikipedia.org/wiki/Letter_frequencies.
Ejercicio 12-3
¡Más anagramas!
-
Escriba un programa que lea una lista de palabras de un archivo (vea Sección 9.1) e imprima todos los conjuntos de palabras que son anagramas.
Aquí hay un ejemplo de cómo se vería la salida:
["brazo", "zobra", "broza", "zarbo"] ["palabra", "parlaba"] ["vida", "diva"] ["gato", "toga", "gota"]ObservaciónEs posible que desee crear un diccionario que asigne a una colección de letras una serie de palabras que se puedan deletrear con esas letras. La pregunta es, ¿cómo representar la colección de letras de una manera que pueda usarse como clave?
-
Modifique el programa anterior para que imprima primero el arreglo más largo de anagramas, seguido del segundo más larga, y así sucesivamente.
-
En Scrabble, un "bingo" es cuando juegas las siete fichas de tu atril, junto con una letra del tablero, para formar una palabra de ocho letras. ¿Qué colección de 8 letras forman parte del bingo más probable?
Ejercicio 12-4
Dos palabras metatizan si se puede transformar una en la otra intercambiando dos letras como es el caso de "conversar" y "conservar". Escriba un programa que encuentre todos los pares de metátesis en el diccionario.
|
Observación
|
No pruebe con todos los pares de palabras, ni tampoco con todos los intercambios posibles. |
Créditos: Este ejercicio está inspirado en un ejemplo de http://puzzlers.org.
Ejercicio 12-5
Aquí hay otro Puzzle de Car Talk (https://www.cartalk.com/puzzler/browse):
¿Cuál es la palabra en español más larga, que sigue siendo una palabra en español válida a medida que se eliminan sus letras una a una?
Las letras se pueden eliminar de cualquier extremo o del medio, pero no se puede reordenar ninguna de ellas. Cada vez que elimina una letra, se queda con otra palabra en español. Eventualmente terminará con una letra, la cual también será una palabra en español que puede encontrar en el diccionario. Se desea saber cuál es la palabra más larga y cuántas letras tiene.
A modo de ejemplo, piense en la palabra: Palote. ¿De acuerdo? Comienza con palote, elimina la letra p y queda alote, luego se quita la t y queda aloe, se toma la e y se tiene alo, quitando la o se tiene al, y finalmente, eliminando la l queda a.
Escriba un programa que encuentre todas las palabras que se pueden reducir de esta manera y luego encuentre la más larga.
|
Observación
|
Este ejercicio es un poco más desafiante que el resto, así que aquí hay algunas sugerencias:
|
13. Estudio de Caso: Selección de Estructura de Datos
Hasta ahora hemos aprendido sobre las principales estructuras de datos de Julia y hemos visto algunos de los algoritmos que las utilizan.
Este capítulo presenta un estudio de caso con ejercicios que le permiten practicar la elección de estructuras de datos y su uso.
Análisis de Frecuencia de Palabras
Como de costumbre, se recomienda intentar resolver los ejercicios antes de leer las soluciones.
Ejercicio 13-1
Escriba un programa que lea un archivo, divida cada línea en palabras, elimine el espacio en blanco y la puntuación de las palabras y luego las convierta en minúsculas.
|
Observación
|
La función |
Ejercicio 13-2
Vaya a la página de Proyecto Gutenberg (https://gutenberg.org) y descargue su libro favorito sin derechos de autor en formato de texto plano. La mayoría de los libros están en inglés, pero existen algunos en español.
Modifique su programa del ejercicio anterior para leer el libro que descargó, omita la información del encabezado al comienzo del archivo y procese el resto de las palabras tal como en el ejercicio previo.
Luego, modifique el programa para contar la cantidad total de palabras en el libro y la cantidad de veces que se usa cada palabra.
Imprima la cantidad de palabras diferentes que se usan en el libro. Compare diferentes libros de diferentes autores, escritos en diferentes épocas. ¿Qué autor usa un vocabulario más extenso?
Ejercicio 13-3
Modifique el programa del ejercicio anterior para imprimir las 20 palabras más utilizadas en el libro.
Ejercicio 13-4
Modifique el programa anterior para que lea una lista de palabras y luego imprima todas las palabras del libro que no estén en la lista de palabras. ¿Cuántos de ellos son errores tipográficos? ¿Cuántos de ellos son palabras comunes que deberían estar en la lista de palabras? ¿ Cuántos de ellos son términos realmente macabros?
Números aleatorios
Dadas las mismas entradas, la mayor parte de los programas generan la misma salida cada vez que los ejecutamos, por lo que se dice que son deterministas. Normalmente el determinismo es algo bueno, ya que esperamos que un cálculo nos entregue siempre el mismo resultado. Para algunas aplicaciones, sin embargo, queremos que el computador sea impredecible. Por ejemplo en los juegos, entre otros casos.
Hacer que un programa sea realmente no determinista resulta difícil, pero hay formas de que hacer que al menos parezca no determinista. Una de ellas es usar algoritmos para generar números pseudoaleatorios. Los números pseudoaleatorios no son verdaderamente aleatorios porque se generan mediante un cálculo determinista pero al mirar estos números es casi imposible distinguirlos de lo aleatorio.
La función rand devuelve un numero de punto flotante entre 0.0 y 1.0 (incluyendo 0.0 pero no 1.0). Cada vez que usted llama a rand obtiene el siguiente numero de una larga serie. Para ver un ejemplo, ejecute este bucle:
for i in 1:10
x = rand()
println(x)
endLa función rand puede tomar un iterador o arreglo como argumento y devuelve un elemento aleatorio de ellos:
for i in 1:10
x = rand(1:6)
print(x, " ")
endEjercicio 13-5
Escriba una función llamada escogerdelhistograma que tome un histograma definido como en Sección 11.2 y devuelva un valor aleatorio del histograma, elegido con probabilidad proporcional a la frecuencia. Por ejemplo, para este histograma:
julia> t = ['a', 'a', 'b'];
julia> histograma(t)
Dict{Any,Any} with 2 entries:
'a' => 2
'b' => 1su función debe devolver 'a' con probabilidad \(\frac{2}{3}\) y 'b' con probabilidad \(\frac{1}{3}\).
Histograma de Palabras
Debe hacer los ejercicios anteriores antes de continuar. También necesitará https://github.com/JuliaIntro/IntroAJulia.jl/blob/master/data/DonQuijote.txt.
Aquí hay un programa que lee un archivo y construye un histograma de las palabras en el archivo:
function procesararchivo(nombrearchivo)
hist = Dict()
for linea in eachline(nombrearchivo)
procesarlinea(linea, hist)
end
hist
end;
function procesarlinea(linea, hist)
linea = replace(linea, '-' => ' ')
for palabra in split(linea)
palabra = string(filter(isletter, [palabra...])...)
palabra = lowercase(palabra)
hist[palabra] = get!(hist, palabra, 0) + 1
end
end;Dict{Any,Any} with 23607 entries:
"enojó" => 1
"angosta" => 1
"hurto" => 10
"sirviesen" => 2
"solene" => 1
"coronan" => 1
"enderécese" => 2
"alteza" => 15
"rescatarlos" => 1
"enderezador" => 1
"libertad" => 81
"abundante" => 5
"bajeza" => 4
"embotó" => 1
"estime" => 1
"renovaban" => 1
"acreciente" => 4
"debieron" => 8
"garci" => 1
⋮ => ⋮
hist = procesararchivo("DonQuijote.txt");Este programa lee DonQuijote.txt, que contiene el texto de Don Quijote de Miguel de Cervantes.
procesararchivo recorre las líneas del archivo, pasando una línea a la vez a procesarlinea. El histograma hist se está utilizando como acumulador.
procesarlinea usa la función replace para reemplazar los guiones por espacios antes de usar split para dividir la línea en un arreglo de cadenas. Recorre el conjunto de palabras y usa filter, isletter y lowercase para eliminar los signos de puntuación y convertir las palabras a minúsculas. (Decir que las cadenas se "convierten" es incorrecto, recuerde que las cadenas son inmutables, por lo que una función como lowercase devuelve cadenas nuevas).
Finalmente, procesarlinea actualiza el histograma creando un nuevo elemento o incrementando uno existente.
Para contar el número total de palabras en el archivo, podemos sumar las frecuencias en el histograma:
function palabrastotales(hist)
sum(values(hist))
endEl número de palabras diferentes es el número de elementos en el diccionario:
function palabrasdiferentes(hist)
length(hist)
endPara imprimir los resultados se puede usar el siguiente código:
julia> println("Número total de palabras: ", palabrastotales(hist))
Número total de palabras: 385925
julia> println("Número de palabras diferentes: ", palabrasdiferentes(hist))
Número de palabras diferentes: 23607Observación: No se considera el encabezado del archivo de texto, sólo el libro.
Palabras Más Comunes
Para encontrar las palabras más comunes, podemos hacer un arreglo de tuplas, donde cada tupla contiene una palabra y su frecuencia, y ordenarlas. La siguiente función toma un histograma y devuelve un arreglo de tuplas de frecuencia de palabras:
function mascomun(hist)
t = []
for (clave, valor) in hist
push!(t, (valor,clave))
end
reverse(sort(t))
endEn cada tupla, la frecuencia aparece primero, por lo que el arreglo resultante se ordena por frecuencia. A continuación se muestra un bucle que imprime las 10 palabras más comunes:
t = mascomun(hist)
println("Las palabras más comunes son:")
for (frec, palabra) in t[1:10]
println(palabra, "\t", frec)
endEn este ejemplo utilizamos un carácter de tabulación ('\t') como "separador", en vez de un espacio, por lo que la segunda columna está alineada. A continuación se muestran los resultados de Don Quijote:
Las palabras más comunes son: que 20626 de 18217 y 18188 la 10363 a 9881 en 8241 el 8210 no 6345 los 4748 se 4690
|
Observación
|
Este código se puede simplificar usando como argumento la palabra reservada |
Parametros Opcionales
Se han tratado funciones integradas de Julia que toman argumentos opcionales. También es posible escribir funciones definidas por el programador con argumentos opcionales. Por ejemplo, aquí hay una función que imprime las palabras más comunes en un histograma:
function imprimirmascomun(hist, num=10)
t = mascomun(hist)
println("Las palabras más comunes son: ")
for (frec, palabra) in t[1:num]
println(palabra, "\t", frec)
end
endEl primer parámetro es obligatorio y el segundo es opcional. El valor predeterminado de num es 10.
Si solo pasas un argumento:
imprimirmascomun(hist)num toma el valor predeterminado. Si pasas dos argumentos:
imprimirmascomun(hist, 20)num toma el valor del argumento. En otras palabras, el argumento opcional anula el valor predeterminado.
Si una función tiene parámetros obligatorios y opcionales, los parámetros obligatorios deben ir primero, seguidos de los opcionales.
Resta de Diccionario
Encontrar las palabras de un libro que no están en la lista de palabras de palabras.txt es un problema similar a una resta de conjuntos, es decir, se quiere encontrar todas las palabras de un conjunto (las palabras en el libro) que no están en el otro (las palabras en la lista).
resta toma los diccionarios d1 y d2 y devuelve un nuevo diccionario que contiene todas las claves de d1 que no están en d2. Como realmente no importan los valores, se fijan como nothing.
function resta(d1, d2)
res = Dict()
for clave in keys(d1)
if clave ∉ keys(d2)
res[clave] = nothing
end
end
res
endPara encontrar las palabras en el libro que no están en palabras.txt, se ouede usar procesararchivo para construir un histograma para palabras.txt, y luego la función resta:
palabras = procesararchivo("palabras.txt")
dif = resta(hist, palabras)
println("Palabras en el libro que no están en la lista de palabras:")
for palabra in keys(dif)
print(palabra, " ")
endEstos son algunos de los resultados de Don Quijote:
Palabras en el libro que no están en la lista de palabras:
enojó angosta coronan sirviesen solene enderécese rescatarlos embotó estime renovaban ...Algunas de estas palabras son conjugaciones de verbos. Otros, como "solene", ya no son de uso común. ¡Pero algunas son palabras comunes que deberían estar en la lista!
Ejercicio 13-6
Julia proporciona una estructura de datos llamada Set que permite muchas operaciones comunes de conjuntos. Puede leer sobre ellas en Sección 20.2, o consultar la documentación en https://docs.julialang.org/en/v1/base/collections/#Set-Like-Collections-1.
Escriba un programa que use la resta de conjuntos para encontrar palabras en el libro que no están en la lista de palabras.
Palabras al Azar
Para elegir una palabra aleatoria del histograma, el algoritmo más simple es construir un arreglo con múltiples copias de cada palabra, de acuerdo con la frecuencia observada, y luego elegir una palabra del arreglo:
function palabraalazar(h)
t = []
for (palabra, frec) in h
for i in 1:frec
push!(t, palabra)
end
end
rand(t)
endEste algoritmo funciona pero no es muy eficiente ya que cada vez que elige una palabra aleatoria, reconstruye el arreglo, que es tan grande como el libro original. Una mejora es construir el arreglo una vez y luego hacer múltiples selecciones, pero el arreglo sigue siendo grande.
Una alternativa es:
-
Use las
clavespara obtener un arreglo de palabras del libro. -
Cree un arreglo que contenga la suma acumulada de las frecuencias de palabras (vea Sección 10.15.2). El último elemento en este arreglo es el número total de palabras en el libro, \(n\).
-
Elija un número aleatorio del 1 al \(n\). Use búsqueda binaria (vea Sección 10.15.10) para encontrar el índice donde se insertará el número aleatorio en la suma acumulada.
-
Use el índice para encontrar la palabra correspondiente en el arreglo de palabras.
Ejercicio 13-7
Escriba un programa que use este algoritmo para elegir una palabra aleatoria del libro.
Análisis de Markov
Si elige palabras del libro al azar, puede tener una idea del vocabulario usado, pero probablemente no se va a obtener una oración:
rocinante pláticas sazón ojos Dulcinea DiosUna serie de palabras aleatorias rara vez tiene sentido porque no hay relación entre palabras sucesivas. Por ejemplo, en una oración real, se esperaría que un artículo como "el" fuese seguido por un sustantivo y probablemente no un verbo o un adverbio.
Una forma de medir este tipo de relaciones es con el análisis de Markov, que define para una secuencia dada de palabras la probabilidad de las palabras que podrían venir después. Por ejemplo, en la canción La vida es un carnaval (de Celiz Cruz):
Todo aquel Que piense que la vida siempre es cruel Tiene que saber que no es así Que tan solo hay momentos malos Y todo pasa Todo aquel Que piense que esto nunca va cambiar Tiene que saber que no es así Que al mal tiempo, buena cara Y todo cambia Ay, no hay que llorar (No hay que llorar) Que la vida es un carnaval Que es más bello vivir cantando
En este texto, la frase "que piense" siempre va seguida de la palabra "que", pero la frase "piense que" puede ir seguida de "la" o "esto".
El resultado del análisis de Markov es un mapeo de cada prefijo (como "que piense" y "piense que") a todos los sufijos posibles (como "la" y "esto").
Dada esta asignación, se puede generar un texto aleatorio comenzando con cualquier prefijo y eligiendo aleatoriamente entre los posibles sufijos. A continuación, puede combinar el final del prefijo y el nuevo sufijo para formar el siguiente prefijo y repetir.
Por ejemplo, si comienza con el prefijo "Que la", la siguiente palabra será "vida", porque el prefijo solo aparece dos veces en el texto y siempre está seguido de este sufijo. El siguiente prefijo es "la vida", por lo que el siguiente sufijo podría ser "siempre" o "es".
En este ejemplo, la longitud del prefijo siempre es dos, pero puede hacer análisis de Markov con un prefijo de cualquier longitud.
Ejercicio 13-8
Análisis de Markov:
-
Escriba un programa que lea un texto desde un archivo y realice un análisis de Markov. El resultado debe ser un diccionario que asocie prefijos y una colección de posibles sufijos. La colección puede ser un arreglo, tupla o diccionario, depende de usted hacer una elección adecuada. Puede probar su programa con una longitud de prefijo de dos pero debe escribir el programa de manera tal que sea fácil probar con otras longitudes.
-
Agregue una función al programa anterior para generar un texto aleatorio basado en análisis de Markov. Aquí hay un ejemplo de Don Quijote con longitud de prefijo 2:
"Trifaldi, había de Troya, ni por la majestad real. Y con mis quejas. Desechásteme ¡oh estremo su frío del agravio a la espada, teniéndola por aca y más que sólo se trueca y con el cual encendía el ejemplo de aquellos cazadores"
Para este ejemplo, se dejó la puntuación anexa a las palabras. El resultado es casi sintácticamente correcto. Semánticamente, casi tiene sentido, pero no del todo.
¿Qué sucede si aumenta la longitud del prefijo? ¿El texto aleatorio tiene más sentido?
-
Una vez que su programa esté funcionando, podría probar combinando texto de dos o más libros. El texto aleatorio que genere combinará el vocabulario y las frases de las fuentes de maneras interesantes.
Crédito: Este estudio de caso se basa en un ejemplo de Kernighan y Pike, The Practice of Programming, Addison-Wesley, 1999.
|
Observación
|
Debe hacer este ejercicio antes de continuar. |
Estructuras de Datos
Usar análisis de Markov para generar texto aleatorio es divertido, pero además, este ejercicio tiene un trasfondo: la selección de la estructura de datos. En los los ejercicios anteriores, tenía que elegir:
-
Cómo representar los prefijos.
-
Cómo representar la colección de los posibles sufijos.
-
Cómo representar la asociación de cada prefijo con la colección de posibles sufijos.
El último es fácil: un diccionario es la opción obvia para una asociación entre claves y valores correspondientes.
Para los prefijos, las opciones más obvias son cadena, arreglo de cadenas o tupla de cadenas.
Para los sufijos, puede ser un arreglo o un histograma (diccionario).
¿Cómo se elige? El primer paso es pensar en las operaciones que deberá implementar para cada estructura de datos. Para los prefijos, se debe ser capaz de eliminar palabras del principio y agregarlas al final. Por ejemplo, si el prefijo actual es "que piense" y la siguiente palabra es "que", debe poder formar el siguiente prefijo, "piense que".
Para los prefijos, podría elegir un arreglo, ya que en él es fácil agregar y eliminar elementos.
Para la colección de sufijos, las operaciones que se deben realizar incluyen agregar un nuevo sufijo (o aumentar la frecuencia de uno existente) y elegir un sufijo aleatorio.
Agregar un nuevo sufijo es igualmente fácil para la implementación del arreglo o del histograma. Elegir un elemento aleatorio de un arreglo es fácil pero elegir eficientemente de un histograma es más difícil (ver Sección 13.7.1).
Hasta ahora se ha hablado principalmente sobre la facilidad de implementación, pero hay otros factores a considerar al elegir las estructuras de datos. Uno es el tiempo de ejecución. A veces hay una razón teórica para esperar que una estructura de datos sea más rápida que otra. Por ejemplo, anteriormente se mencionó que el operador in es más rápido para los diccionarios que para los arreglos, al menos cuando el número de elementos es grande.
Aunque generalmente no se sabe de antemano qué implementación será más rápida, una opción es implementar ambos y ver cuál es mejor. Este enfoque se llama benchmarking. Una alternativa práctica es elegir la estructura de datos que sea más fácil de implementar y luego ver si es lo suficientemente rápida para la aplicación prevista. Si es así, no hay necesidad de continuar. Si no, hay herramientas, como el módulo Profile, que pueden identificar los lugares en un programa que toman más tiempo.
El otro factor a considerar es el espacio de almacenamiento. Por ejemplo, usar un histograma para la colección de sufijos puede tomar menos espacio porque solo tiene que almacenar cada palabra una vez, sin importar cuántas veces aparezca en el texto. En algunos casos, ahorrar espacio también puede hacer que su programa se ejecute más rápido. En el peor de los casos, su programa podría no ejecutarse si se queda sin memoria pero para muchas aplicaciones el espacio es una consideración secundaria después del tiempo de ejecución.
Una última reflexión: en esta discusión, se ha dado a entender que se debería usar una estructura de datos para el análisis y la generación. Pero dado que estas son fases separadas, también sería posible usar una estructura para el análisis y luego convertirla en otra estructura para la generación. Esto sería conveniente si el tiempo ahorrado durante la generación excede el tiempo dedicado a la conversión.
|
Observación
|
El paquete de Julia |
Depuración
Cuando está depurando un programa, y especialmente si está tratando de resolver un error difícil, hay cinco cosas que puede probar:
- Lee
-
Examine su código, léalo y verifique que dice lo que quería decir.
- Ejecuta
-
Experimente haciendo cambios y ejecutando diferentes versiones. A menudo, si muestra lo correcto en el lugar correcto del programa, el problema se vuelve obvio, pero para ello a veces tiene que desarrollar andamiaje.
- Reflexiona
-
¡Tómese un tiempo para pensar! ¿Qué tipo de error es: de sintaxis, tiempo de ejecución o semántica? ¿Qué información puede obtener de los mensajes de error o de la salida del programa? ¿Qué tipo de error podría causar el problema que estás viendo? ¿Qué cambió antes de que apareciera el problema?
- Habla
-
Si le explica el problema a otra persona, a veces puede encontrar la respuesta incluso antes de terminar de hacer la pregunta. Generalmente no es necesaria otra persona, incluso se podría hablar con un pato de goma. Este es el origen de la conocida estrategia llamada depuración del pato de goma. Esto es real, vea https://en.wikipedia.org/wiki/Rubber_duck_debugging.
- Vuelve atrás
-
En ocasiones, lo mejor que puede hacer es retroceder, deshacer los cambios recientes hasta regresar a un programa que funcione y que comprenda. Una vez logrado esto, puede comenzar a reconstruir.
Los programadores principiantes a veces se atascan en una de estas actividades y olvidan las otras. Cada actividad viene con su propia forma de fallar.
Por ejemplo, leer su código podría ayudar si el problema es un error tipográfico, pero no si el problema es un malentendido conceptual. Si no comprende lo que hace su programa, puede leerlo 100 veces y nunca ver el error, porque el error está en su cabeza.
Ejecutar experimentos puede ayudar, especialmente si ejecuta pruebas pequeñas y simples, pero si ejecuta experimentos sin pensar o leer su código, puede caer en un patrón llamado "programación de caminata aleatoria", que es el proceso de hacer cambios aleatorios hasta que el programa haga lo correcto. No hace falta decir que la programación de caminata aleatoria puede llevar mucho tiempo.
La persona que programa tiene que tomarse su tiempo para pensar. La depuración es como una ciencia experimental. Debe tener al menos una hipótesis sobre la causa del problema. Si hay dos o más opciones, trate de pensar en una prueba que elimine una de ellas.
Incluso las mejores técnicas de depuración fallarán si hay demasiados errores, o si el código que está tratando de corregir es demasiado grande y complicado. A veces, la mejor opción es volver atrás, simplificando el programa hasta que llegue a algo que funcione y que comprenda.
Los programadores principiantes a menudo son reacios a volver atrás porque no pueden soportar eliminar una línea de código (incluso si es incorrecto). Si le hace sentir mejor, copie su programa en otro archivo antes de comenzar a eliminarlo. Luego puede copiar las piezas una por una.
Encontrar un error difícil requiere leer, ejecutar, reflexionar y, a veces, volver atrás. Si se queda atascado en una de estas actividades, pruebe las otras.
Glosario
- determinístico
-
Perteneciente a un programa que hace lo mismo cada vez que se ejecuta, a partir de las mismas entradas.
- pseudoaleatorio
-
Perteneciente a una secuencia de números que parecen ser aleatorios, pero que son generados por un programa determinista.
- valor por defecto (o valor por omisión)
-
El valor dado a un parámetro opcional si no se proporciona un argumento.
- anular
-
Reemplazar un valor por defecto con un argumento.
- benchmarking
-
El proceso de elegir entre estructuras de datos implementando alternativas y probándolas con una muestra de las posibles entradas.
- depuración del pato de goma
-
Depuración en dónde se explica el problema a un objeto inanimado, tal como un pato de goma. Articular el problema puede ayudarle a resolverlo, incluso si el pato de goma no sabe de Julia.
Ejercicios
Ejercicio 13-9
El "rango" de una palabra es su posición en un arreglo de palabras ordenadas por frecuencia: la palabra más común tiene rango 1, la segunda más común tiene rango 2, etc.
La ley de Zipf describe una relación entre los rangos y las frecuencias de las palabras en idiomas naturales (https://en.wikipedia.org/wiki/Zipf's_law). Específicamente, predice que la frecuencia, \(f\), de la palabra con rango \(r\) es:
donde \(s\) y \(c\) son parámetros que dependen del idioma y el texto. Si aplicas logaritmo a ambos lados de esta ecuación, obtienes:
Entonces, si se grafica \(\log f\) versus \(\log r\), se debería obtener una línea recta con pendiente \(-s\) e intercepto \(\log c\).
Escriba un programa que lea un texto de un archivo, cuente las frecuencias de las palabras e imprima una línea para cada palabra, en orden descendente de frecuencia, con \(\log f\) y \(\log r\).
Instale una librería para graficar:
(v1.0) pkg> add PlotsSu uso es muy sencillo:
using Plots
x = 1:10
y = x.^2
plot(x, y)Use la librería Plots para graficar los resultados y verificar si forman una línea recta.
14. Archivos
Este capítulo presenta el concepto de persistencia, que alude a los programas que mantienen los datos en almacenamiento permanente, y muestra cómo usar diferentes tipos de almacenamiento permanente, tales como archivos y bases de datos.
Persistencia
La mayoría de los programas que hemos visto hasta ahora han sido transitorios, es decir, se ejecutan por un tiempo corto y generan una salida pero cuando finalizan, sus datos desaparecen. Si ejecuta el programa nuevamente, este comienza de cero.
Otros programas, en cambio, son persistentes, se ejecutan durante un largo período de tiempo (o todo el tiempo), mantienen al menos parte de sus datos en almacenamiento permanente (en un disco duro, por ejemplo) y si se apagan y vuelven a comenzar, retoman donde lo dejaron.
Ejemplos de programas persistentes son los sistemas operativos, que se ejecutan siempre que una computadora esté encendida, y los servidores web, que se ejecutan todo el tiempo esperando a que lleguen solicitudes a la red.
Una de las formas más simples para que los programas mantengan sus datos es leyendo y escribiendo archivos de texto. Ya se han visto programas que leen archivos de texto y en este capítulo se van a ver programas que los escriben.
Otra alternativa es almacenar el estado del programa en una base de datos. En este capítulo también se presentará cómo usar una base de datos simple.
Lectura y Escritura
Un archivo de texto es una secuencia de caracteres almacenados en un medio permanente, como un disco duro o una memoria flash. Ya se vio cómo abrir y leer un archivo en Sección 9.1.
Para escribir un archivo, debe abrirlo usando el modo "w" (de write) como segundo parámetro:
julia> fout = open("salida.txt", "w")
IOStream(<file salida.txt>)Si el archivo ya existe, abrirlo en modo de escritura borra los datos antiguos y comienza de nuevo, ¡así que tenga cuidado!. Si el archivo no existe, se crea uno nuevo. open devuelve un objeto de archivo y la función write escribe datos en el archivo.
julia> linea1 = "El Cid convoca a sus vasallos;\n";
julia> write(fout, linea1)
31El valor de retorno es el número de caracteres que se escribieron. El objeto de archivo fout lleva el registro de dónde se quedó por última vez, por lo que si llama a write nuevamente, esta agrega nuevos datos al final del archivo.
julia> linea2 = "éstos se destierran con él.\n";
julia> write(fout, linea2)
30Cuando el usuario haya terminado de escribir, debe cerrar el archivo.
julia> close(fout)Si no cierra el archivo, este se cierra cuando finaliza el programa.
Formateo
El argumento de write tiene que ser una cadena, por lo que si queremos poner otros valores en un archivo, tenemos que convertirlos a cadenas. La forma más fácil de hacerlo es con la función string o con interpolación de cadenas:
julia> fout = open("salida.txt", "w")
IOStream(<file salida.txt>)
julia> write(fout, string(150))
3Otra alternativa es utilizar la familia de funciones de print(ln).
julia> camellos = 42
42
julia> println(fout, "He visto $camellos camellos.")|
Observación
|
Una alternativa más potente es la macro |
Nombre de Archivo y Ruta
Los archivos están organizados en directorios (también llamados "carpetas"). Cada programa en ejecución tiene su propio "directorio actual", que es el directorio que usará por defecto para para la mayoría de las operaciones. Por ejemplo, cuando abre un archivo para leer, Julia lo busca en el directorio actual.
La función pwd (en inglés "print working directory") devuelve el nombre del directorio actual:
julia> cwd = pwd()
"/home/ben"cwd significa "directorio del trabajo actual" (en inglés “current working directory”). El resultado en este ejemplo es /home/ben, que es el directorio de inicio de un usuario llamado ben.
Una cadena como "/home/ben" que identifica un archivo o directorio se llama ruta o path.
Un nombre de archivo simple, como memo.txt también se considera una ruta aunque es una ruta relativa porque comienza en el directorio actual. Si el directorio actual es /home/ben, el nombre de archivo memo.txt se refiere a /home/ben/memo.txt.
Una ruta que comienza con / no depende del directorio actual. Este tipo de ruta se llama ruta absoluta. Para encontrar la ruta absoluta de un archivo, puede usar abspath:
julia> abspath("memo.txt")
"/home/ben/memo.txt"Julia también tiene otras funciones para trabajar con nombres de archivo y rutas. Por ejemplo, ispath comprueba si existe un archivo o directorio:
julia> ispath("memo.txt")
trueSi existe, isdir comprueba si es un directorio:
julia> isdir("memo.txt")
false
julia> isdir("/home/ben")
trueDel mismo modo, isfile comprueba que se trate de un archivo.
readdir devuelve un arreglo de los archivos (y otros directorios) en el directorio dado:
julia> readdir(cwd)
3-element Array{String,1}:
"memo.txt"
"musica"
"fotos"Para mostrar el comportamiento de estas funciones, el siguiente ejemplo "recorre" un directorio, imprime los nombres de todos los archivos y se llama a sí misma, de manera recursiva, en todos los directorios.
function recorrer(nombredir)
for nombre in readdir(nombredir)
ruta = joinpath(nombredir, nombre)
if isfile(ruta)
println(ruta)
else
recorrer(ruta)
end
end
endjoinpath toma un directorio y un nombre de archivo y los une en una ruta completa.
|
Observación
|
Julia tiene una función integrada llamada |
Captura de Excepciones
Muchas cosas pueden salir mal al intentar leer y escribir archivos. Al intentar abrir un archivo que no existe, se obtiene un SystemError:
julia> fin = open("archivo_malo")
ERROR: SystemError: opening file "archivo_malo": No such file or directorySi el usuario intenta abrir un archivo pero no tiene permiso para acceder a él, obtiene el error de sistema "Permission denied" (Permiso denegado).
Para evitar estos errores se podrían usar funciones como ispath e isfile pero tomaría mucho tiempo y líneas de código verificar todas las posibilidades.
Es más fácil intentar lidiar con los problemas a medida que ocurren, que es exactamente lo que hace la sentencia try. La sintaxis es similar a una sentencia if:
try
fin = open("archivo_malo.txt")
catch exc
println("Algo salió mal: $exc")
endJulia comienza ejecutando el bloque try. Si nada falla, se saltará el bloque catch y finalizará. Si ocurre una excepción, Julia saltará fuera del bloque try y ejecutará el bloque catch.
Gestionar una excepción con try recibe el nombre de capturar una excepción. En este ejemplo, el bloque catch muestra un mensaje de error que no es muy útil. En general, capturar una excepción da la oportunidad de corregir el problema, volverlo a intentar o, al menos, terminar el programa con elegancia.
Cuando el código realiza cambios de estado o usa recursos, como archivos, generalmente se deben hacer ciertas cosas al finalizar la programación del código, como por ejemplo cerrar los archivos. Las excepciones pueden complicar esta tarea, ya que se podría salir antes de lo esperado de un bloque de código. La palabra reservada finally permite ejecutar un código al salir de un bloque de código determinado, independientemente de cómo salga:
f = open("salida.txt")
try
linea = readline(f)
println(linea)
finally
close(f)
endEn este ejemplo, la función close siempre se ejecutará.
Bases de datos
Una base de datos es un archivo que está organizado para almacenar datos. La mayoría de las bases de datos están organizadas como diccionarios, en el sentido de que realizan asociaciones entre claves y valores. La diferencia más importante entre un diccionario y una base de datos, es que la base de datos se encuentra en el disco (u otro almacenamiento permanente), de modo que su contenido se conserva después de que el programa haya finalizado.
IntroAJulia proporciona una interfaz para GDBM (GNU dbm), que permite crear y actualizar archivos de base de datos. A modo de ejemplo, se crea una base de datos que contiene pies de foto para archivos de imagen.
Abrir una base de datos es similar a abrir otros archivos:
julia> using IntroAJulia
julia> bd = DBM("piedefoto", "c")
DBM(<piedefoto>)El modo "c" significa que la base de datos debe crearse si no existe. El resultado es un objeto de base de datos que se puede usar (para la mayoría de las operaciones) como un diccionario.
Cuando se crea un nuevo elemento, GDBM actualiza el archivo de base de datos:
julia> bd["luismi.png"] = "Foto de Luis Miguel."
"Foto de Luis Miguel."Cuando accede a uno de los elementos, GDBM lee el archivo:
julia> bd["luismi.png"]
"Foto de Luis Miguel."Si realiza otra asignación a una clave existente, GDBM reemplaza el valor anterior:
julia> bd["luismi.png"] = "Foto de Luis Miguel cantando."
"Foto de Luis Miguel cantando."
julia> bd["luismi.png"]
"Foto de Luis Miguel cantando."Algunas funciones que tienen un diccionario como argumento, con claves y valores, no funcionan con objetos de base de datos. No obstante, la iteración con un bucle for sí:
for (clave, valor) in bd
println(clave, ": ", valor)
endAl igual que con otros archivos, debe cerrar la base de datos cuando haya terminado:
julia> close(bd)Serialización
Una limitación de GDBM es que las claves y los valores deben ser cadenas o conjuntos de bytes. Si intenta utilizar cualquier otro tipo, se producirá un error.
Las funciones serialize y deserialize pueden ser útiles. Traducen casi cualquier tipo de objeto en un arreglo de bytes (un iobuffer) adecuado para el almacenamiento en una base de datos y luego traducen los arreglos de bytes nuevamente en objetos:
julia> using Serialization
julia> io = IOBuffer();
julia> t = [1, 2, 3];
julia> serialize(io, t)
24
julia> print(take!(io))
UInt8[0x37, 0x4a, 0x4c, 0x0a, 0x04, 0x00, 0x00, 0x00, 0x15, 0x00, 0x08, 0xe2, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x02, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x03, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00]El formato no es intuitivo para nosotros pero es fácil de interpretar para Julia. deserialize reconstituye el objeto:
julia> io = IOBuffer();
julia> t1 = [1, 2, 3];
julia> serialize(io, t1)
24
julia> s = take!(io);
julia> t2 = deserialize(IOBuffer(s));
julia> print(t2)
[1, 2, 3]serialize y deserialize escriben y leen desde un objeto iobuffer que representa un I/O stream en memoria. La función take! recupera el contenido del iobuffer como un arreglo de bytes y reestablece el iobuffer a su estado inicial.
Aunque el nuevo objeto tiene el mismo valor que el anterior, no es (en general) el mismo objeto:
julia> t1 == t2
true
julia> t1 ≡ t2
falseEn otras palabras, la serialización y luego la deserialización tienen el mismo efecto que copiar el objeto.
Esto se puede usar para almacenar valores que no sean cadenas en una base de datos.
|
Observación
|
De hecho, el almacenamiento de valores que no son cadenas en una base de datos es tan común que se ha encapsulado en un paquete llamado |
Objetos de Comando
La mayoría de los sistemas operativos proporcionan una interfaz de línea de comandos, también conocida como shell. Las shells generalmente proporcionan comandos para navegar por el sistema de archivos y ejecutar aplicaciones. Por ejemplo, en Unix puede cambiar los directorios con cd, mostrar el contenido de un directorio con ls e iniciar un navegador web escribiendo (por ejemplo) firefox.
Cualquier programa que se pueda iniciar desde la shell también puede iniciarse desde Julia usando un objeto de comando:
julia> cmd = `echo hola`
`echo hola`Las comillas invertidas se usan para delimitar el comando.
La función run ejecuta el comando:
julia> run(cmd);
holahola es la salida del comando echo, enviado a STDOUT. La función run devuelve un objeto de proceso y genera un ErrorException si el comando externo no se ejecuta correctamente.
Si se desea leer la salida del comando externo, se puede usar read en su lugar:
julia> a = read(cmd, String)
"hola\n"Por ejemplo, la mayoría de los sistemas Unix tienen un comando llamado md5sum o md5 que lee el contenido de un archivo y calcula una "suma de verificación". Puede leer sobre Md5 en https://en.wikipedia.org/wiki/Md5. Este comando proporciona una manera eficiente de verificar si dos archivos tienen el mismo contenido. La probabilidad de que diferentes contenidos produzcan la misma suma de comprobación es muy pequeña.
Puede usar un objeto de comando para ejecutar md5 desde Julia y obtener el resultado:
julia> nombrearchivo = "salida.txt"
"salida.txt"
julia> cmd = `md5 $nombrearchivo`
`md5 salida.txt`
julia> res = read(cmd, String)
ERROR: IOError: could not spawn `md5 salida.txt`: no such file or directory (ENOENT)Modulos
Supongamos que tenemos un archivo llamado "wc.jl" con el siguiente código:
function contarlineas(nombrearchivo)
conteo = 0
for linea in eachline(nombrearchivo)
conteo += 1
end
conteo
end
print(contarlineas("wc.jl"))Si ejecuta este programa, se leen las líneas de código y se imprime el número de líneas en el archivo, que es 9. También puede incluirlo en REPL de esta manera:
julia> include("wc.jl")
9Los módulos permiten crear espacios de trabajo separados, es decir, nuevos global scopes (ámbitos de tipo global). Una sentencia tiene global scope si tiene efecto en todo el programa.
Un módulo comienza con la palabra reservada module y termina con end. Al usar módulos, se evitan los conflictos de nombres entre sus propias definiciones de nivel superior y las que se encuentran en el código de otra persona. import permite controlar qué nombres de otros módulos están visibles y export especifica cuáles de sus nombres son públicos, es decir, aquellos que se pueden usar fuera del módulo sin tener el prefijo del nombre del módulo.
module ContarLineas
export contarlineas
function contarlineas(nombrearchivo)
conteo = 0
for linea in eachline(nombrearchivo)
conteo += 1
end
conteo
end
endEl módulo ContarLineas proporciona la función contarlineas:
julia> using ContarLineas
julia> contarlineas("wc.jl")
11Ejercicio 14-1
Escriba este ejemplo en un archivo llamado wc.jl, inclúyalo en REPL (con include) y escriba using ContarLineas.
|
Aviso
|
Si importa un módulo que ya se ha importado, Julia no hace nada. No se vuelve a leer el archivo, incluso si ha sido modificado. Si desea volver a cargar un módulo, debe reiniciar REPL. El paquete |
Depuración
Al leer y escribir archivos, el usuario puede tener problemas con los espacios en blanco. Estos errores pueden ser difíciles de depurar porque los espacios, las tabulaciones y las nuevas líneas son generalmente invisibles:
julia> s = "1 2\t 3\n 4";
julia> println(s)
1 2 3
4Las funciones integradas repr o dump pueden ser de ayuda. Toman cualquier objeto como argumento y devuelven una representación de tipo cadena del objeto.
"1 2\t 3\n 4"
julia> repr(s)
"\"1 2\\t 3\\n 4\""
julia> dump(s)
String "1 2\t 3\n 4"Esto puede ser útil para la depuración.
Otro problema con el que es fácil encontrarse es que en diferentes sistemas operativos se usan diferentes caracteres para indicar el final de una línea. Algunos sistemas usan una nueva línea, representada por \n. Otros usan un carácter de retorno \r. Algunos usan ambos. Si un archivo es usado en diferentes sistemas, estas inconsistencias podrían causar problemas.
Para la mayoría de los sistemas, hay aplicaciones para convertir de un formato a otro. Puede encontrarlas (y leer más sobre este tema) en https://en.wikipedia.org/wiki/Newline. O, por supuesto, podría escribir una usted mismo.
Glosario
- persistente
-
Perteneciente a un programa que se ejecuta indefinidamente y mantiene al menos algunos de sus datos en almacenamiento permanente.
- archivo de texto
-
Una secuencia de caracteres almacenados en almacenamiento permanente, tal como en un disco duro.
- directorio
-
Una colección de archivos con nombre, también llamada carpeta.
- ruta
-
Una cadena que identifica a un archivo.
- ruta relativa
-
Una ruta que comienza en el directorio actual.
- ruta absoluta
-
Una ruta que comienza en el directorio superior del sistema de archivos.
- capturar (catch)
-
Evitar que una excepción haga terminar un programa, utilizando las sentencias
try ... catch ... finally. - base de datos
-
Un archivo cuyo contenido está organizado como un diccionario con claves que corresponden a valores.
- shell
-
Un programa que permite a los usuarios escribir comandos y luego ejecutarlos iniciando otros programas.
- objeto de comando
-
Un objeto que representa un comando de shell. Esto permite que un programa de Julia ejecute comandos y lea los resultados.
Ejercicios
Ejercicio 14-2
Escriba una función llamada sed que tome como argumentos una cadena de patrones, una cadena de reemplazo y dos nombres de archivo. La función debe leer el primer archivo y escribir el contenido en el segundo archivo (creándolo si es necesario). Si la cadena de patrones aparece en algún lugar del archivo, debe reemplazarse con la cadena de reemplazo.
Si se produce un error al abrir, leer, escribir o cerrar los archivos, su programa debe detectar la excepción, imprimir un mensaje de error y terminar.
Ejercicio 14-3
Si hizo Sección 12.10.2, recordará que debía crear un diccionario que asociaba una cadena ordenada de letras al conjunto de palabras que se podía deletrear con esas letras. Por ejemplo, "cuaderno" estaba asociado al arreglo ["cuaderno", "educaron", "encuadro"].
Escriba un módulo que importe conjuntoanagramas y proporcione dos nuevas funciones: almacenaranagramas, que almacena el diccionario de anagramas usando JLD2 (vea https://github.com/JuliaIO/JLD2.jl); y leeranagramas, que busca una palabra y devuelve un arreglo de sus anagramas.
Ejercicio 14-4
En una gran colección de archivos MP3, puede haber más de una copia de la misma canción, almacenada en diferentes directorios o con diferentes nombres de archivo. El objetivo de este ejercicio es buscar duplicados.
-
Escriba un programa que busque un directorio y todos sus subdirectorios, de forma recursiva, y devuelva un arreglo de rutas completas para todos los archivos con un sufijo dado (como .mp3).
-
Para reconocer duplicados, puede usar
md5sumomd5para calcular una "suma de verificación" para cada archivo. Si dos archivos tienen la misma suma de verificación, probablemente tengan el mismo contenido. -
Para verificarlo, puede usar el comando de Unix
diff.
15. Estructuras y Objetos
A esta altura, ya debe saber cómo usar funciones para tener un código más organizado y cómo usar los tipos integrados de Julia para organizar sus datos. El siguiente paso es aprender a construir sus propios tipos para organizar tanto el código como los datos. Este es un gran tema y, por lo tanto, tomará un par de capítulos abarcar todo.
Tipos Compuestos
Se han utilizado muchos tipos integrados en Julia y ahora se va a definir un nuevo tipo. A modo de ejemplo, se crea un tipo llamado Punto que representa un punto en un espacio bidimensional.
En notación matemática, los puntos suelen escribirse entre paréntesis con una coma que separa las coordenadas. Por ejemplo, \(\left(0,0\right)\) representa el origen y \(\left(x,y\right)\) representa el punto localizado \(x\) unidades a la derecha y \(y\) unidades hacia arriba del origen.
Hay varias formas en que se podrían representar puntos del plano cartesiano en Julia:
-
Almacenando las coordenadas por separado en dos variables,
xey. -
Almacenando las coordenadas como elementos de un arreglo o tupla.
-
Creando un nuevo tipo para representar puntos como objetos.
Crear un nuevo tipo exige un poco más de esfuerzo que las otras dos opciones pero tiene algunas ventajas, como pronto se verá.
Un tipo compuesto definido por el programador también se denomina estructura (struct en inglés). La definición de estructura de un punto se ve así:
struct Punto
x
y
endEl encabezado indica que la nueva estructura se llama Punto. El cuerpo define los atributos o campos de la estructura. La estructura de Punto tiene dos campos: x e y.
Una estructura es como una fábrica que crea objetos. Para crear un punto, se debe llamar a Punto como si fuera una función que tiene como argumentos los valores de los campos. Cuando Punto se usa como una función, se llama constructor.
julia> p = Punto(3.0, 4.0)
Punto(3.0, 4.0)El valor de retorno es una referencia a un objeto Punto, el cual es asignado a p.
La creación de un nuevo objeto se llama instanciación, y el objeto creado es una instancia del tipo.
Cuando se imprime una instancia Julia dice a qué tipo pertenece y cuáles son los valores de los atributos.
Cada objeto es una instancia de algún tipo, por lo que "objeto" e "instancia" son intercambiables. No obstante, en este capítulo se utiliza "instancia" para indicar que se está hablando de un tipo definido por el programador.
Un diagrama de estado que muestra un objeto y sus atributos se denomina diagrama de objeto (ver Figura 20).
Las Estructuras son Inmutables
Puede obtener los valores de los campos utilizando la notación .:
julia> x = p.x
3.0
julia> p.y
4.0La expresión p.x significa: "Vaya al objeto al que se apunta p y obtenga el valor de x". En el ejemplo, se asigna ese valor a una variable llamada x. No hay conflicto entre la variable x y el atributo x.
Puede usar esa notación de punto como parte de cualquier expresión. Por ejemplo:
julia> distancia = sqrt(p.x^2 + p.y^2)
5.0Sin embargo, las estructuras son inmutables por defecto y después de la construcción los campos no pueden cambiar su valor:
julia> p.y = 1.0
ERROR: setfield! immutable struct of type Punto cannot be changedEsto puede parecer extraño al principio pero tiene varias ventajas:
-
Puede ser más eficiente.
-
No es posible violar las invariantes (requisitos que deberían cumplirse en todos los objetos, en todo momento) de los constructores de un tipo compuesto (ver Sección 17.4).
-
El código que usa objetos inmutables puede ser más fácil de entender.
Estructuras Mutables
De ser necesario, se pueden declarar tipos compuestos mutables con la palabra reservada mutable struct. A continuación se muestra la definición de un punto mutable:
mutable struct MPunto
x
y
endPuede asignar valores a una instancia de una estructura mutable utilizando notación de punto (.):
julia> blanco = MPunto(0.0, 0.0)
MPunto(0.0, 0.0)
julia> blanco.x = 3.0
3.0
julia> blanco.y = 4.0
4.0Rectángulos
A veces, decidir cuáles deberían ser los campos de un objeto es fácil, pero en otros casos no. Por ejemplo, imagine que se quiere un tipo que represente un rectángulo. ¿Qué campos usaría para especificar la ubicación y el tamaño de un rectángulo? Puede ignorar el ángulo. Para simplificar las cosas, suponga que el rectángulo es vertical u horizontal.
Hay al menos dos posibilidades:
-
Puede especificar una esquina del rectángulo (o el centro), el ancho y la altura.
-
Puede especificar dos esquinas opuestas.
Es difícil decir que una opción es mejor que la otra, por lo que implementaremos la primera, a modo de ejemplo.
"""
Representa un rectángulo.
atributos: ancho, alto, esquina.
"""
struct Rectangulo
ancho
alto
esquina
endEl texto escrito entre comillas triples es llamado cadena de documentación (o docstring), y permite documentar. La documentación es el acto de comentar convenientemente cada una de las partes que tiene el programa.
En este ejemplo, la cadena de documentación (o docstring) enumera los atributos. Los atributos ancho y alto son números y esquina es un objeto Punto que especifica la esquina inferior izquierda.
Para representar un rectángulo debe crear una instancia del tipo Rectangulo:
julia> origen = MPunto(0.0, 0.0)
MPunto(0.0, 0.0)
julia> caja = Rectangulo(100.0, 200.0, origen)
Rectangulo(100.0, 200.0, MPunto(0.0, 0.0))Figura 21 muestra el estado de este objeto. Un objeto es embebido si es atributo de otro objeto. Debido a que el atributo esquina se refiere a un objeto mutable, se dibuja fuera del objeto Rectangulo.
Instancias como Argumentos
Podemos pasar una instancia como argumento de la manera habitual. Por ejemplo:
function imprimirpunto(p)
println("($(p.x), $(p.y))")
endimprimirpunto toma un Punto como argumento y lo muestra en notación matemática. Puede llamar a imprimirpunto con un argumento p:
julia> imprimirpunto(blanco)
(3.0, 4.0)Ejercicio 15-1
Escriba una función llamada distanciaentrepuntos que tome dos puntos como argumentos y devuelva la distancia entre ellos.
Si un objeto de estructura mutable se pasa a una función como argumento, la función puede modificar los campos del objeto. Por ejemplo, moverpunto! toma un objeto mutable Punto y dos números, dx y dy, los cuales suma a los atributos x e y de Punto, respectivamente:
function moverpunto!(p, dx, dy)
p.x += dx
p.y += dy
nothing
endAquí hay un ejemplo que muestra como funciona:
julia> origen = MPunto(0.0, 0.0)
MPunto(0.0, 0.0)
julia> moverpunto!(origen, 1.0, 2.0)
julia> origen
MPunto(1.0, 2.0)Dentro de la función, p es un alias de origen, por lo que cuando la función modifica p, origen también cambia.
Al pasar un objeto inmutable Punto a moverpunto! se produce un error:
julia> moverpunto!(p, 1.0, 2.0)
ERROR: setfield! immutable struct of type Punto cannot be changedSin embargo, se puede modificar el valor de un atributo mutable de un objeto inmutable. Por ejemplo, moverrectangulo! tiene como argumentos un objeto Rectangulo y dos números, dx y dy. Esta función usa moverpunto! para mover la esquina del rectángulo:
function moverrectangulo!(rect, dx, dy)
moverpunto!(rect.esquina, dx, dy)
endAhora p en moverpunto! es un alias para rect.esquina, por lo que cuando p se modifica, rect.esquina también cambia:
julia> caja
Rectangulo(100.0, 200.0, MPunto(0.0, 0.0))
julia> moverrectangulo!(caja, 1.0, 2.0)
julia> caja
Rectangulo(100.0, 200.0, MPunto(1.0, 2.0))|
Aviso
|
No puede reasignar un atributo mutable de un objeto inmutable: |
Instancias como Valores de Retorno
Las funciones pueden devolver instancias. Por ejemplo, encontrarcentro toma un Rectangulo como argumento y devuelve un Punto que contiene las coordenadas del centro del rectángulo:
function encontrarcentro(rect)
Punto(rect.esquina.x + rect.ancho / 2, rect.esquina.y + rect.alto / 2)
endLa expresión rect.corner.x significa: “Vaya al objeto al que rect apunta y seleccione el atributo llamado esquina. Luego vaya a ese objeto y seleccione el atributo llamado x""".
A continución se observa un ejemplo que toma caja como argumento y asigna el Punto resultante a centro:
julia> centro = encontrarcentro(caja)
Punto(51.0, 102.0)Copiado
El uso de alias puede hacer que un programa sea difícil de leer ya que los cambios hechos en un lugar pueden tener efectos inesperados en otro lugar. Es difícil estar al tanto de todas las variables a las que puede apuntar un objeto dado.
Copiar un objeto es, muchas veces, una alternativa a la creación de un alias. Julia provee una función llamada copy que puede duplicar cualquier objeto:
julia> p1 = MPunto(3.0, 4.0)
MPunto(3.0, 4.0)
julia> p2 = deepcopy(p1)
MPunto(3.0, 4.0)
julia> p1 ≡ p2
false
julia> p1 == p2
falseEl operador ≡ indica que p1 y p2 no son el mismo objeto, lo cual es esperable. Lo que no es del todo esperable es que == no devuelva true, aunque estos puntos contengan los mismos datos. Resulta que para los objetos mutables, el comportamiento predeterminado del operador == es el mismo que el operador ===, es decir, comprueba la identidad del objeto, no la equivalencia del objeto. Esto se debe a que Julia no sabe qué debería considerarse equivalente para los tipos compuestos mutables. Al menos no todavía.
Ejercicio 15-2
Cree una instancia de Punto, haga una copia y verifique la equivalencia y la igualdad de ambas. El resultado puede sorprenderlo, pero explica por qué el alias no es un problema para un objeto inmutable.
Depuración
Al comenzar a trabajar con objetos, es probable que encuentre algunas excepciones nuevas. Si intenta acceder a un campo que no existe, obtendrá:
julia> p = Punto(3.0, 4.0)
Punto(3.0, 4.0)
julia> p.z = 1.0
ERROR: type Punto has no field zSi no está seguro del tipo de un objeto, puede saberlo de la siguiente manera:
julia> typeof(p)
PuntoTambién puede usar isa para verificar si un objeto es una instancia de un tipo específico:
julia> p isa Punto
trueSi no está seguro de si un objeto tiene un atributo particular, puede usar la función fieldnames:
julia> fieldnames(Punto)
(:x, :y)o la función isdefined:
julia> isdefined(p, :x)
true
julia> isdefined(p, :z)
falseEl primer argumento puede ser cualquier objeto y el segundo argumento es el símbolo : seguido del nombre del atributo.
Glosario
- estructura
-
Un tipo compuesto.
- constructor
-
Una función con el mismo nombre que un tipo, que crea instancias de este tipo.
- instancia
-
Un objeto que pertenece a un tipo.
- instanciar
-
Crear un nuevo objeto.
- atributo o campo
-
Un valor con nombre asociado un objeto.
- objeto embebido
-
Un objeto que se almacena como atributo de otro objeto.
- deep copy o copia profunda
-
Copiar el contenido de un objeto, y cualquier objeto embebido en él y, a su vez, cualquier objeto embebido en ellos, y así sucesivamente. Implementado por la función
deepcopy. - diagrama de objeto
-
Un diagrama que muestra objetos, sus atributos y valores de atributos.
Ejercicios
Ejercicio 15-3
-
Escriba una definición de un tipo llamado
Circuloque tenga atributoscentroyradioy dóndecentrosea un objetoPuntoyradioun número. -
Cree una instancia de un objeto
Circuloque represente a un círculo con centro en \(\left(150, 100\right)\) y radio 75. -
Escriba una función llamada
puntoencirculoque tome un objetoCirculoy un objetoPuntoy devuelvatruesi el punto se encuentra dentro o en el límite del círculo. -
Escriba una función llamada
rectencirculoque tome un objetoCirculoy un objetoRectanguloy devuelvatruesi el rectángulo se encuentra completamente dentro o en el límite del círculo. -
Escriba una función llamada
sobreposicionrectcircque tome un objetoCirculoy un objetoRectanguloy devuelvatruesi alguna de las esquinas del rectángulo cae dentro del círculo. Una versión más desafiante es escribir una función que devuelvatruesi alguna parte del rectángulo (no necesariamente una esquina) cae dentro del círculo.
Ejercicio 15-4
-
Escriba una función llamada
dibujarrectque tome como argumentos un objeto turtle y un objetoRectángulo, y use turtle para dibujar el rectángulo. Consulte el Capítulo 4 para ver ejemplos que usen objetosTurtle. -
Escriba una función llamada
dibujarcirculoque tome como argumentos un objetoTurtley un objetoCirculo, y dibuje el círculo.
16. Estructuras y Funciones
Ahora que se ha tratado cómo crear tipos compuestos, el siguiente paso es escribir funciones que tomen objetos definidos por el programador como parámetros y que devuelvan otros como resultados. En este capítulo también se presenta el "estilo de programación funcional" y dos nuevas formas de desarrollar programas.
Tiempo
Como otro ejemplo de tipo compuesto, se define una estructura llamada Hora que registra la hora del día. La definición de esta estructura se muestra a continuación:
"""
Representa la hora del día.
atributos: hora, minuto, segundo
"""
struct Hora
hora
minuto
segundo
endObservación: Time es una palabra reservada de Julia.
julia> tiempo = Hora(11, 59, 30)
Hora(11, 59, 30)El diagrama de objeto para el objeto Hora luce así Figura 22.
Ejercicio 16-1
Escriba una función llamada imprimirhora que tome un objeto Hora y lo imprima con el formato hora:minuto:segundo. Printf, de la macro @printf del módulo StdLib, permite imprimir un número entero con el formato "%02d", es decir, utilizando al menos dos dígitos, incluido un cero inicial si es necesario.
Ejercicio 16-2
Escriba una función booleana llamada estadespues que tome dos objetos Hora: t1 y t2 y devuelva true si la hora t1 está después que t2 y false de lo contrario. Desafío: no use sentencias if.
Funciones Puras
En las siguientes secciones se escriben dos versiones de una función que calcula la suma de horas. La primera versión muestra un tipo de función llamado función pura y la segunda un tipo llamado modificador. Además, estas versiones permitirán mostrar un nuevo plan de desarrollo de programas llamado desarrollo de prototipos, una forma de abordar un problema complejo comenzando con un prototipo simple y lidiando gradualmente con las complicaciones.
Este es un primer prototipo de la función sumahora:
function sumahora(t1, t2)
Hora(t1.hora + t2.hora, t1.minuto + t2.minuto, t1.segundo + t2.segundo)
endLa función crea un nuevo objeto Hora, inicializa sus atributos y devuelve una referencia al nuevo objeto. A esto se le llama función pura porque no modifica ninguno de los objetos que se le pasan como argumento, y no tiene efectos (como mostrar un valor o tomar una entrada del usuario) más que devolver un valor.
Para probar esta función, se crean dos objetos Hora: inicio, que contiene la hora de inicio de una película, como Roma, y duracion, que contiene la duración de la película, que es dos horas y 15 minutos.
sumahora calcula cuándo se terminará la película.
imprimirhora (generic function with 1 method)
julia> inicio = Hora(9, 50, 0);
julia> duracion = Hora(2, 15, 0);
julia> finaliza = sumahora(inicio, duracion);
julia> imprimirhora(finaliza)
11:65:00El resultado 11:65:00 no es lo que se buscaba. El problema es que esta función no considera los casos en los que el número de segundos o minutos suma más que sesenta. Cuando esto ocurre, debemos "acarrear" (como en una suma) los segundos sobrantes a la columna de los minutos o los minutos extras a la columna de las horas. He aquí una versión corregida de la función:
function sumahora(t1, t2)
segundo = t1.segundo + t2.segundo
minuto = t1.minuto + t2.minuto
hora = t1.hora + t2.hora
if segundo >= 60
segundo -= 60
minuto += 1
end
if minuto >= 60
minuto -= 60
hora += 1
end
Hora(hora, minuto, segundo)
endAunque esta función es correcta, es muy larga. Más adelante se explorará una alternativa más corta.
Modificadores
Hay veces en las que es útil que una función modifique uno o más de los objetos que recibe como parámetros. En ese caso, los cambios son visibles en el nivel en donde se ubica la sentencia de llamada. Estas funciones se llaman modificadores.
La función incrementar!, que agrega un número dado de segundos a un objeto Hora, puede escribirse naturalmente como un modificador. Aquí se muestra un prototipo de la función:
function incrementar!(tiempo, segundos)
tiempo.segundo += segundos
if tiempo.segundo >= 60
tiempo.segundo -= 60
tiempo.minute += 1
end
if tiempo.minuto >= 60
tiempo.minuto -= 60
tiempo.hora += 1
end
endLa primera línea realiza la suma de los segundos y las restantes se ocupan de los casos especiales vistos anteriormente.
¿Es correcta esta función? ¿Qué ocurre si el parámetro segundos es mucho mayor que sesenta?
En tal caso, no es suficiente con acarrear una vez, debemos seguir haciéndolo hasta que tiempo.segundo sea menor que sesenta. Una solución es sustituir las sentencias if por sentencias while. Esta función sería correcta pero no es la solución más eficiente.
Ejercicio 16-3
Escriba una versión correcta de incrementar! sin bucles.
Todo lo que se pueda hacer con modificadores también puede lograrse con funciones puras. De hecho, algunos lenguajes de programación solo permiten funciones puras. Hay ciertas evidencias de que los programas que usan funciones puras son más rápidos de desarrollar y menos propensos a errores que los programas que usan modificadores. Sin embargo, a veces los modificadores son útiles y en algunos casos los programas funcionales (es decir, con funciones puras) tienden a ser menos eficientes.
En general, recomendamos que escriba funciones puras siempre que sea razonable y recurra a los modificadores sólo si hay una ventaja convincente. Este enfoque podría llamarse estilo de programación funcional.
Ejercicio 16-4
Escriba una versión "pura" de incrementar! que cree y devuelva un nuevo objeto Hora en vez de modificar el parámetro.
Desarrollo de prototipos frente a la planificación
El desarrollo de programas que veremos ahora se llama “desarrollo de prototipos”. En cada una de las funciones anteriores, escribimos un prototipo que realizaba el cálculo básico y luego lo probamos sobre unos cuantos casos, corrigiendo los errores a medida que iban apareciendo.
Este enfoque puede ser efectivo, especialmente si aún no tiene un conocimiento profundo del problema. No obstante, las correcciones incrementales pueden generar código innecesariamente complicado (que considere muchos casos especiales) y poco confiable (es difícil saber si ha encontrado todos los errores).
Una alternativa es el desarrollo planificado, en el que la comprensión del problema en profundidad puede facilitar en gran medida la programación. En el caso de sumahora, se puede ver un objeto Hora como ¡un número de tres dígitos en base 60 (vea https://en.wikipedia.org/wiki/Sexagesimal )!. El atributo segundo es la “columna de unidades”, el atributo minuto es la “columna de los sesentas” y el atributo hora es la “columna de los tres mil seiscientos”.
Cuando se escribía sumahora e incrementar!, efectivamente se estaba sumando en base 60, por eso se tuvo que "acarrear" de una columna a la siguiente.
Esta observación sugiere otro enfoque para el problema: se pueden convertir los objetos Hora en enteros y aprovechar el hecho de que la computadora sabe realizar aritmética con enteros.
La siguiente función convierte un objeto Hora en un entero:
function horaaentero(tiempo)
minutos = tiempo.hora * 60 + tiempo.minuto
segundos = minutos * 60 + tiempo.segundo
endAhora, para convertir un entero en un objeto Hora (recuerde que divrem divide el primer argumento por el segundo, y devuelve el cociente y el resto como una tupla):
function enteroahora(segundos)
(minutos, segundo) = divrem(segundos, 60)
hora, minuto = divrem(minutos, 60)
Hora(hora, minuto, segundo)
endPuede que tenga que pensar un poco y realizar algunas pruebas para convencerse de que estas funciones son correctas. Una forma de probarlas es verificar que horaaenteroenteroahora(x == x para muchos valores de x. Este es un ejemplo de prueba de consistencia.
Una vez que esté convencido, puede usar estas funciones para reescribir sumahora:
function sumahora(t1, t2)
segundos = horaaentero(t1) + horaaentero(t2)
enteroahora(segundos)
endEsta versión es más corta que la original y más fácil de verificar.
Ejercicio 16-5
Reescriba incrementar! usando horaaentero y enteroahora.
Convertir de base 60 a base 10, y viceversa, es más difícil que solo trabajar con los tiempos. El cambio de base es más abstracto pero la intuición humana para tratar con las horas es mejor.
Si al usuario se le ocurre tratar los tiempos como números de base 60 e invierte un poco de tiempo en escribir las funciones de conversión (horaaentero y enteroahora), obtiene un programa más corto, fácil de leer y depurar y confiable.
El cambio de base también hace que sea más fácil añadir funcionalidades posteriormente. Por ejemplo, imagine restar dos Horas para hallar el intervalo entre ellas. El enfoque simple sería implementar una resta con "préstamo" pero usar funciones de conversión sería más fácil y con mayor probabilidad correcto.
Irónicamente, a veces hacer un poblema más complejo (o más general) lo hace más fácil porque hay menos casos especiales y por lo tanto, el margen de error es menor.
Depuración
Un objeto Hora está bien definido si los valores de minuto y segundo están entre 0 y 60 (incluido 0 pero no 60) y si hora es positivo. hora y minuto deben ser valores enteros, pero se podría permitir que segundo sea fraccional.
Los requisitos como estos se denominan invariantes porque siempre deben ser verdaderos. Dicho de otra manera, si no son ciertos, algo está mal.
Escribir código para verificar invariantes puede ayudar a detectar errores y encontrar sus causas. Por ejemplo, podría tener una función como eshoravalida que tome un objeto Hora y devuelva false si viola una invariante:
function eshoravalida(tiempo)
if tiempo.hora < 0 || tiempo.minuto < 0 || tiempo.segundo < 0
return false
end
if tiempo.minuto >= 60 || tiempo.segundo >= 60
return false
end
true
endAl comienzo de cada función, puede verificar los argumentos para asegurarse de que sean válidos:
function sumahora(t1, t2)
if !eshoravalida(t1) || !eshoravalida(t2)
error("objeto Hora en sumahora es inválido")
end
segundos = horaaentero(t1) + horaaentero(t2)
enteroahora(segundos)
endO podría usar una macro @assert, que verifica un invariante dado y genera una excepción si falla:
function sumahora(t1, t2)
@assert(eshoravalida(t1) && eshoravalida(t2), "objeto Hora en sumahora es inválido")
segundos = horaaentero(t1) + horaaentero(t2)
enteroahora(segundos)
endLas macros @assert son útiles porque permiten distinguir el código que trata condiciones normales del código que verifica los errores.
Glosario
- desarrollo de prototipos
-
Una forma de desarrollar programas que involucra generar un prototipo del programa, hacer pruebas y corregir errores a medida que son encontrados.
- desarrollo planificado
-
Una forma de desarrollar programas que implica una profunda comprensión del problema y más planificación que desarrollo incremental o desarrollo de prototipos.
- función pura
-
Una función que no modifica los objetos que recibe como parámetros. La mayoría de las funciones puras son productivas.
- modificador
-
Una función que modifica uno o más de los objetos que recibe como parámetros. La mayoría de los modificadores son nulos, es decir, entregan resultado
nothing. - estilo funcional de programación
-
Un estilo de programación en el que la mayoría de las funciones son puras.
- invariante
-
Una condición que nunca debería cambiar durante la ejecución de un programa.
Ejercicios
Ejercicio 16-6
Escriba una función llamada multhora que tome un objeto Hora y un número, y devuelva un nuevo objeto Hora que contenga el producto entre Hora original y el número.
Luego use multhora para escribir una función que tome un objeto Hora que represente el tiempo de duración de una carrera, y un número que represente la distancia y devuelva un objeto Hora que represente el ritmo promedio (minutos por kilómetro).
Ejercicio 16-7
Julia proporciona objetos de tiempo similares a los objetos Hora de este capítulo, pero que tienen un amplio conjunto de funciones y operadores. Lea la documentación en https://docs.julialang.org/en/v1/stdlib/Dates/.
-
Escriba un programa que tome la fecha actual e imprima el día de la semana.
-
Escriba un programa que tome como entrada una fecha de cumpleaños e imprima la edad del usuario y la cantidad de días, horas, minutos y segundos hasta su próximo cumpleaños.
-
Para dos personas nacidas en días diferentes, hay un día en que una tiene el doble de edad que la otra. Ese es su Día Doble. Escriba un programa que tome dos cumpleaños y calcule su Día doble.
-
Desafío: Escriba una versión más general que calcule el día en que una persona es \(n\) veces mayor que la otra.
17. Dispatch Múltiple
Julia permite escribir código que puede funcionar con diferentes tipos. Esto se llama programación genérica.
En este capítulo se discutirá sobre las declaraciones de tipo en Julia. Además, se presentan los métodos, que son formas de implementar diferentes comportamientos en una función dependiendo del tipo de sus argumentos. Esto es conocido como dispatch múltiple.
Declaraciones de Tipo
El operador :: asocia anotaciones de tipo con expresiones y variables:
julia> (1 + 2) :: Float64
ERROR: TypeError: in typeassert, expected Float64, got a value of type Int64
julia> (1 + 2) :: Int64
3Esto ayuda a verificar que el programa funciona de la manera esperada.
El operador :: también se puede agregar al lado izquierdo de una asignación o como parte de una declaración.
julia> function devolverfloat()
x::Float64 = 100
x
end
devolverfloat (generic function with 1 method)
julia> x = devolverfloat()
100.0
julia> typeof(x)
Float64La variable x siempre es de tipo Float64, y su valor se convierte en un punto flotante si es necesario.
También se puede añadir una anotación de tipo al encabezado de una definición de función:
function sinc(x)::Float64
if x == 0
return 1
end
sin(x)/(x)
endEl valor de retorno de sinc siempre se convierte al tipo Float64.
En Julia, cuando se omiten los tipos, los valores pueden ser de cualquier tipo (Any).
Métodos
En Capítulo 16, definimos una estructura llamada Hora y en Sección 16.1, escribimos una función llamada imprimirhora:
using Printf
struct Hora
hora :: Int64
minuto :: Int64
segundo :: Int64
end
function imprimirhora(tiempo)
@printf("%02d:%02d:%02d", tiempo.hora, tiempo.minuto, tiempo.segundo)
endPara mejorar el rendimiento, se pueden (y deben) agregar las declaraciones de tipo a los atributos en una definición de estructura.
Para llamar a esta función, debe pasarle un objeto Hora como argumento:
julia> inicio = Hora(9, 45, 0)
Hora(9, 45, 0)
julia> imprimirhora(inicio)
09:45:00Para agregar un método a la función imprimirhora; con el fin de que esta solo acepte como argumento un objeto Hora, todo lo que hay que hacer es agregar :: seguido de Hora al argumento tiempo en la definición de función:
function imprimirhora(tiempo::Hora)
@printf("%02d:%02d:%02d", tiempo.hora, tiempo.minuto, tiempo.segundo)
endUn método es una definición de función con una especificación: imprimirhora tiene un argumento de tipo Hora.
Llamar a la función imprimirhora con un objeto Hora produce el mismo resultado que antes:
julia> imprimirhora(inicio)
09:45:00Se redefine el primer método sin la anotación de tipo ::, lo cual permite un argumento de cualquier tipo:
function imprimirhora(tiempo)
println("No sé cómo imprimir el tiempo del argumento.")
endSi se llama a la función imprimirhora con un objeto diferente de Hora, se obtendrá:
julia> imprimirhora(150)
No sé cómo imprimir el tiempo del argumento.Ejercicio 17-1
Reescriba horaaentero y enteroahora (de Sección 16.4) especificando el tipo de los argumentos.
enteroahora (generic function with 1 method)
Ejemplos Adicionales
Aquí hay una versión de la función incrementar (Ejercicio 16-5 de Sección 16.3) reescrita especificando el tipo de los argumentos:
function incrementar(tiempo::Hora, segundos::Int64)
segundos += horaaentero(tiempo)
enteroahora(segundos)
endTenga en cuenta que ahora incrementar es una función pura, no un modificador.
Así es como se llama a la función incrementar:
julia> inicio = Hora(9, 45, 0)
Hora(9, 45, 0)
julia> incrementar(inicio, 1337)
Hora(10, 7, 17)Si se colocan los argumentos en el orden incorrecto, se obtiene un error:
julia> incrementar(1337, inicio)
ERROR: MethodError: no method matching incrementar(::Int64, ::Hora)La especificación del método es incrementar(tiempo::Hora, segundos::Int64), no incrementar(segundos::Int64, tiempo::Hora).
Al reescribir estadespues (Ejercicio 16-2 de Sección 16.3) para que solo acepte objetos Hora se tiene:
function estadespues(t1::Hora, t2::Hora)
(t1.hora, t1.minuto, t1.segundo) > (t2.hora, t2.minuto, t2.segundo)
endHace falta destacar que los argumentos opcionales permiten definir múltiples métodos. Por ejemplo, esta definición:
function f(a=1, b=2)
a + 2b
endse traduce en los siguientes tres métodos:
f(a, b) = a + 2b
f(a) = f(a, 2)
f() = f(1, 2)Estas expresiones son definiciones válidas de métodos de Julia. Esta es una notación abreviada para definir funciones/métodos.
Constructores
Un constructor es una función especial que se llama para crear un objeto. Los métodos por defecto del constructor Hora tienen las siguientes especificaciones:
Hora(hora, minuto, segundo)
Hora(hora::Int64, minuto::Int64, segundo::Int64)También se pueden agregar métodos propios de constructores externos:
function Hora(tiempo::Hora)
Hora(tiempo.hora, tiempo.minuto, tiempo.segundo)
endEste método se llama constructor de copia porque el nuevo objeto Hora es una copia de su argumento.
Para imponer invariantes se necesitan métodos de constructor interno:
struct Hora
hora :: Int64
minuto :: Int64
segundo :: Int64
function Hora(hora::Int64=0, minuto::Int64=0, segundo::Int64=0)
@assert(0 ≤ minuto < 60, "Minuto no está entre 0 y 60.")
@assert(0 ≤ segundo < 60, "Segundo no está entre 0 y 60.")
new(hora, minuto, segundo)
end
endLa estructura Hora tiene ahora 4 métodos de constructor interno:
Hora()
Hora(hora::Int64)
Hora(hora::Int64, minuto::Int64)
Hora(hora::Int64, minuto::Int64, segundo::Int64)Un método de constructor interno siempre se define dentro del bloque de una declaración de tipo y tiene acceso a una función especial llamada new que crea objetos del tipo recién declarado.
|
Aviso
|
Si se define algún constructor interno, el constructor por defecto ya no está disponible. Se tienen que escribir explícitamente todos los constructores internos necesarios. |
También existe un método sin argumentos de la función local new:
mutable struct Hora
hora :: Int64
minuto :: Int64
segundo :: Int64
function Hora(hora::Int64=0, minuto::Int64=0, segundo::Int64=0)
@assert(0 ≤ minuto < 60, "Minuto está entre 0 y 60.")
@assert(0 ≤ segundo < 60, "Segundo está entre 0 y 60.")
tiempo = new()
tiempo.hora = hora
tiempo.minuto = minuto
tiempo.segundo = segundo
tiempo
end
endEsto permite construir estructuras de datos recursivas, es decir, una estructura donde uno de los atributos es la estructura misma. En este caso, la estructura debe ser mutable ya que sus atributos se modifican después de la creación de instancias.
show
show es una función especial que devuelve la representación de cadena de un objeto. A continuación se muestra el método show para objetos Hora:
using Printf
function Base.show(io::IO, tiempo::Hora)
@printf(io, "%02d:%02d:%02d", tiempo.hora, tiempo.minuto, tiempo.segundo)
endEsta función guarda como cadena de texto una hora dada en el archivo al que io hace referencia.
El prefijo Base es necesario si se quiere agregar un nuevo método a la función Base.show.
Cuando se imprime un objeto, Julia llama a la función show (esto ocurre siempre, y como agregamos un nuevo método a la función Base.show, entonces se muestra Hora con el formato que queremos):
julia> tiempo = Hora(9, 45, 0)
09:45:00Al escribir un nuevo tipo compuesto, casi siempre es preferible empezar escribiendo un constructor externo, puesto que facilita la creación de instancias de objetos y show, que es útil para la depuración.
Ejercicio 17-2
Escriba un método de constructor externo para la clase Punto que tome x e y como parámetros opcionales y los asigne a los atributos correspondientes.
incrementar (generic function with 1 method)
Sobrecarga de Operadores
Es posible cambiar la definición de los operadores cuando se aplican a tipos definidos por el usuario. Esto se hace definiendo métodos del operador. Por ejemplo, si se define un método llamado + con dos argumentos Hora, se puede usar el operador + en los objetos Hora.
Así es como se vería la definición:
import Base.+
function +(t1::Hora, t2::Hora)
segundos = horaaentero(t1) + horaaentero(t2)
enteroahora(segundos)
endLa sentencia import agrega el operador + al ámbito local (local scope) para que se puedan agregar métodos.
A continuación se muestra cómo usar este operador para objetos Hora:
julia> inicio = Hora(9, 45)
09:45:00
julia> duracion = Hora(1, 35, 0)
01:35:00
julia> inicio + duracion
11:20:00Al aplicar el operador + a objetos Hora, Julia invoca el método recién agregado. Cuando REPL muestra el resultado, Julia invoca a show. ¡Hay muchas cosas ocurriendo pero que no se observan!
Ampliar el comportamiento de los operadores de modo que funcionen con tipos definidos por el usuario/programador se denomina sobrecarga del operador.
Dispatch Múltiple
En la sección anterior se sumaron dos objetos Hora. Imagine que ahora se quiere sumar un número entero a un objeto Hora:
function +(tiempo::Hora, segundos::Int64)
incrementar(tiempo, segundos)
endHe aquí un ejemplo que usa el operador + con un objeto Hora y un entero:
julia> inicio = Hora(9, 45)
09:45:00
julia> inicio + 1337
10:07:17La suma es un operador conmutativo, por lo que se debe agregar otro método.
function +(segundos::Int64, tiempo::Hora)
tiempo + segundos
endY se obtiene el mismo resultado:
julia> 1337 + inicio
10:07:17La elección del método a ejecutar cuando se aplica una función se llama dispatch. Julia permite que el proceso de dispatch elija a cuál de los métodos de una función llamar en función del número y tipo de los argumentos dados. El uso de todos los argumentos de una función para elegir el método que se debe invocar se conoce como dispatch múltiple.
Ejercicio 17-3
Escriba los siguientes métodos + para objetos Punto:
-
Si ambos operandos son objetos Punto, el método debería devolver un nuevo objeto Punto cuya coordenada
xsea la suma de las coordenadasxde los operandos. De manera análoga, haga lo mismo para la coordenaday. -
Si el primer o el segundo operando es una tupla, el método debe agregar el primer elemento de la tupla a la coordenada
xy el segundo elemento a la coordenaday, y devolver un nuevo objeto Punto con el resultado.
Programación Genérica
El dispatch múltiple es útil cuando es necesario, pero (afortunadamente) no siempre lo es. A menudo puede evitarse escribiendo funciones que funcionen correctamente para argumentos de diferentes tipos.
Muchas de las funciones que se han visto para cadenas también funcionan para otros tipos de secuencia. Por ejemplo, en Sección 11.2 se usa histograma para contar la cantidad de veces que cada letra aparece en una palabra.
function histograma(s)
d = Dict()
for c in s
if c ∉ keys(d)
d[c] = 1
else
d[c] += 1
end
end
d
endEsta función también funciona para listas, tuplas e incluso diccionarios, siempre y cuando los elementos de s sean hashables, ya que así pueden usarse como claves de d.
julia> t = ("spam", "huevo", "spam", "spam", "tocino", "spam")
("spam", "huevo", "spam", "spam", "tocino", "spam")
julia> histograma(t)
Dict{Any,Any} with 3 entries:
"spam" => 4
"huevo" => 1
"tocino" => 1Las funciones que pueden tomar parámetros de diferentes tipos se llaman polimórficas. El polimorfismo puede facilitar la reutilización del código.
Por ejemplo, la función integrada sum, que suma los elementos de una secuencia, funciona siempre que los elementos de la secuencia permitan la suma.
Como se añadió el método + para los objetos Hora, entonces se puede usar sum para Hora:
julia> t1 = Hora(1, 7, 2)
01:07:02
julia> t2 = Hora(1, 5, 8)
01:05:08
julia> t3 = Hora(1, 5, 0)
01:05:00
julia> sum((t1, t2, t3))
03:17:10Si todas las operaciones realizadas dentro de la función se pueden aplicar al tipo, la función se puede aplicar al tipo.
El mejor tipo de polimorfismo es el que no se busca: cuando usted descubre que una función que había escrito se puede aplicar a un tipo para el que nunca la había planeado.
Interfaz e implementación
Uno de los objetivos del dispatch múltiple es hacer que el software sea más fácil de mantener, lo que significa poder mantener el programa funcionando cuando otras partes del sistema cambian y modificar el programa para cumplir con los nuevos requisitos.
Una técnica de diseño que ayuda a lograr ese objetivo es mantener las interfaces separadas de las implementaciones. Esto significa que los métodos que tienen un argumento con anotación de tipo no deberían depender de cómo se representan los atributos de ese tipo.
Por ejemplo, en este capítulo se desarrolla una estructura que representa una hora del día. Los métodos que tienen un argumento con anotación de este tipo incluyen horaaentero, estadespues y +.
Se pueden implementar esos métodos de varias maneras. Los detalles de la implementación dependen de cómo se represente Hora. En este capítulo, los atributos de un objeto Hora son hora, minuto y segundo.
Otra opción sería reemplazar estos atributos con un solo entero que represente el número de segundos desde la medianoche. Esta implementación haría que algunas funciones, como estadespues, sean más fáciles de escribir, pero hace que otras sean más difíciles.
Después de implementar un tipo, puede descubrir una mejor implementación. Si otras partes del programa están usando su tipo, cambiar la interfaz puede llevar mucho tiempo y ser propenso a errores. No obstante, si hizo un buen diseñó de interfaz, puede cambiar la implementación sin cambiar la interfaz, lo que significa que otras partes del programa no tienen que cambiar.
Depuración
Llamar a una función con los argumentos correctos puede ser difícil cuando se especifica más de un método para la función. Julia permite examinar las especificaciones de los métodos de una función.
Para saber qué métodos están disponibles para una función determinada, puede usar la función methods:
julia> methods(imprimirhora)
# 2 methods for generic function "imprimirhora":
[1] printtime(time::MyTime) in Main at REPL[3]:2
[2] printtime(time) in Main at REPL[4]:2En este ejemplo, la función imprimirhora tiene 2 métodos: uno con un argumento Hora y otro con un argumento Any.
Glosario
- anotación de tipo
-
El operador
::seguido de un tipo que indica que una expresión o una variable es de ese tipo. - método
-
Una definición de un posible comportamiento de una función.
- dispatch
-
La elección de qué método ejecutar cuando se ejecuta una función.
- especificación
-
El número y tipo de argumentos de un método que permite al dispatch seleccionar el método más específico de una función durante la llamada a función.
- constructor externo
-
Constructor definido fuera de la definición de tipo para definir métodos útiles para crear un objeto.
- constructor interno
-
Constructor definido dentro de la definición de tipo para imponer invariantes o para construir objetos recursivos.
- constructor por defecto
-
Constructor interno que está disponible cuando el usuario no define constructores internos.
- constructor de copia
-
Método de constructor externo de un tipo, que tiene como único argumento un objeto del tipo. Crea un nuevo objeto que es una copia del argumento.
- sobrecarga de operadores
-
Ampliar el comportamiento de los operadores como ++ de modo que trabajen con tipos definidos por el usuario.
- dispatch múltiple
-
Dispatch basado en todos los argumentos de una función.
- programación genérica
-
Escribir código que pueda funcionar con más de un tipo.
Ejercicios
Ejercicio 17-4
Cambie los atributos de Hora para que sea un solo número entero que represente los segundos desde la medianoche. Luego modifique los métodos definidos en este capítulo para que funcionen con la nueva implementación.
Ejercicio 17-5
Escriba una definición para un tipo llamado Canguro, con un atributo llamado contenidodemarsupio de tipo Arreglo y los siguientes métodos:
-
Un constructor que inicialice
contenidodemarsupioa un arreglo vacío. -
Un método llamado
ponerenmarsupioque tome un objetoCanguroy un objeto de cualquier tipo y lo agregue acontenidodemarsupio. -
Un método
showque devuelva una representación de cadena del objetoCanguroy el contenido del marsupio.
Pruebe su código creando dos objetos Canguro, asignándolos a variables llamadas cangu y ro, y luego agregando ro al contenido del marsupio de cangu.
18. Subtipos
En el capítulo anterior se presentó el dispatch múltiple y los métodos polimórficos. Al no especificar el tipo de los argumentos de un método, este se puede invocar con argumentos de cualquier tipo. Ahora se verá cómo especificar un subconjunto de tipos permitidos en las especificaciones de un método.
En este capítulo se explica el concepto de subtipo usando tipos que representan naipes, mazos de naipes y manos de póker.
Si usted nunca ha jugado póker, puede leer sobre él en https://es.wikipedia.org/wiki/P%C3%B3quer, aunque no es necesario ya que se explicará todo lo necesario para los ejercicios.
Naipes
Hay cincuenta y dos naipes en una baraja inglesa, cada uno de los cuales pertenece a uno de los cuatro palos y tiene un valor. Los palos son Picas (♠), Corazones (♥), Diamantes (♦) y Tréboles (♣). Los valores son As (A), 2, 3, 4, 5, 6, 7, 8, 9, 10, Jota (J), Reina (Q) y Rey (K). Dependiendo del tipo de juego, el valor del As puede ser mayor que al Rey o inferior al 2.
Si queremos definir un nuevo objeto para representar un naipe, son obvios los atributos que debería tener: valor y palo. Lo que no es tan obvio es el tipo que se debe dar a estos atributos. Una opción es usar cadenas de caracteres que contengan palabras como "Picas" para los palos y "Reina" para los valores. Un problema de esta implementación es que no sería fácil comparar naipes para ver cuál tiene mayor valor o palo.
Una alternativa es usar números enteros para codificar los valores y palos. En este contexto, "codificar" significa definir una asociación entre números y palos, o entre números y valores. Este tipo de codificación no está relacionada con cifrar o traducir a un código secreto (eso sería "cifrado").
Por ejemplo, esta tabla muestra una correspondencia entre palos y códigos (números) enteros:
-
♠\(\mapsto\) 4 -
♥\(\mapsto\) 3 -
♦\(\mapsto\) 2 -
♣\(\mapsto\) 1
Este código facilita la comparación de naipes; los palos más altos se asignan a los números más altos, por lo tanto podemos comparar los palos al comparar sus códigos.
Estamos usando el símbolo \(\mapsto\) para dejar en claro que estas asignaciones no son parte de Julia. Forman parte del diseño del programa, pero no aparecen explícitamente en el código.
La definición de estructura de Naipe se ve así:
struct Naipe
palo :: Int64
valor :: Int64
function Naipe(palo::Int64, valor::Int64)
@assert(1 ≤ palo ≤ 4, "el palo no está entre 1 y 4")
@assert(1 ≤ valor ≤ 13, "el valor no está entre 1 y 13")
new(palo, valor)
end
endPara crear un Naipe, se debe llamar a Naipe con el palo y el valor del naipe deseado:
julia> reina_de_diamantes = Naipe(2, 12)
Naipe(2, 12)Variables Globales
Para poder imprimir los objetos Naipe de una manera que sea fácil de leer, se necesita establecer una correspondencia entre los códigos enteros y sus correspondientes palos y valores. Una manera natural de hacer esto es con arreglos de cadenas:
const nombres_palo = ["♣", "♦", "♥", "♠"]
const nombres_valor = ["A", "2", "3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K"]Las variables nombres_palo y nombres_valor son variables globales. La declaración const significa que la variable solo se puede asignar una vez. Esto resuelve el problema de rendimiento de las variables globales.
Ahora se puede implementar un método show apropiado:
function Base.show(io::IO, naipe::Naipe)
print(io, nombres_valor[naipe.valor], nombres_palo[naipe.palo])
endLa expresión nombres_valor[naipe.valor] significa "use el atributo valor del objeto naipe como índice en el arreglo nombres_valor, y seleccione la cadena correspondiente".
Con los métodos que se tienen hasta ahora, se pueden crear e imprimir naipes:
julia> Naipe(3, 11)
J♥Comparación de naipes
Para los tipos integrados, existen operadores relacionales (<, >, ==, etc.) que comparan valores y determinan cuándo uno es mayor, menor o igual a otro. Para los tipos definidos por el usuario, se puede sustituir el comportamiento de estos operadores si se proporciona un método llamado: <.
El orden correcto de los naipes no es obvio. Por ejemplo, ¿cuál es mejor, el 3 de Tréboles o el 2 de Diamantes? Uno tiene un valor mayor, pero el otro tiene un palo mayor. Para hacer que los naipes sean comparables, se debe decidir qué es más importante: valor o palo.
La respuesta puede depender del tipo de juego, pero para simplificar las cosas, se establece la elección arbitraria de que el palo es más importante, por lo que todas los tréboles superan a todos los diamantes, y así sucesivamente.
Con esa decisión tomada, se puede escribir <:
import Base.<
function <(c1::Naipe, c2::Naipe)
(c1.palo, c1.valor) < (c2.palo, c2.valor)
endEjercicio 18-1
Escriba un método < para objetos Hora. Puede usar comparación de tuplas, o comparación de enteros.
Prueba unitaria
Una prueba unitaria permite verificar el correcto funcionamiento de su código comparando los resultados obtenidos con los esperados. Esto puede ser útil para verificar que su código funciona correctamente después de haberlo modificado, y también es una forma de predefinir el comportamiento correcto de su código durante el desarrollo.
Se pueden realizar pruebas unitarias simples con las macros @test:
julia> using Test
julia> @test Naipe(1, 4) < Naipe(2, 4)
Test Passed
julia> @test Naipe(1, 3) < Naipe(1, 4)
Test Passed@test devuelve "Test Passed" ("Prueba aprobada") si la expresión que sigue es true, "Test Failed" ("Prueba fallida") si es false, y "Error Result" ("Resultado de error") si no se pudo evaluar.
Mazos
Ahora que ya tenemos Naipes, el próximo paso es definir Mazos. Como un mazo está compuesto de naipes, naturalmente cada Mazo contendrá un arreglo de naipes como atributo.
A continuación se muestra una definición para Mazo. El constructor crea el atributo naipes y genera la baraja estándar de cincuenta y dos naipes:
struct Mazo
naipes :: Array{Naipe, 1}
end
function Mazo()
mazo = Mazo(Naipe[])
for palo in 1:4
for valor in 1:13
push!(mazo.naipes, Naipe(palo, valor))
end
end
mazo
endLa forma más fácil de poblar el mazo es mediante un bucle anidado. El bucle exterior enumera los palos desde 1 hasta 4. El bucle interior enumera los valores desde 1 hasta 13. Cada iteración crea un nuevo Naipe con el palo y valor actual, y lo agrega a mazo.naipes.
Este es un método show para Mazo:
function Base.show(io::IO, mazo::Mazo)
for naipe in mazo.naipes
print(io, naipe, " ")
end
println()
endAsí es como se ve el resultado:
julia> Mazo()
A♣ 2♣ 3♣ 4♣ 5♣ 6♣ 7♣ 8♣ 9♣ 10♣ J♣ Q♣ K♣ A♦ 2♦ 3♦ 4♦ 5♦ 6♦ 7♦ 8♦ 9♦ 10♦ J♦ Q♦ K♦ A♥ 2♥ 3♥ 4♥ 5♥ 6♥ 7♥ 8♥ 9♥ 10♥ J♥ Q♥ K♥ A♠ 2♠ 3♠ 4♠ 5♠ 6♠ 7♠ 8♠ 9♠ 10♠ J♠ Q♠ K♠Añadir, Eliminar, Barajar y Ordenar
Para repartir los naipes, se debe tener una función que elimine un naipe del mazo y lo devuelva. La función pop! proporciona una forma conveniente de realizar esto:
function Base.pop!(mazo::Mazo)
pop!(mazo.naipes)
endComo pop! elimina el último naipe en el arreglo, se está repartiendo desde el extremo inferior del mazo.
Para añadir un naipe, se puede usar la función push!:
function Base.push!(mazo::Mazo, naipe::Naipe)
push!(mazo.naipes, naipe)
mazo
endUn método como este, que usa otro método sin hacer mucho más, se llama enchapado. La metáfora proviene de la carpintería, donde un enchapado es una capa fina de madera de alta calidad que se pega a la superficie de una pieza de madera de baja calidad para mejorar su apariencia.
En este caso, push! es un método "fino" que expresa una operación de arreglos adecuada para los mazos. Mejora la apariencia o interfaz, de la implementación.
También podemos escribir un método llamado shuffle! (barajar en inglés) usando la función Random.shuffle!:
using Random
function Random.shuffle!(mazo::Mazo)
shuffle!(mazo.naipes)
mazo
endEjercicio 18-2
Escriba una función llamada sort! (ordenar en inglés) que use la función sort! para ordenar las cartas en un Mazo. sort! usa el método isless que definimos para determinar el orden.
Tipos Abstractos y Subtipos
Se busca que un tipo represente una "mano", es decir, los naipes que tiene un jugador. Una mano es similar a un mazo: ambos están compuestos de un conjunto de naipes y ambos requieren de operaciones tales como agregar y eliminar una carta.
Una mano es diferente de un mazo en ciertos aspectos ya que existen ciertas operaciones sobre una mano que no tendrían sentido sobre un mazo. Por ejemplo, en el poker se debe comparar una mano con otra para ver quién gana. En bridge, se necesita calcular el puntaje de la mano para así poder hacer la subasta.
Por lo tanto, hace falta una forma de agrupar los tipos concretos que están relacionados. En Julia, esto se hace definiendo un abstract type (tipo abstracto en inglés) que sea padre de Mazo y Mano. A esto se le llama crear subtipos.
Se llama al tipo abstracto ConjuntoDeCartas:
abstract type ConjuntoDeCartas endSe puede crear un nuevo tipo abstracto con la palabra reservada abstract type. De manera opcional, se puede especificar un tipo "padre" de una estructura colocando después del nombre de esta, el símbolo <: seguido del nombre de un tipo abstracto existente.
Cuando no se proporciona un supertipo, el supertipo por defecto es Any, es decir, un tipo abstracto predefinido del que todos los objetos son instancias y del que todos los tipos son subtipos.
Ahora se puede expresar que Mazo es un "hijo" de ConjuntoDeCartas:
struct Mazo <: ConjuntoDeCartas
naipes :: Array{Naipe, 1}
end
function Mazo()
mazo = Mazo(Naipe[])
for palo in 1:4
for valor in 1:13
push!(mazo.naipes, Naipe(palo, valor))
end
end
mazo
endEl operador isa comprueba si un objeto es de un tipo dado:
julia> mazo = Mazo();
julia> mazo isa ConjuntoDeCartas
trueUna mano también es un ConjuntoDeCartas:
struct Mano <: ConjuntoDeCartas
naipes :: Array{Naipe, 1}
etiqueta :: String
end
function Mano(etiqueta::String="")
Mano(Naipe[], etiqueta)
endEn lugar de llenar la mano con 52 naipes nuevos, el constructor de Mano inicializa naipes a un arreglo vacío. Se puede etiquetar a la Mano pasando un argumento opcional al constructor.
julia> mano = Mano("nueva mano")
Mano(Naipe[], "nueva mano")Tipos Abstractos y Funciones
Ahora podemos expresar las operaciones que tienen en común Mazo y Mano, al ser funciones que tienen como argumento a ConjuntoDeCartas:
function Base.show(io::IO, cdc::ConjuntoDeCartas)
for naipe in cdc.naipes
print(io, naipe, " ")
end
end
function Base.pop!(cdc::ConjuntoDeCartas)
pop!(cdc.naipes)
end
function Base.push!(cdc::ConjuntoDeCartas, naipe::Naipe)
push!(cdc.naipes, naipe)
nothing
endSe puede usar pop! y push! para repartir una carta:
julia> mazo = Mazo()
A♣ 2♣ 3♣ 4♣ 5♣ 6♣ 7♣ 8♣ 9♣ 10♣ J♣ Q♣ K♣ A♦ 2♦ 3♦ 4♦ 5♦ 6♦ 7♦ 8♦ 9♦ 10♦ J♦ Q♦ K♦ A♥ 2♥ 3♥ 4♥ 5♥ 6♥ 7♥ 8♥ 9♥ 10♥ J♥ Q♥ K♥ A♠ 2♠ 3♠ 4♠ 5♠ 6♠ 7♠ 8♠ 9♠ 10♠ J♠ Q♠ K♠
julia> shuffle!(mazo)
10♣ 9♥ 7♠ 2♠ A♥ 4♣ J♥ 2♦ 6♣ Q♣ 8♦ 8♥ 3♥ 7♣ 3♦ 2♣ J♣ 8♣ 9♦ 6♠ 3♠ 5♠ A♦ A♣ 10♥ 4♠ Q♥ J♦ K♠ 10♦ K♥ K♣ 5♣ 5♥ 5♦ 10♠ 7♦ 3♣ 9♠ A♠ 2♥ 7♥ 9♣ Q♦ 6♥ 8♠ J♠ 4♦ Q♠ 6♦ K♦ 4♥
julia> naipe = pop!(mazo)
4♥
julia> push!(mano, naipe)A continuación, se encapsula este código en una función llamada mover!:
function mover!(cdc1::ConjuntoDeCartas, cdc2::ConjuntoDeCartas, n::Int)
@assert 1 ≤ n ≤ length(cs1.naipes)
for i in 1:n
naipe = pop!(cdc1)
push!(cdc2, naipe)
end
nothing
endmover! toma tres argumentos: dos objetos ConjuntoDeCartas y el número de cartas a repartir. Modifica ambos objetos ConjuntoDeCartas, y devuelve nothing.
En algunos juegos, las cartas se mueven de una mano a otra, o de una mano al mazo. Puede usar mover! para cualquiera de estas operaciones: cdc1 y cdc2 pueden ser un Mazo o una Mano.
Diagramas de tipos
Hasta ahora se han visto diagramas de pila, que muestran el estado de un programa, y diagramas de objetos, que muestran los atributos de un objeto y sus valores. Estos diagramas son como una foto sacada durante la ejecución de un programa, por lo que cambian a medida que se ejecuta el programa.
También son muy detallados; en algunos casos demasiado detallados. Un diagrama de tipos es una representación más abstracta de la estructura de un programa. En vez de mostrar objetos individuales, muestra los tipos y las relaciones entre ellos.
Hay varias formas de relación entre tipos:
-
Los objetos de un tipo concreto pueden contener referencias a objetos de otro tipo. Por ejemplo, cada Rectángulo contiene una referencia a un Punto, y cada Mazo contiene referencias a un conjunto de Naipes. Este tipo de relación se llama TIENE-UN, como por ejemplo "un Rectángulo tiene un Punto".
-
Un tipo concreto puede tener un tipo abstracto como supertipo. Esta relación se llama ES-UN, como por ejemplo "una Mano es un ConjuntoDeCartas".
-
Un tipo puede depender de otro si los objetos de un tipo toman objetos del segundo tipo como parámetros o usan objetos del segundo tipo como parte de un cálculo. Este tipo de relación se llama dependencia.
Cada una de las flechas superiores representa una relación ES-UN. En este caso, indica que Mano tiene como supertipo a ConjuntoDeCartas.
Cada una de las flechas inferiores representa una relación TIENE-UN; en este caso, un Mazo tiene referencias a objetos Naipe.
El asterisco (*) cerca de la flecha es una multiplicidad e indica cuántos Naipes tiene un Mazo. Una multiplicidad puede ser un número simple, como 52; un rango, como 5:7 o un asterisco, lo cual indica que un Mazo puede tener cualquier número de Naipes.
No hay dependencias en este diagrama. Normalmente se mostrarían con una flecha achurada. Si hay muchas dependencias, a veces se omiten.
Un diagrama más detallado podría mostrar que un Mazo en realidad contiene un arreglo de Naipes, pero los tipos integrados como arreglos y diccionarios generalmente no se incluyen en los diagramas de tipos.
Depuración
Utilizar subtipos puede dificultar la depuración ya que al llamar a una función con un objeto como argumento, puede ser complicado determinar qué método se invocará.
Al escribir una función que funciona con objetos Mano, se busca que funcione con todo tipo de Manos, como ManoDePoker, ManoDeBridge, etc. Si el usuario invoca un método como sort!, podría obtener el método definido para un tipo abstracto Mano, pero si existiera un método sort! que tuviera como argumento cualquiera de estos subtipos de Mano, obtendría esa versión. Este comportamiento suele ser algo bueno, pero puede ser confuso.
function Base.sort!(mano::Mano)
sort!(mano.naipes)
endSi usted no está seguro del flujo de ejecución de un programa, la solución más simple es agregar sentencias de impresión al inicio de sus métodos más relevantes. Si shuffle! imprimiera un mensaje como Ejecutando shuffle! en Mazo durante la ejecución del programa, sería posible rastrear el flujo de ejecución.
Una mejor alternativa es la macro @which:
julia> @which sort!(mano)
sort!(mano::Mano) in Main at REPL[5]:1Entonces, el método sort! de mano es el que tiene como argumento un objeto de tipo Mano.
Una sugerencia para el diseño del programa: cuando anula un método, la interfaz del nuevo método debería ser la misma que la anterior. Debería tomar los mismos parámetros, devolver el mismo tipo y obedecer las mismas condiciones previas y posteriores. Si sigue esta regla, cualquier función diseñada para funcionar con una instancia de un supertipo, como un ConjuntoDeCartas, también funcionará con instancias de sus subtipos Mazo y Mano.
Si viola esta regla, llamada "principio de sustitución de Liskov", su código colapsará como un castillo de naipes (jeje).
La función supertype permite encontrar el supertipo directo de un tipo.
julia> supertype(Mazo)
ConjuntoDeCartasEncapsulado de Datos
Los capítulos anteriores muestran un plan de desarrollo que podríamos llamar "diseño orientado a tipos". Se identifican los objetos necesarios, como Punto, Rectángulo y Hora, y se definen estructuras para representarlos. En cada caso hay una correspondencia obvia entre el objeto y alguna entidad en el mundo real (o al menos en el mundo matemático).
A veces no es tan obvio saber qué objetos se necesitan y cómo estos deben interactuar. En ese caso, se necesita un plan de desarrollo diferente. Lo mismo que ocurre con interfaces de funciones por encapsulado y generalización ocurre con interfaces de tipo por encapsulado de datos.
El análisis de Markov, de Sección 13.8, es un buen ejemplo. Si descarga el código desde https://github.com/BenLauwens/ThinkJulia.jl/blob/master/src/solutions/chap13.jl, verá que se usan dos variables globales: sufijos y prefijo, las cuales se leen y escriben desde varias funciones.
sufijos = Dict()
prefijos = []Debido a que estas variables son globales, solo se puede ejecutar un análisis a la vez. Si se leen dos textos, sus prefijos y sufijos se agregarían a las mismas estructuras de datos (lo que generaría un texto interesante).
Para ejecutar múltiples análisis y mantenerlos separados, se puede encapsular el estado de cada análisis en un objeto. Así es como se vería:
struct Markov
orden :: Int64
sufijos :: Dict{Tuple{String,Vararg{String}}, Array{String, 1}}
prefijo :: Array{String, 1}
end
function Markov(orden::Int64=2)
new(orden, Dict{Tuple{String,Vararg{String}}, Array{String, 1}}(), Array{String, 1}())
endA continuación, se transforman las funciones en métodos. Por ejemplo, para procesarpalabra:
function procesarpalabra(markov::Markov, palabra::String)
if length(markov.prefijo) < markov.orden
push!(markov.prefijo, palabra)
return
end
get!(markov.sufijos, (markov.prefijo...,), Array{String, 1}())
push!(markov.sufijos[(markov.prefijo...,)], palabra)
popfirst!(markov.prefijo)
push!(markov.prefijo, palabra)
endTransformar un programa así (cambiando el diseño sin cambiar el comportamiento) es otro ejemplo de refactorización (vea Sección 4.7).
Este ejemplo sugiere el siguiente plan de desarrollo para diseñar tipos:
-
Comience escribiendo funciones que lean y escriban variables globales (cuando sea necesario).
-
Una vez que el programa esté funcionando, busque asociaciones entre las variables globales y las funciones que las usan.
-
Encapsule variables relacionadas como atributos de una estructura.
-
Transforme las funciones asociadas en métodos que tengan como argumentos objetos del nuevo tipo.
Exercise 18-3
Descargue el código de Markov de https://github.com/BenLauwens/ThinkJulia.jl/blob/master/src/solutions/chap13.jl y siga los pasos descritos anteriormente para encapsular las variables globales como atributos de una nueva estructura llamada Markov.
Glosario
- codificar
-
Representar un conjunto de valores utilizando otro conjunto de valores, generando una asociación entre ellos.
- prueba unitaria
-
Manera estandarizada de probar que el código está correcto.
- enchapado
-
Un método o función que mejora la interfaz de otra función sin hacer muchos cálculos.
- crear subtipos
-
La capacidad de definir una jerarquía de tipos relacionados.
- tipo abstracto
-
Un tipo que puede ser padre de otro tipo.
- tipo concreto
-
Un tipo que se puede construir.
- subtipo
-
Un tipo que tiene como padre un tipo abstracto.
- supertipo
-
Un tipo abstracto que es el padre de otro tipo.
- relación ES-UN
-
Una relación entre un subtipo y su supertipo.
- relación TIENE-UN
-
Una relación entre dos tipos donde las instancias de un tipo contienen referencias a instancias del otro.
- dependencia
-
Una relación entre dos tipos donde las instancias de un tipo usan instancias del otro tipo, pero no las almacenan como atributos.
- diagrama de tipos
-
Un diagrama que muestra los tipos en un programa y las relaciones entre ellos.
- multiplicidad
-
Una notación en un diagrama de tipo que muestra, para una relación TIENE-UN, cuántas referencias hay a instancias de otra clase.
- encapsulado de datos
-
Un plan de desarrollo de programas que implica hacer un prototipo que use variables globales y una versión final que convierta las variables globales en atributos de instancia.
Ejercicios
Ejercicio 18-4
Para el siguiente programa, dibuje un diagrama de tipos que muestre estos tipos y las relaciones entre ellos.
abstract type PadrePingPong end
struct Ping <: PadrePingPong
pong :: PadrePingPong
end
struct Pong <: PadrePingPong
pings :: Array{Ping, 1}
function Pong(pings=Array{Ping, 1}())
new(pings)
end
end
function agregarping(pong::Pong, ping::Ping)
push!(pong.pings, ping)
nothing
end
pong = Pong()
ping = Ping(pong)
agregarping(pong, ping)Ejercicio 18-5
Escriba un método llamado repartir! que tome tres parámetros: un Mazo, el número de manos y el número de naipes por mano. Debería crear el número apropiado de objetos Mano, repartir el número apropiado de naipes por mano y devolver un arreglo de Manos.
Ejercicio 18-6
Las siguientes son las posibles manos en el póker, en orden de valor creciente y probabilidad decreciente:
- pareja
-
Dos cartas del mismo número.
- doble pareja
-
Dos pares de cartas del mismo número.
- trío
-
Tres cartas del mismo número.
- escalera
-
Cinco cartas consecutivas (los ases pueden ser considerados altos o bajos, por lo tanto As-2-3-4-5 es escalera, 10-Jota-Reina-Rey-As también, pero Reina-Rey-As-2-3 no).
- color
-
Cinco cartas del mismo palo.
- full
-
Tres cartas iguales en su valor, más otras dos iguales en su valor.
- póker
-
Cuatro cartas iguales en su valor.
- escalera de color
-
Cinco cartas consecutivas del mismo palo.
El objetivo de este ejercicio es estimar la probabilidad de tener cada una de estas manos.
-
Agregue métodos llamados
tienepareja,tienedoblepareja, etc. que devuelvantrueofalsesegún si la mano cumple o no con los criterios relevantes. Su código debería funcionar correctamente para manos que contengan cualquier número de naipes (aunque 5 y 7 son los tamaños más comunes). -
Escriba un método llamado
clasificarque descubra la clasificación de mayor valor para una mano, y defina el atributoetiquetacon esta clasificación. Por ejemplo, una mano de 7 cartas que contiene un color y una pareja, debe etiquetarse como "color". -
Cuando esté convencido de que sus métodos de clasificación están funcionando correctamente, estime las probabilidades de las distintas manos. Escriba una función que baraje un mazo de naipes, la divida en diferentes manos, clasifique las manos y cuente la cantidad de veces que aparecen varias clasificaciones.
-
Imprima una tabla de las clasificaciones y sus probabilidades. Ejecute su programa con un número cada vez mayor de manos hasta que los valores de salida converjan con un grado razonable de precisión. Compare sus resultados con los valores en https://en.wikipedia.org/wiki/Hand_rankings.
19. Extra: Sintaxis
Uno de los objetivos de este libro es enseñarle lo justo y necesario de Julia. Se explica una sola forma de hacer las cosas y, en ocasiones, se deja como ejercicio al lector una segunda manera.
Ahora se verán algunos temas que se han dejado de lado pero que son útiles. Julia proporciona una serie de características que no son realmente necesarias (se puede escribir un buen código sin ellas), pero a veces permiten escribir un código más conciso, legible y/o eficiente.
En este capítulo y el siguiente se discute aquello que se ha omitido en los capítulos anteriores:
-
más sintaxis
-
funciones, tipos y macros disponibles directamente de
Base -
funciones, tipos y macros de la Biblioteca Estándar (Standard Library)
Tuplas con nombre
Es posible colocarle nombre a los componentes de una tupla, creando una tupla con nombre:
julia> x = (a=1, b=1+1)
(a = 1, b = 2)
julia> x.a
1En las tuplas con nombre se puede acceder a los atributos con su nombre utilizando la sintaxis de punto (x.a).
Funciones
Las funciones en Julia también se pueden definir mediante una sintaxis compacta, de la siguiente forma:
julia> f(x,y) = x + y
f (generic function with 1 method)Funciones Anonimas
Podemos definir una función sin especificar su nombre:
julia> x -> x^2 + 2x - 1
#1 (generic function with 1 method)
julia> function (x)
x^2 + 2x - 1
end
#3 (generic function with 1 method)Estos son ejemplos de funciones anónimas. Las funciones anónimas generalmente se usan como argumento de otra función:
julia> using Plots
julia> plot(x -> x^2 + 2x - 1, 0, 10, xlabel="x", ylabel="y")Figura 24 muestra el resultado del comando plot (graficar en inglés).
Argumentos con nombre
También se puede poner nombre a los argumentos de una función:
julia> function migrafico(x, y; style="continua", width=1, color="negro")
###
end
migrafico (generic function with 1 method)
julia> migrafico(0:10, 0:10, style="dotted", color="blue")Los argumentos con nombre en una función se especifican después de un punto y coma en la especificación, pero al llamar a la función se pueden utilizar solo comas.
Clausuras
Una clausura es una técnica que permite que una función capture una variable definida fuera del ámbito de la función.
julia> foo(x) = ()->x
foo (generic function with 1 method)
julia> bar = foo(1)
#1 (generic function with 1 method)
julia> bar()
1En este ejemplo, la función foo devuelve una función anónima que tiene acceso al argumento x de la función foo. bar apunta a la función anónima y devuelve el valor del argumento de foo.
Bloques
Un bloque es una forma de agrupar varias sentencias. Un bloque comienza con la palabra reservada begin y termina con end.
En Capítulo 4 se presentó la macro @svg:
🐢 = Turtle()
@svg begin
forward(🐢, 100)
turn(🐢, -90)
forward(🐢, 100)
endEn este ejemplo, la macro @svg tiene un único argumento: un bloque, que agrupa 3 llamadas a funciones.
Bloques let
Un bloque let es útil para crear nuevas ligaduras (o bindings), es decir, variables locales que pueden apuntar a valores.
julia> x, y, z = -1, -1, -1;
julia> let x = 1, z
@show x y z;
end
x = 1
y = -1
ERROR: UndefVarError: z not defined
julia> @show x y z;
x = -1
y = -1
z = -1En el ejemplo, la primera macro @show muestra la variable local x, la variable global y y la variable local indefinida z. Las variables globales se mantienen intactas.
Bloques do
En Sección 14.2 se cierra el archivo después de terminar de escribir en él. Esto se puede hacer automáticamente usando un Bloque do:
julia> datos = "El Cid convoca a sus vasallos;\néstos se destierran con él.\n"
"El Cid convoca a sus vasallos;\néstos se destierran con él.\n"
julia> open("salida.txt", "w") do fout
write(fout, datos)
end
61En este ejemplo, fout es el archivo stream utilizado para la salida.
Esto es equivalente a:
julia> f = fout -> begin
write(fout, datos)
end
#3 (generic function with 1 method)
julia> open(f, "salida.txt", "w")
61La función anónima se utiliza como primer argumento de la función open:
function open(f::Function, args...)
io = open(args...)
try
f(io)
finally
close(io)
end
endUn bloque do puede "capturar" variables de su ámbito envolvente (enclosed scope). Por ejemplo, la variable datos en el ejemplo anterior de open ... do es capturada desde el ámbito externo.
Estructuras de control
Operador ternario
El operador ternario, ?:, puede utilizarse en vez de una sentencia if-elseif. Esta sentencia se usa cuando se necesita elegir entre diferentes expresiones con valor único.
julia> a = 150
150
julia> a % 2 == 0 ? println("par") : println("impar")
parLa expresión que va antes de ? es una expresión de condición. Si la condición es true, se evalúa la expresión que va antes de :. De lo contrario, se evalúa la expresión que va después de :.
Evaluación de cortocircuito
Los operadores && y || realizan una evaluación de cortocircuito, es decir, se evalúa el siguiente argumento solo cuando es necesario para determinar el valor final.
Por ejemplo, una función factorial recursiva podría definirse así:
function fact(n::Integer)
n >= 0 || error("n debe ser no negativo")
n == 0 && return 1
n * fact(n-1)
endTarea (o Corrutina)
Una tarea es una estructura de control que puede ceder el control de forma cooperativa sin hacer return. En Julia, una tarea puede implementarse como una función con un objeto Channel como primer argumento. Se usa un channel para pasar valores de la función a la sentencia que la llama.
El término "cooperativo" alude a que los programas deben cooperar para que todo el esquema de programación funcione.
La secuencia de Fibonnaci se puede generar mediante una tarea.
function fib(c::Channel)
a = 0
b = 1
put!(c, a)
while true
put!(c, b)
(a, b) = (b, a+b)
end
endput! almacena valores en un objeto channel y take! lee valores desde él:
julia> fib_gen = Channel(fib);
julia> take!(fib_gen)
0
julia> take!(fib_gen)
1
julia> take!(fib_gen)
1
julia> take!(fib_gen)
2
julia> take!(fib_gen)
3El constructor Channel crea la tarea. La función fib se suspende después de cada llamada a put! y se reanuda al llamar a take!. Por razones de rendimiento, se almacenan varios valores de la secuencia en el objeto channel durante un ciclo de reanudación/suspensión.
Un objeto channel también se puede usar como iterador:
julia> for val in Channel(fib)
print(val, " ")
val > 20 && break
end
0 1 1 2 3 5 8 13 21Tipos
Tipos Primitivos
Un tipo concreto compuesto por bits se llama tipo primitivo. A diferencia de la mayoría de los lenguajes, en Julia se puede declarar nuestros propios tipos primitivos. Los tipos primitivos estándar se definen de la misma manera:
primitive type Float64 <: AbstractFloat 64 end
primitive type Bool <: Integer 8 end
primitive type Char <: AbstractChar 32 end
primitive type Int64 <: Signed 64 endEl número en las sentencias especifica cuántos bits son necesarios.
El siguiente ejemplo crea un tipo primitivo Byte y un constructor:
julia> primitive type Byte 8 end
julia> Byte(val::UInt8) = reinterpret(Byte, val)
Byte
julia> b = Byte(0x01)
Byte(0x01)La función reinterpret se usa para almacenar los bits de un entero sin signo con 8 bits (UInt8) en el byte.
Tipos Paramétricos
El sistema de tipos de Julia es paramétrico, lo que significa que los tipos pueden tener parámetros.
Los parámetros de un tipo se colocan después del nombre del tipo, entre llaves:
struct Punto{T<:Real}
x::T
y::T
endCon esto se define un nuevo tipo paramétrico, Punto{T<:Real}, que contiene dos "coordenadas" de tipo T, que puede ser cualquier tipo que tenga Real como supertipo.
julia> Punto(0.0, 0.0)
Punto{Float64}(0.0, 0.0)Además de los tipos compuestos, los tipos abstractos y los tipos primitivos también pueden tener parámetros.
|
Observación
|
Para mejorar el rendimiento, es totalmente recomendable tener tipos concretos como atributos de una estructura, por lo que esta es una buena manera de hacer que |
Union de Tipo
Una union de tipo es un tipo paramétrico abstracto que puede actuar como cualquiera de los tipos de sus argumentos:
julia> EnteroOCadena = Union{Int64, String}
Union{Int64, String}
julia> 150 :: EnteroOCadena
150
julia> "Julia" :: EnteroOCadena
"Julia"Una unión de tipos es, en la mayoría de los lenguajes informáticos, una construcción interna para trabajar con tipos. Sin embargo, Julia pone a disposición esta característica para sus usuarios, ya que permite generar un código eficiente (cuando la unión es entre pocos tipos). Esta característica otorga una gran flexibilidad para controlar el dispatch.
Métodos
Métodos Paramétricos
Las definiciones de métodos también pueden tener parámetros de tipo que limiten su especificación:
julia> espuntoentero(p::Punto{T}) where {T} = (T === Int64)
espuntoentero (generic function with 1 method)
julia> p = Punto(1, 2)
Punto{Int64}(1, 2)
julia> espuntoentero(p)
trueObjetos Similares a Funciones
Cualquier objeto arbitrario de Julia puede hacerse "invocable". Tales objetos "invocables" a veces se denominan funtores.
struct Polinomio{R}
coef::Vector{R}
end
function (p::Polinomio)(x)
val = p.coef[end]
for coef in p.coef[end-1:-1:1]
val = val * x + coef
end
val
endPara evaluar el polinomio, simplemente debemos llamarlo:
julia> p = Polinomio([1,10,100])
Polinomio{Int64}([1, 10, 100])
julia> p(3)
931Constructores
Los tipos paramétricos se pueden construir explícita o implícitamente:
julia> Punto(1,2) # T implicito
Punto{Int64}(1, 2)
julia> Punto{Int64}(1, 2) # T explicito
Punto{Int64}(1, 2)
julia> Punto(1,2.5) # T implicito
ERROR: MethodError: no method matching Punto(::Int64, ::Float64)Se generan constructores internos y externos por defecto para cada T:
struct Punto{T<:Real}
x::T
y::T
Punto{T}(x,y) where {T<:Real} = new(x,y)
end
Punto(x::T, y::T) where {T<:Real} = Punto{T}(x,y);y tanto x como y deben ser del mismo tipo.
Cuando x e y son de tipos diferentes, se puede definir el siguiente constructor externo:
Punto(x::Real, y::Real) = Punto(promote(x,y)...);La función promote se detalla en Sección 19.8.2.
Conversión y Promoción
Julia tiene un sistema para convertir argumentos de diferentes tipos a un tipo común. Esto es llamado promoción, y aunque no es automático, se puede realizar fácilmente.
Conversión
Un valor se puede convertir de un tipo a otro:
julia> x = 12
12
julia> typeof(x)
Int64
julia> convert(UInt8, x)
0x0c
julia> typeof(ans)
UInt8Se pueden agregar nuestros propios métodos convert:
julia> Base.convert(::Type{Punto{T}}, x::Array{T, 1}) where {T<:Real} = Punto(x...)
julia> convert(Punto{Int64}, [1, 2])
Punto{Int64}(1, 2)Promoción
Promoción es la conversión de valores de diferentes tipos a un solo tipo común:
julia> promote(1, 2.5, 3)
(1.0, 2.5, 3.0)Generalmente, los métodos para la función promote no se definen directamente, sino que se usa la función auxiliar promot_rule para especificar las reglas de la promoción:
promote_rule(::Type{Float64}, ::Type{Int32}) = Float64Metaprogramación
Un código de Julia se puede representar como una estructura de datos del mismo lenguaje. Esto permite que un programa escriba y manipule su propio código.
Expresiones
Cada programa de Julia comienza como una cadena:
julia> prog = "1 + 2"
"1 + 2"El siguiente paso es analizar cada cadena en un objeto llamado expresión, representado por el tipo de Julia Expr:
julia> ex = Meta.parse(prog)
:(1 + 2)
julia> typeof(ex)
Expr
julia> dump(ex)
Expr
head: Symbol call
args: Array{Any}((3,))
1: Symbol +
2: Int64 1
3: Int64 2La función dump muestra objetos expr con anotaciones.
Las expresiones se pueden construir directamente con el prefijo : entre paréntesis o usando un bloque quote:
julia> ex = quote
1 + 2
end;eval
Julia puede evaluar un objeto de expresión usando la función eval:
julia> eval(ex)
3Cada módulo tiene su propia función eval que evalúa las expresiones de su ámbito.
|
Aviso
|
Generalmente si un código tiene muchas llamadas a |
Macros
Las macros pueden incluir código generado en un programa. Una macro asocia una tupla de objetos Expr directamente con una expresión compilada:
Aquí hay una macro simple:
macro contenedorvariable(contenedor, elemento)
return esc(:($(Symbol(contenedor,elemento)) = $contenedor[$elemento]))
endLas macros se llaman anteponiendo @ (arroba) a su nombre. La llamada a la macro @contenedorvariable letras 1 se reemplaza por:
:(letras1 = letras[1])@macroexpand @contenedorvariable letras 1 returns this expression which is extremely useful for debugging.
Este ejemplo ilustra cómo una macro puede acceder al nombre de sus argumentos, algo que una función no puede hacer. Se debe "escapar" de la expresión de retorno con esc porque debe resolverse en el entorno de la macro llamada.
|
Nota
|
¿Por qué usar Macros? Las macros generan e incluyen fragmentos de código personalizado durante el tiempo de análisis, es decir, antes de ejecutar el programa completo. |
Funciones Generadas
La macro @generated crea código especializado para métodos dependiendo del tipo de los argumentos:
@generated function cuadrado(x)
println(x)
:(x * x)
endEl cuerpo devuelve una expresión citada como una macro.
Para la sentencia que llama, la función generada se comporta como una función normal:
julia> x = cuadrado(2); # nota: la salida es de la instrucción println () que está en el cuerpo
Int64
julia> x # ahora imprimimos x
4
julia> y = cuadrado("spam");
String
julia> y
"spamspam"Datos Faltantes
Los datos faltantes se pueden representar a través del objeto missing, que es la instancia única del tipo Missing.
Los arreglos pueden contener datos que faltan, missing values en inglés:
julia> a = [1, missing]
2-element Array{Union{Missing, Int64},1}:
1
missingEl tipo de dicho arreglo es Union{Missing, T}, dónde T es el tipo de los valores que realmente tenemos en el arreglo.
Las funciones de reducción devuelven missing cuando se invocan con arreglos que contienen valores que faltan
julia> sum(a)
missingEn este caso, se puede usar la función skipmissing para omitir los valores que faltan:
julia> sum(skipmissing([1, missing]))
1Llamar a Código de C y Fortran
Se escribe mucho código en C o Fortran. Reutilizar un código que ya ha sido probado generalmente es mejor que escribir su propia versión en otro lenguaje. Julia puede llamar directamente a las bibliotecas C o Fortran existentes utilizando la sintaxis ccall.
En Sección 14.6 se presentó una interfaz de Julia de la biblioteca GDBM de funciones de base de datos. La biblioteca está escrita en C. Para cerrar la base de datos, se debe hacer una llamada a la función close(db):
Base.close(dbm::DBM) = gdbm_close(dbm.handle)
function gdbm_close(handle::Ptr{Cvoid})
ccall((:gdbm_close, "libgdbm"), Cvoid, (Ptr{Cvoid},), handle)
endUn objeto dbm tiene un atributo handle de tipo Ptr{Cvoid}. Este atributo contiene un puntero de C que apunta a la base de datos. Para cerrar la base de datos, debe llamarse a la función de C gdbm_close teniendo como único argumento el puntero C apuntando a la base de datos, sin valor de retorno. Julia hace esto directamente con la función ccall que tiene como argumentos:
-
una tupla que consiste en un símbolo que contiene el nombre de la función que queremos llamar:
:gdbm_closey la librería compartida especificada como una cadena:+"libgdm", -
el tipo de retorno:
Cvoid, -
una tupla de tipos de argumentos:
(Ptr{Cvoid},) -
los valores del argumento:
handle.
Una visión completa de la librería GDBM se puede encontrar como ejemplo en las fuentes de ThinkJulia.
Glossary
- clausura
-
Función que captura variables del ámbito en dónde está definida.
- bloque let
-
Bloque de asignación de nuevas ligaduras variables.
- función anónima
-
Función definida sin nombre.
- tupla con nombre
-
Tupla con componentes con nombre.
- argumentos con nombre
-
Argumentos identificados por su nombre en vez de solo por la posición que ocupan.
- bloque do
-
Construcción usada para definir y llamar a una función anónima parecida a un bloque de código normal.
- operador ternario
-
Operador de estructura de control que toma tres operandos: una condición, una expresión que se ejecutará si la condición devuelve
truey una expresión que se ejecutará si la condición devuelvefalse. - evaluación de cortocircuito
-
Evaluación de un operador booleano para el que se ejecuta o evalúa el segundo argumento solo si el primero no es suficiente para determinar el valor de la expresión.
- tareas (corrutina)
-
Característica de las estructuras de control que permite suspender y reanudar cálculos de manera flexible.
- tipo primitivo
-
Tipo concreto cuyos datos están compuestos de bits.
- unión de tipos
-
Tipo que incluye todas las instancias de cualquiera de sus tipos de parámetros como objetos.
- tipo paramétrico
-
Tipo que tiene parámetros.
- funtor
-
Objeto con un método asociado, para que sea invocable.
- conversión
-
Permite convertir un valor de un tipo a otro.
- promoción
-
Conversión de valores de diferentes tipos a un solo tipo común.
- expresión
-
Tipo de Julia que contiene una construcción de lenguaje.
- macro
-
Forma de incluir el código generado en el cuerpo final de un programa.
- funciones generadas
-
Funciones capaces de generar código especializado según el tipo de los argumentos.
- datos faltantes
-
Instancias que representan datos sin valor.
20. Extra: Base y Librería Estándar
Julia tiene todo lo necesario. El módulo Base contiene las funciones, tipos y macros más útiles, los cuales están disponibles directamente en Julia.
Julia también posee una gran cantidad de módulos especializados en su Biblioteca Estándar (módulos para fechas, computación distribuida, álgebra lineal, perfiles, números aleatorios, entre otros). Las funciones, los tipos y las macros definidos en la Biblioteca Estándar deben importarse antes de poder usarse:
-
import Moduleimporta el modulo, yModule.fn(x)llama a la funciónfn -
using Moduleimporta todas las funciones, tipos y macros exportadas deModule.
Además, es posible agregar más funciones a una gran cantidad de paquetes (https://juliaobserver.com).
Este capítulo no es un reemplazo de la documentación oficial de Julia. Sólo se dan algunos ejemplos para ilustrar lo que es posible hacer, sin ser exhaustivo. Las funciones ya vistas no están incluidas. Se puede encontrar una explicación más completa en https://docs.julialang.org.
Midiendo el Rendimiento
Hemos visto que algunos algoritmos funcionan mejor que otros. fibonnaci en Sección 11.6 es mucho más rápido que fib en Sección 6.7. La macro @time permite cuantificar la diferencia:
julia> fib(1)
1
julia> fibonacci(1)
1
julia> @time fib(40)
0.567546 seconds (5 allocations: 176 bytes)
102334155
julia> @time fibonacci(40)
0.000012 seconds (8 allocations: 1.547 KiB)
102334155@time imprime el tiempo que tardó en ejecutarse la función, el número de asignaciones (allocations) y la memoria asignada antes de devolver el resultado. La función fibonacci, que guarda resultados previos, es mucho más rápida pero necesita más memoria.
El teorema "No free lunch" dice que no existe un único modelo que funcione mejor en todos los casos.
|
Observación
|
Para comparar dos algoritmos, estos deben implementarse como funciones. Una función en Julia se compila la primera vez que se ejecuta, por lo tanto, se debe excluir la primera vez que se llama a estas funciones al medir el rendimiento. De lo contrario, también se mediría el tiempo de compilación. El paquete |
Colecciones y Estructuras de Datos
En Sección 13.6 se usan diccionarios para encontrar las palabras que aparecían en un documento y que no aparecían en un arreglo de palabras. La función que se escribió tomaba d1, que contenía las palabras del documento como claves, y d2, que contenía el arreglo de palabras. Y devolvía un diccionario que contenía las claves de d1 que no estaban en d2.
function resta(d1, d2)
res = Dict()
for clave in keys(d1)
if clave ∉ keys(d2)
res[clave] = nothing
end
end
res
endEn todos estos diccionarios, los valores son nothing porque nunca son usados. Con esto se está desperdiciando espacio de almacenamiento.
Julia ofrece otro tipo integrado llamado conjunto, que se comporta como una colección de claves de diccionario sin valores. Agregar elementos a un conjunto es rápido y también lo es verificar si un elemento forma parte de él. Además, los conjuntos proporcionan funciones y operadores para calcular operaciones de conjuntos.
Por ejemplo, la resta de conjuntos está disponible como una función llamada setdiff. Entonces reescribiendo resta:
function resta(d1, d2)
setdiff(d1, d2)
endEl resultado es un conjunto en vez de un diccionario.
Algunos de los ejercicios en este libro se pueden hacer de manera eficiente y concisa con conjuntos. Por ejemplo, a continuación se muestra una solución para repetido, de Sección 10.15.7, que usa un diccionario:
function repetido(t)
d = Dict()
for x in t
if x ∈ d
return true
end
d[x] = nothing
end
false
endCuando un elemento aparece por primera vez, se agrega al diccionario. Si el mismo elemento aparece nuevamente, la función devuelve true.
Usando conjuntos, podemos escribir la misma función:
function repetido(t)
length(Set(t)) < length(t)
endUn elemento solo puede aparecer en un conjunto una vez, por lo que si un elemento en t aparece más de una vez, el conjunto será más pequeño que t. Si no hay elementos repetidos, el conjunto tendrá el mismo tamaño que t.
También podemos usar conjuntos para hacer algunos de los ejercicios de Capítulo 9. Por ejemplo, aquí hay una versión de usasolo con un bucle:
function usasolo(palabra, disponibles)
for letra in palabra
if letra ∉ disponibles
return false
end
end
true
endusasolo comprueba si todas las letras en palabra están en disponibles. Podemos reescribir esta función:
function usasolo(palabra, disponibles)
Set(palabra) ⊆ Set(disponibles)
endEl operador ⊆ (\subseteq TAB) verifica si un conjunto es un subconjunto de otro, incluida la posibilidad de que sean iguales, lo cual es cierto si todas las letras en palabra aparecen en disponibles.
Exercise 20-1
Reescriba la función evita de Capítulo 9 usando conjuntos.
Matemáticas
También se pueden usar números complejos en Julia. La constante global im está asociada al número complejo \(\mathrm{i}\), que representa la raíz cuadrada principal de \(-1\).
Ahora se puede verificar la identidad de Euler,
julia> ℯ^(im*π)+1
0.0 + 1.2246467991473532e-16imEl símbolo ℯ (\euler TAB) es la base de los logaritmos naturales.
Se puede analizar la naturaleza compleja de las funciones trigonométricas:
Se puede probar esta fórmula para diferentes valores de \(x\).
julia> x = 0:0.1:2π
0.0:0.1:6.2
julia> cos.(x) == 0.5*(ℯ.^(im*x)+ℯ.^(-im*x))
trueAquí se muestra otro ejemplo del operador punto. Julia también permite usar valores numéricos con identificadores (símbolos léxicos que nombran entidades, como π) como en 2π.
Cadenas
En Capítulo 8 y Capítulo 9, se realizan algunas búsquedas en cadenas. Además, Julia puede usar expresiones regulares (o regexes) compatibles con Perl, lo que facilita la tarea de encontrar patrones complejos en cadenas.
La función usasolo se puede implementar como una expresión regular:
function usasolo(palabra, disponibles)
r = Regex("[^$(disponibles)]")
!occursin(r, palabra)
endLa expresión regular busca un carácter que no está en la cadena disponible y occursin devuelve true si el patrón se encuentra en palabra.
julia> usasolo("banana", "abn")
true
julia> usasolo("bananas", "abn")
falseLas expresiones regulares también se pueden construir como literales de cadena no estándar con el prefijo r:
julia> match(r"[^abn]", "banana")
julia> m = match(r"[^abn]", "bananas")
RegexMatch("s")En este caso, la interpolación de cadenas no está permitida. La función match devuelve nothing si no se encuentra el patrón, de lo contrario, devuelve un objeto regexmatch.
Podemos extraer la siguiente información de un objeto regexmatch:
-
La subcadena que coincide:
m.match -
Las subcadenas que coinciden en forma de arreglo de cadenas:
m.captures -
La primera posición en la que se encuentra el patrón:
m.offset -
Las posiciones de las subcadenas que coinciden en forma de arreglo:
m.offsets
julia> m.match
"s"
julia> m.offset
7Las expresiones regulares son extremadamente poderosas y el manual de PERL http://perldoc.perl.org/perlre.html explica cómo realizar hasta las búsquedas más extrañas.
Arreglos
En el Capítulo 10 se usa un objeto de arreglo unidimensional, con un índice para acceder a sus elementos. Sin embargo, en Julia las matrices son multidimensionales.
Se puede crear una matriz de ceros de 2 por 3:
julia> z = zeros(Float64, 2, 3)
2×3 Array{Float64,2}:
0.0 0.0 0.0
0.0 0.0 0.0
julia> typeof(z)
Array{Float64,2}El tipo de esta matriz es un arreglo que contiene números de punto flotante. Esta matriz es de 2 dimensiones.
La función size devuelve una tupla con el número de elementos en cada dimensión:
julia> size(z)
(2, 3)La función ones construye una matriz con elementos de valor unitario:
julia> s = ones(String, 1, 3)
1×3 Array{String,2}:
"" "" ""El elemento de valor unitario de una cadena es una cadena vacía.
|
Aviso
|
|
Se puede crear una matriz usando espacios para separar elementos en una fila, y punto y coma ; para separar filas:
julia> a = [1 2 3; 4 5 6]
2×3 Array{Int64,2}:
1 2 3
4 5 6Se pueden usar corchetes para modificar elementos de una matriz:
julia> z[1,2] = 1
1
julia> z[2,3] = 1
1
julia> z
2×3 Array{Float64,2}:
0.0 1.0 0.0
0.0 0.0 1.0Se pueden usar porciones en cada dimensión para seleccionar un subgrupo de elementos:
julia> u = z[:,2:end]
2×2 Array{Float64,2}:
1.0 0.0
0.0 1.0El operador . aplica una operación en todas las dimensiones:
julia> ℯ.^(im*u)
2×2 Array{Complex{Float64},2}:
0.540302+0.841471im 1.0+0.0im
1.0+0.0im 0.540302+0.841471imInterfaces
Julia especifica algunas interfaces informales para definir comportamientos, es decir, métodos con un objetivo específico. Cuando se extienden estos métodos para un tipo, los objetos de ese tipo se pueden usar para construir estos comportamientos.
Si parece un pato, nada como un pato y grazna como un pato, entonces probablemente sea un pato.
En Sección 6.7 implementamos la función fib que devuelve el elemento \(n\)-ésimo de la secuencia de Fibonnaci.
Recorrer los valores de una colección, lo cual recibe el nombre de iteración, es una interfaz de este tipo. Se puede crear un iterador que devuelva la secuencia de Fibonacci:
struct Fibonacci{T<:Real} end
Fibonacci(d::DataType) = d<:Real ? Fibonacci{d}() : error("No Real type!")
Base.iterate(::Fibonacci{T}) where {T<:Real} = (zero(T), (one(T), one(T)))
Base.iterate(::Fibonacci{T}, state::Tuple{T, T}) where {T<:Real} = (state[1], (state[2], state[1] + state[2]))Se implementa un tipo paramétrico Fibonacci sin atributos, un constructor externo y dos métodos iterate. Se llama al primer método iterate para inicializar el iterador, y este devuelve una tupla que consta de un primer valor: 0, y un estado. El estado en este caso es una tupla que contiene el segundo y el tercer valor: 1 y 1.
Se llama al segundo método iterate para obtener el siguiente valor de la secuencia de Fibonacci, y devuelve una tupla que tiene como primer elemento el siguiente valor y como segundo elemento el estado que es una tupla con los dos valores siguientes.
Ahora se puede usar Fibonacci en un bucle for:
julia> for e in Fibonacci(Int64)
e > 100 && break
print(e, " ")
end
0 1 1 2 3 5 8 13 21 34 55 89Parece sacado debajo de la manga, pero la explicación es simple. Un bucle for en Julia
for i in iter
# body
endse traduce en:
next = iterate(iter)
while next !== nothing
(i, state) = next
# body
next = iterate(iter, state)
endEste es un ejemplo de cómo una interfaz bien definida permite que una implementación use todas las funciones disponibles en esta interfaz.
Módulo Interactive Utilities
Ya se ha visto el módulo InteractiveUtils en Sección 18.10. La macro @which es solo una de las tantas opciones.
La biblioteca LLVM transforma el código de Julia en código de máquina, en varios pasos. Podemos visualizar la salida de cada etapa.
Aquí se muestra un ejemplo simple:
function sumacuadrada(a::Float64, b::Float64)
a^2 + b^2
endEl primer paso es mirar el código de bajo nivel (lowered code):
julia> using InteractiveUtils
julia> @code_lowered sumacuadrada(3.0, 4.0)
CodeInfo(
1 ─ %1 = Core.apply_type(Base.Val, 2)
│ %2 = (%1)()
│ %3 = Base.literal_pow(:^, a, %2)
│ %4 = Core.apply_type(Base.Val, 2)
│ %5 = (%4)()
│ %6 = Base.literal_pow(:^, b, %5)
│ %7 = %3 + %6
└── return %7
)La macro @code_lowered devuelve un arreglo de una representación intermedia del código que utiliza el compilador para generar código optimizado.
El siguiente paso añade información del tipo:
julia> @code_typed sumacuadrada(3.0, 4.0)
CodeInfo(
1 ─ %1 = Base.mul_float(a, a)::Float64
│ %2 = Base.mul_float(b, b)::Float64
│ %3 = Base.add_float(%1, %2)::Float64
└── return %3
) => Float64El tipo de resultados intermedios y el valor de retorno se infiere correctamente.
Esta representación del código se transforma en código LLVM:
julia> @code_llvm sumacuadrada(3.0, 4.0)
; @ none:1 within `sumacuadrada'
define double @julia_sumacuadrada_6080(double, double) {
top:
; @ none:2 within `sumacuadrada'
; ┌ @ intfuncs.jl:296 within `literal_pow'
; │┌ @ float.jl:405 within `*'
%2 = fmul double %0, %0
%3 = fmul double %1, %1
; └└
; ┌ @ float.jl:401 within `+'
%4 = fadd double %2, %3
; └
ret double %4
}Y finalmente se genera el código de máquina:
julia> @code_native sumacuadrada(3.0, 4.0)
.text
; ┌ @ none:2 within `sumacuadrada'
; │┌ @ intfuncs.jl:296 within `literal_pow'
; ││┌ @ float.jl:405 within `*'
vmulsd %xmm0, %xmm0, %xmm0
vmulsd %xmm1, %xmm1, %xmm1
; │└└
; │┌ @ float.jl:401 within `+'
vaddsd %xmm1, %xmm0, %xmm0
; │└
retq
nopl (%rax)
; └Depuración
Las macros Logging son una alternativa al andamiaje con sentencias de impresión:
julia> @warn "¡Oh vosotros los que entráis, abandonad la depuración con printf!"
┌ Warning: ¡Oh vosotros los que entráis, abandonad la depuración con printf!
└ @ Main REPL[1]:1Las sentencias de depuración (debug) no tienen que eliminarse del código. Por ejemplo, en contraste con el @warn anterior,
julia> @debug "La suma de algunos valores $(sum(rand(100)))"debug por defecto no produce salida. En este caso, sum(rand(100)) nunca se evaluará a menos que debug logging esté habilitado.
El nivel de logging puede seleccionarse mediante la variable de entorno JULIA_DEBUG:
$ JULIA_DEBUG=all julia -e '@debug "La suma de algunos valores $(sum(rand(100)))"'
┌ Debug: La suma de algunos valores 47.116520814555024
└ @ Main none:1Aquí, hemos utilizado all para obtener toda la información de depuración, pero también se puede optar por generar salida solo para un archivo o módulo específico.
Glosario
- regex
-
Expresión regular, una secuencia de caracteres que definen un patrón de búsqueda.
- matriz
-
Arreglo bidimensional.
- representación intermedia
-
Estructura de datos utilizada internamente por un compilador para representar el código fuente.
- código de máquina
-
Instrucciones que pueden ser ejecutadas directamente por la unidad central de procesamiento de una computadora.
- debug logging
-
Almacenar mensajes de depuración en un registro (log).
21. Depuración
Al depurar, es necesario distinguir entre los diferentes tipos de errores para rastrearlos más rápidamente:
-
Los errores de sintaxis se descubren cuando el intérprete traduce el código fuente a código de bytes. Estos errores indican que hay una falla en la estructura del programa. Por ejemplo, omitir la palabra reservada
endal final de un bloque de funciones genera el mensajeERROR: LoadError: syntax: incomplete: function requires end. -
Los errores en tiempo de ejecución se presentan si algo falla mientras se ejecuta el programa. La mayoría de los mensajes de error en tiempo de ejecución indican dónde ocurrió el error y qué funciones se estaban ejecutando. Ejemplo: Una recursión infinita eventualmente causa el error en tiempo de ejecución
ERROR: StackOverflowError. -
Los errores semánticos ocurren cuando un programa se ejecuta sin generar mensajes de error pero no hace lo que debería. Por ejemplo: una expresión puede no evaluarse en el orden esperado, generando un resultado incorrecto.
El primer paso en la depuración es averiguar el tipo de error al que se enfrenta. Aunque las siguientes secciones están organizadas por tipo de error, algunas técnicas son aplicables en más de una situación.
Errores de Sintaxis
Los errores de sintaxis suelen ser fáciles de corregir una vez se descubre cuáles son. Desafortunadamente, muchas veces los mensajes de error no son útiles. Los mensajes más comunes son
ERROR: LoadError: syntax: incomplete: premature end of input
y
ERROR: LoadError: syntax: unexpected "=",
los cuales no son muy informativos.
Por otro lado, el mensaje indica en qué parte del programa se produjo el problema. En realidad, indica dónde Julia notó que había un problema, que no es necesariamente dónde está el error. A veces, el error es anterior a la ubicación del mensaje de error, generalmente en la línea anterior.
Si está programando incrementalmente, el usuario debería tener casi localizado el error ya que estará en la última línea que agregó.
Si está copiando código de un libro, comience comparando su código con el código del libro y verifique cada letra. Al mismo tiempo, recuerde que el libro puede contener errores, por lo que si ve algo que parece un error de sintaxis, es posible que lo sea.
Aquí hay algunas formas de evitar los errores de sintaxis más comunes:
-
Asegúrese de no estar usando una palabra reservada de Julia en un nombre de variable.
-
Compruebe que tiene la palabra reservada
endal final de cada sentencia compuesta, incluyendo los bloquesfor,while,ifyfunction. -
Asegúrese de que las cadenas tengan su par de comillas de apertura y cierre. Asegúrese de que todas las comillas sean "comillas rectas", y no otro tipo de "comillas".
-
Si tiene cadenas que ocupan varias líneas con triples comillas, asegúrese de que ha terminado la cadena correctamente. Una cadena sin terminar puede provocar un error invalid token al final de su programa, o puede hacer que la siguiente parte del programa sea tratada como una cadena hasta llegar a la siguiente cadena. ¡El segundo caso podría no presentar mensaje de error!
-
Un paréntesis sin cerrar —
(,{, or[— hace que Julia continúe con la línea siguiente como parte de la sentencia actual. Generalmente, se produce un error casi inmediatamente en la siguiente línea. -
Verifique el clásico error que se produce al ocupar
=en lugar de==dentro de un condicional. -
Si tiene caracteres que no son ASCII en el código (incluidas cadenas y comentarios), esto podría causar un problema, aunque Julia generalmente maneja caracteres no ASCII. Tenga cuidado si pega texto de una página web u otra fuente.
Si nada funciona, pase a la siguiente sección …
Sigo haciendo cambios y no hay diferencia
Si el REPL dice que hay un error y usted no lo ve, podría deberse a que usted y el REPL no están viendo el mismo código. Verifique su entorno de programación para asegurarse de que el programa que está editando es el que Julia está tratando de ejecutar.
Si no está seguro, intente poner un error de sintaxis obvio y deliberado al comienzo del programa. Ahora ejecútelo de nuevo. Si REPL no encuentra el nuevo error, no está ejecutando el nuevo código.
Estas son algunas de las posibles razones:
-
Editó el archivo y olvidó guardar los cambios antes de ejecutarlo nuevamente. Algunos entornos de programación hacen esto por usted, pero otros no.
-
Cambió el nombre del archivo, pero aún está ejecutando el archivo con el nombre anterior.
-
Algo en su entorno de desarrollo está configurado incorrectamente.
-
Si está escribiendo un módulo y está usando
using, asegúrese de no darle a su módulo el mismo nombre que uno de los módulos estándar de Julia. -
Si está usando
usingpara importar un módulo, recuerde que debe reiniciar REPL cuando modifique el código en el módulo. Si vuelve a importar el módulo, no ocurre nada.
Si se queda atascado y no puede darse cuenta de lo que está sucediendo, un enfoque es comenzar de nuevo con un nuevo programa como "¡Hola, Mundo!" y asegurarse de que puede ejecutar este programa ya conocido. Luego, puede agregar gradualmente las piezas del programa original al nuevo.
Errores en Tiempo de Ejecución
Una vez que su programa es sintácticamente correcto, Julia puede leerlo y al menos comenzar a ejecutarlo. ¿Qué podría salir mal?
Mi programa no hace absolutamente nada
Este problema es común cuando su archivo consta de funciones y clases, pero en realidad no llama a ninguna función para iniciar la ejecución. Esto puede ser intencional si sólo se busca importar este módulo para suministrar clases y funciones.
Si no es intencional, asegúrese de que haya una llamada a la función en el programa, y asegúrese de que el flujo de ejecución pase por esta llamada (vea Sección 21.2.2.3).
Mi programa se congela
Si un programa se detiene y parece no estar haciendo nada, está "congelado". Generalmente eso significa que está atrapado en un bucle infinito o en una recursión infinita.
-
Si hay un bucle en particular que le resulta sospechoso de poder provocar el problema, agregue una sentencia de impresión justo antes del bucle que diga "entrando al bucle" y otra inmediatamente posterior que diga "saliendo del bucle".
Ejecute el programa. Si recibe el primer mensaje y no el segundo, tiene un bucle infinito. Vea Sección 21.2.2.1.
-
La mayoría de las veces, una recursión infinita hará que el programa se ejecute por un rato y luego produzca un error
ERROR: LoadError: StackOverflowError. Si eso sucede, vea Sección 21.2.2.2.Si no obtiene este error pero sospecha que hay un problema con un método o función recursiva, igual puede utilizar las técnicas de Sección 21.2.2.2.
-
Si ninguno de esos pasos funciona, comience a probar otros bucles, y otras funciones y métodos recursivos.
-
Si esto no funciona, quizás es porque usted no entiende el flujo de ejecución de su programa. Vea Sección 21.2.2.3.
Bucle Infinito
Si cree tener un bucle infinito y cree saber cuál es, añada una sentencia de impresión que imprima los valores de las variables de la condición al final del bucle junto con el valor de la condición.
Por ejemplo:
while x > 0 && y < 0
# hacer algo con x
# hacer algo con y
@debug "variables" x y
@debug "condicion" x > 0 && y < 0
endAhora, cuando ejecute el programa en modo de depuración, verá el valor de las variables y la condición en cada iteración. En la última iteración, la condición debe ser false. Si el ciclo continúa, podrá ver los valores de x e y, y podrá averiguar por qué no se actualizan correctamente.
Recursión Infinita
La mayoría de las veces, una recursión infinita hace que el programa se ejecute durante un tiempo y luego produzca un error
ERROR: LoadError: StackOverflowError.
Si sospecha que una función o un método está causando una recursión infinita, comience por asegurarse de que hay un caso base. En otras palabras, debería haber una condición que haga que la función devuelva un valor sin hacer otra llamada recursiva. Si no, necesita revisar el algoritmo y encontrar ese caso base.
Si hay un caso base pero el programa no parece llegar hasta él, añada una sentencia de impresión al inicio de la función que imprima los parámetros. Ahora, cuando ejecute el programa, verá el valor de los parámetros cada vez que se llame la función. Si los parámetros no se acercan al caso base, eso le dará alguna idea de por qué no lo hace.
Flujo de Ejecución
Si no está seguro del flujo de ejecución en su programa, añada sentencias de impresión al principio de cada función con mensajes como “entrando a la función fun”, donde fun sea el nombre de la función.
Ahora, cuando ejecute el programa, se imprimirá una mensaje en cada función a medida que estas sean llamadas.
Cuando ejecuto el programa recibo una excepción.
Si algo sale mal durante la ejecución, Julia imprime un mensaje que incluye el nombre de la excepción, la línea del programa donde sucedió el problema y un trazado inverso.
El trazado inverso identifica la función que se está ejecutando y la función que la llamó, y luego la función que llamó a esa, y así sucesivamente. En otras palabras, traza la ruta de las llamadas a las funciones que le llevaron a donde se encuentra. También incluye los números de las líneas de su archivo dónde suceden todas esas llamadas.
El primer paso es examinar el lugar del programa donde ocurrió el error y ver si puede adivinar lo que sucedió. Estos son algunos de los errores en tiempo de ejecución más comunes:
- ArgumentError
-
Uno de los argumentos para llamar a una función no tiene la forma esperada.
- BoundsError
-
Se está tratando de acceder a un elemento de un arreglo fuera de los límites de indexación.
- DomainError
-
El argumento de una función o constructor no pertenece al dominio válido.
- DivideError
-
Se intentó dividir un entero por 0.
- EOFError
-
No había más datos disponibles para leer desde un archivo o stream.
- InexactError
-
No se puede convertir a un tipo.
- KeyError
-
Se está tratando de acceder o eliminar un elemento inexistente de un objeto
AbstractDict(Dict) oSet. - MethodError
-
No existe un método con la especificación de tipo requerida en la función genérica dada. Alternativamente, no existe un método único más específico.
- OutOfMemoryError
-
Una operación asignó demasiada memoria para que el sistema o el recolector de basura opere correctamente.
- OverflowError
-
El resultado de una expresión es demasiado grande para el tipo especificado y se produce un desbordamiento.
- StackOverflowError
-
Una llamada a función trata de usar más espacio que el que está disponible en la pila de llamadas. Esto generalmente ocurre cuando una llamada se repite infinitamente.
- StringIndexError
-
Se produjo un error al intentar acceder a un índice inválido de una cadena.
- SystemError
-
Falló una llamada al sistema, y se muestra un mensaje de error.
- TypeError
-
Error de aserción de tipo, o error producido al llamar a una función integrada con un tipo de argumento incorrecto.
- UndefVarError
-
Un símbolo en el entorno (o ámbito) actual no está definido.
Puse tantas sentencias de impresión que me ahogo en información
Uno de los problemas de usar sentencias print en la depuración es que puede terminar ahogado por tanta información. Hay dos formas de resolver esto: simplificar la salida o simplificar el programa.
Para simplificar la salida, puede eliminar o comentar (convertir en comentarios no evaluados cómo órdenes del programa) las sentencias print que no sean útiles o combinarlas. También puede dar a la salida un formato que la haga más comprensible.
Para simplificar el programa puede hacer varias cosas. Primero, puede reducir la escala del problema en el que está trabajando el programa. Por ejemplo, si está buscando algo en una lista, búsquelo en una lista pequeña. Si el programa acepta entradas del usuario, ingrese la entrada más simple que provoque el problema.
Segundo, puede "limpiar" el programa. Elimine el código muerto y reorganice el programa para hacerlo tan legible como sea posible. Por ejemplo, si sospecha que el problema está en una parte del programa con un anidamiento (nesting) muy profundo, pruebe a reescribir esa parte con una estructura más simple. Si sospecha de una función muy larga, trate de dividirla en funciones más pequeñas y pruébelas separadamente.
Generalmente, el proceso de encontrar el caso de prueba mínimo lleva el usuario a encontrar el error. Si encuentra que un programa funciona en una situación pero no en otra, eso le dará una pista sobre lo que está sucediendo.
De forma parecida, reescribir una porción de código puede ayudarle a encontrar errores sutiles. Si realiza un cambio que cree que no debería afectar el programa, pero lo hace, entonces eso puede darle una pista.
Errores Semánticos
En cierto modo, los errores semánticos son los más difíciles de corregir, ya que el intérprete no entrega información sobre lo que está mal. Sólo usted sabe lo que se supone que debe hacer el programa.
El primer paso es hacer una conexión entre el código y el comportamiento que está viendo. Necesita una hipótesis sobre lo que realmente está haciendo el programa. Una de las dificultades que nos encontramos es la alta velocidad de los computadores.
A menudo sería deseable ralentizar el programa a una velocidad humana. El tiempo que lleva colocar unas sentencias print en los lugares adecuados suele ser menor que el que lleva configurar un depurador, poner y quitar puntos de interrupción y “hacer avanzar” al programa hasta donde se produce el error.
Mi programa no funciona
Debería hacerse estas preguntas:
-
¿Hay algo que se supone que debería hacer el programa pero que no sucede? Busque la sección del código que realiza esa función y asegúrese de que se ejecuta cuando debería.
-
¿Ocurre algo que no debería? Busque el código en su programa que realiza esa función y vea si se ejecuta cuando no debe.
-
¿Hay alguna sección del código que cause un efecto que no esperaba? Asegúrese de que entiende el código en cuestión, especialmente si incluye funciones o métodos de otros módulos de Julia. Lea la documentación de las funciones a las que llama. Pruébelas escribiendo casos de prueba simples y comprobando sus resultados.
Para programar necesitará tener un modelo mental de cómo funcionan los programas. Si escribe un programa que no hace lo que esperaba de él, muchas veces el problema no estará en el programa, sino en su modelo mental.
La mejor manera de corregir su modelo mental es dividiendo el programa en sus componentes (normalmente en funciones y métodos) y probando cada componente de forma independiente. Una vez que encuentre la discrepancia entre su modelo y la realidad, podrá solucionar el problema.
Por supuesto, debería ir haciendo y probando componentes a medida que desarrolla el programa. Si encuentra un problema, sólo habría que revisar una pequeña cantidad de código nuevo.
Tengo una expresión grande y peliaguda y no hace lo que espero.
Está bien escribir expresiones complejas mientras sean legibles, pero pueden ser difíciles de depurar. Suele ser una buena idea dividir una expresión compleja en una serie de asignaciones de variables temporales.
Por ejamplo:
agregarcarta(juego.manos[i], sacarcarta(juego.manos[encontrarvecino(juego, i)]))Puede reescribirse como:
vecino = encontrarvecino(juego, i)
cartaseleccionada = sacarcarta(juego.manos[vecino])
agregarcarta(juego.manos[i], cartaseleccionada)La versión explícita es más fácil de leer porque los nombres de variables nos entregan documentación adicional y es más fácil de depurar porque se pueden comprobar los tipos de las variables intermedias y mostrar sus valores.
Otro problema que puede suceder con las expresiones grandes es que el orden de evaluación puede no ser el que usted esperaba. Por ejemplo, si está traduciendo la expresión \(\frac{x}{2\pi}\) a Julia, podría escribir:
y = x / 2 * πEsto no es correcto, ya que la multiplicación y la división tienen la misma precedencia, y se evalúan de izquierda a derecha. De este modo, la anterior expresión calcula \(\frac{x\pi}{2}\).
Una buena forma de depurar expresiones es añadir paréntesis para que sea explícito el orden de evaluación:
y = x / (2 * π)Siempre que no esté seguro del orden de evaluación, utilice paréntesis. El programa no sólo será correcto (en el sentido de que hace lo que usted quiere), sino que además será más legible para otras personas que no hayan memorizado las reglas de precedencia y que lean el código.
Tengo una función que no devuelve lo que esperaba.
Si tiene una sentencia return con una expresión compleja, no tendrá la oportunidad de imprimir el valor de retorno antes de retornar. De nuevo, puede usar una variable temporal. Por ejemplo, en lugar de:
return sacarpares(juego.manos[i])podría escribir:
contar = sacarpares(juego.manos[i])
return contarAhora ya tiene la oportunidad de mostrar el valor de count antes de retornar.
Estoy atascado de verdad y necesito ayuda.
Primero, intente alejarse del computador durante unos minutos. Trabajar con un computador puede provocar estos efectos:
-
Frustración y/o furia.
-
Creencias supersticiosas (“el computador me odia”) y pensamiento mágico (“el programa sólo funciona cuando me pongo la gorra hacia atrás”).
-
Programar dando palos de ciego (el empeño de programar escribiendo todos los programas posibles y eligiendo el que hace lo correcto).
Si se encuentra afectado por alguno de estos síntomas, levántese y dé un paseo. Cuando esté calmado, piense en el programa. ¿Qué es lo que hace? ¿Cuáles pueden ser las causas de tal comportamiento? ¿Cuándo fue la última vez que su programa funcionaba y qué fue lo siguiente que hizo?
A veces lleva tiempo encontrar un error. Muchas veces encontramos errores cuando estamos lejos del computador y divagamos. Algunos de los mejores lugares para encontrar errores son los trenes, las duchas y la cama, justo antes de quedarse dormido.
No, de verdad necesito ayuda
Sucede. Incluso los mejores programadores se atascan de vez en cuando. A veces trabaja durante tanto tiempo en un programa que no puede ver el error. Lo que necesita es un par de ojos nuevos.
Antes de llamar a alguien, asegúrese de estar preparado. Su programa debería ser tan simple como sea posible, y usted debería estar trabajando con la entrada mínima que provoca el error. Debería tener sentencias print en los lugares adecuados (y lo que dicen debería ser comprensible) y debería también entender el problema lo bastante bien como para describirlo de manera concisa.
Cuando llame a alguien para que le ayude, asegúrese de darle la información que necesitan:
-
Si hay un mensaje de error, ¿cuál es y qué parte del programa señala?
-
¿Qué fue lo último que hizo antes de que apareciera el error? ¿Cuáles son las últimas líneas de código que escribió o cuál es el nuevo caso de prueba que falla?
-
¿Qué ha intentado hasta ahora y qué ha averiguado?
Cuando encuentre el error, tómese un momento para pensar acerca de lo que podría haber hecho para encontrarlo más rápido. La siguiente vez que vea algo parecido, será capaz de encontrar el error antes.
Recuerde, el objetivo no es solo hacer que el programa funcione. El objetivo es aprender cómo hacer funcionar el programa.
Apéndice A: Entrada de Unicode
La siguiente tabla muestra algunos de los muchos carácteres Unicode que pueden ingresarse mediante abreviaciones similares a aquellas utilizadas en Latex, en el REPL de Julia (y en muchos otros entornos de edición).
| Carácter | Tab completion sequence | representación ASCII |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Apéndice B: JuliaBox
JuliaBox permite ejecutar Julia en su navegador. Ingrese a la página https://www.juliabox.com, inicie sesión y comience a usar el entorno Jupyter.
La pantalla inicial se muestra en Figura 25. El botón "new" (nuevo) permite la creación de un notebook de Julia, un archivo de texto (text file), una carpeta (folder) o una sesión de terminal (terminal session).
En una sesión de terminal, el comando julia inicia REPL como se muestra en Figura 26.
La interfaz del notebook permite mezclar texto (en modo Markdown) y código con su respectiva salida. Figura 27 muestra un ejemplo.
Puedes encontrar más documentación en el sitio web de Jupyter: http://jupyter.org/documentation.
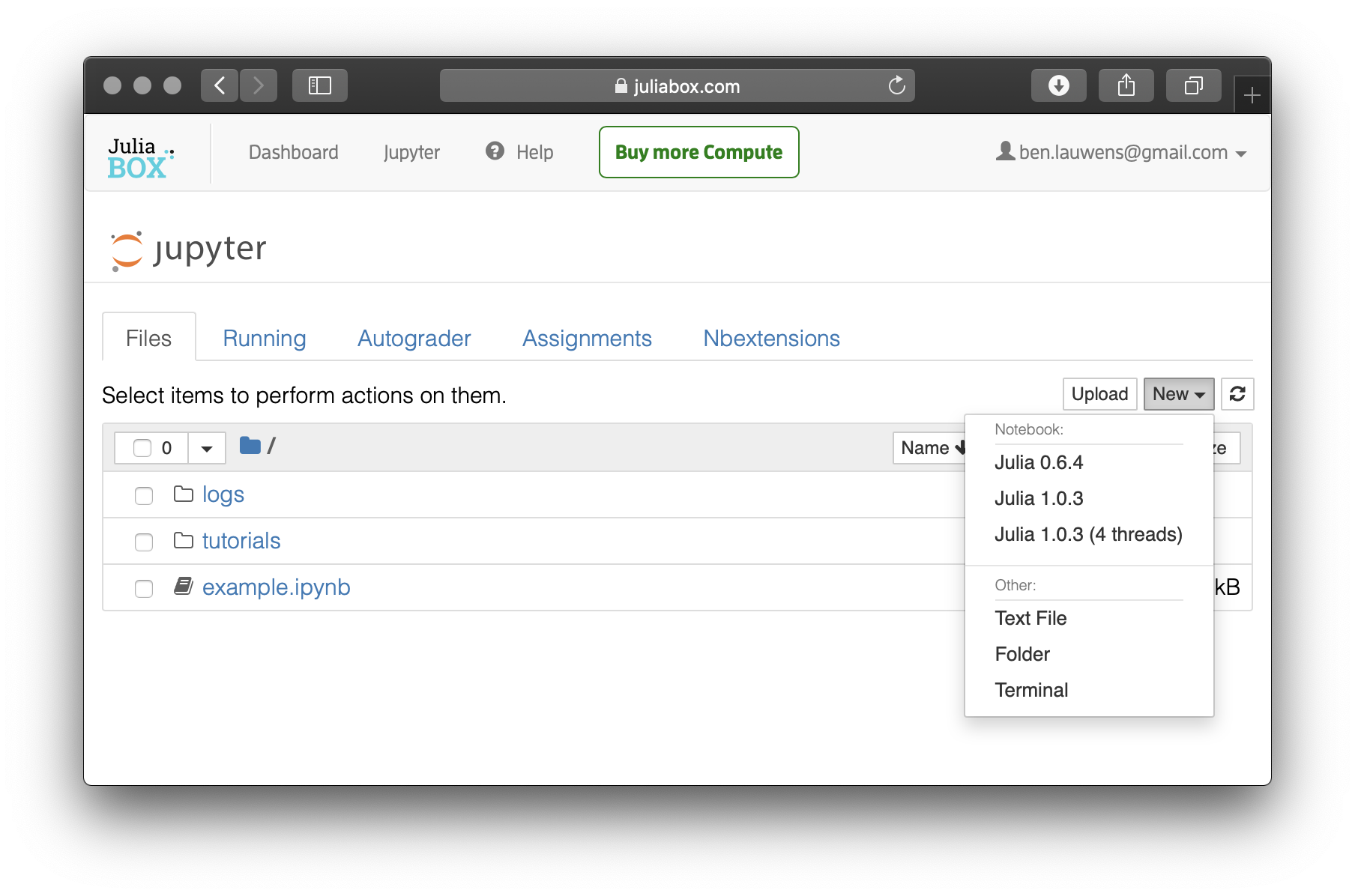
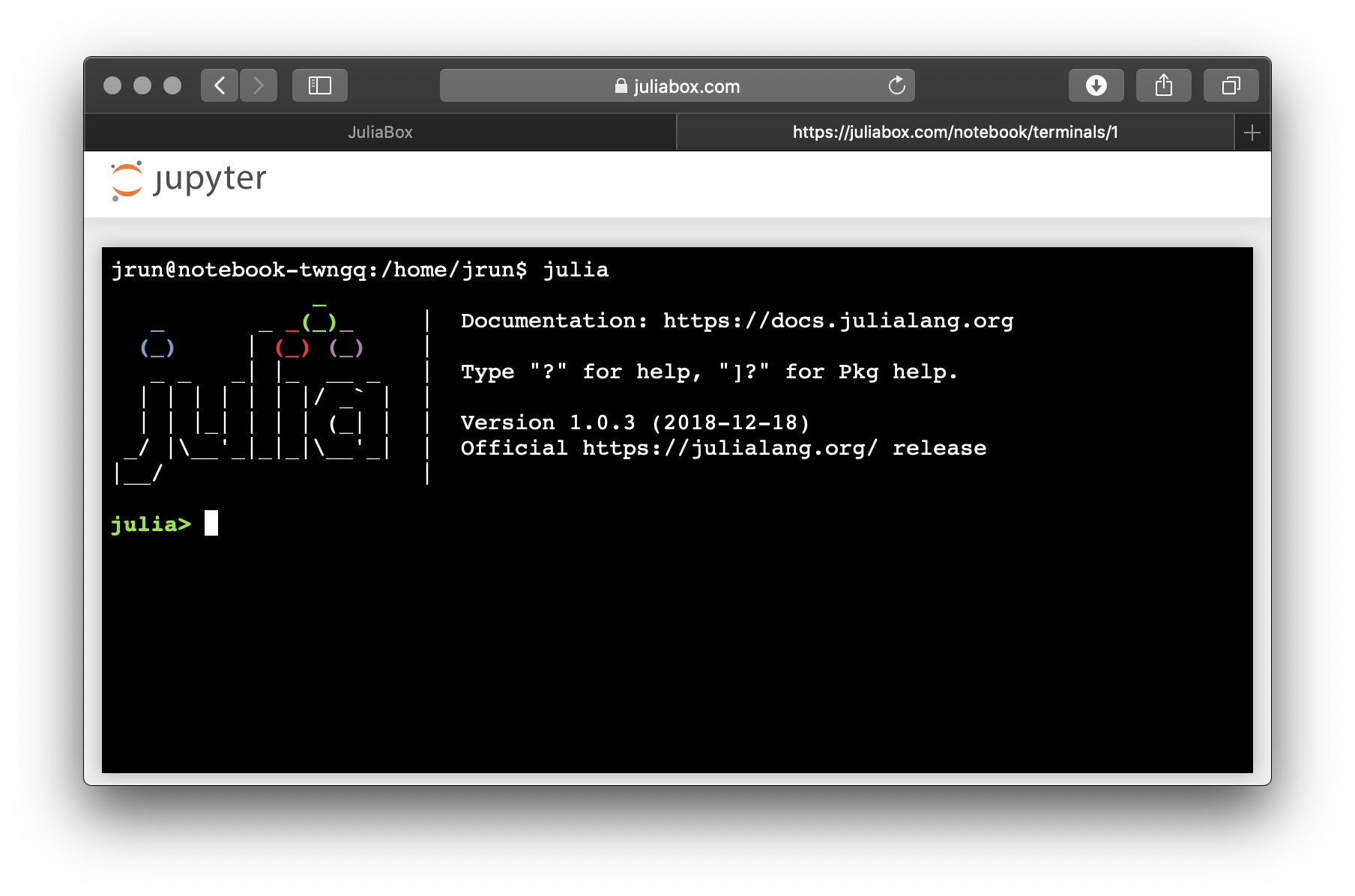
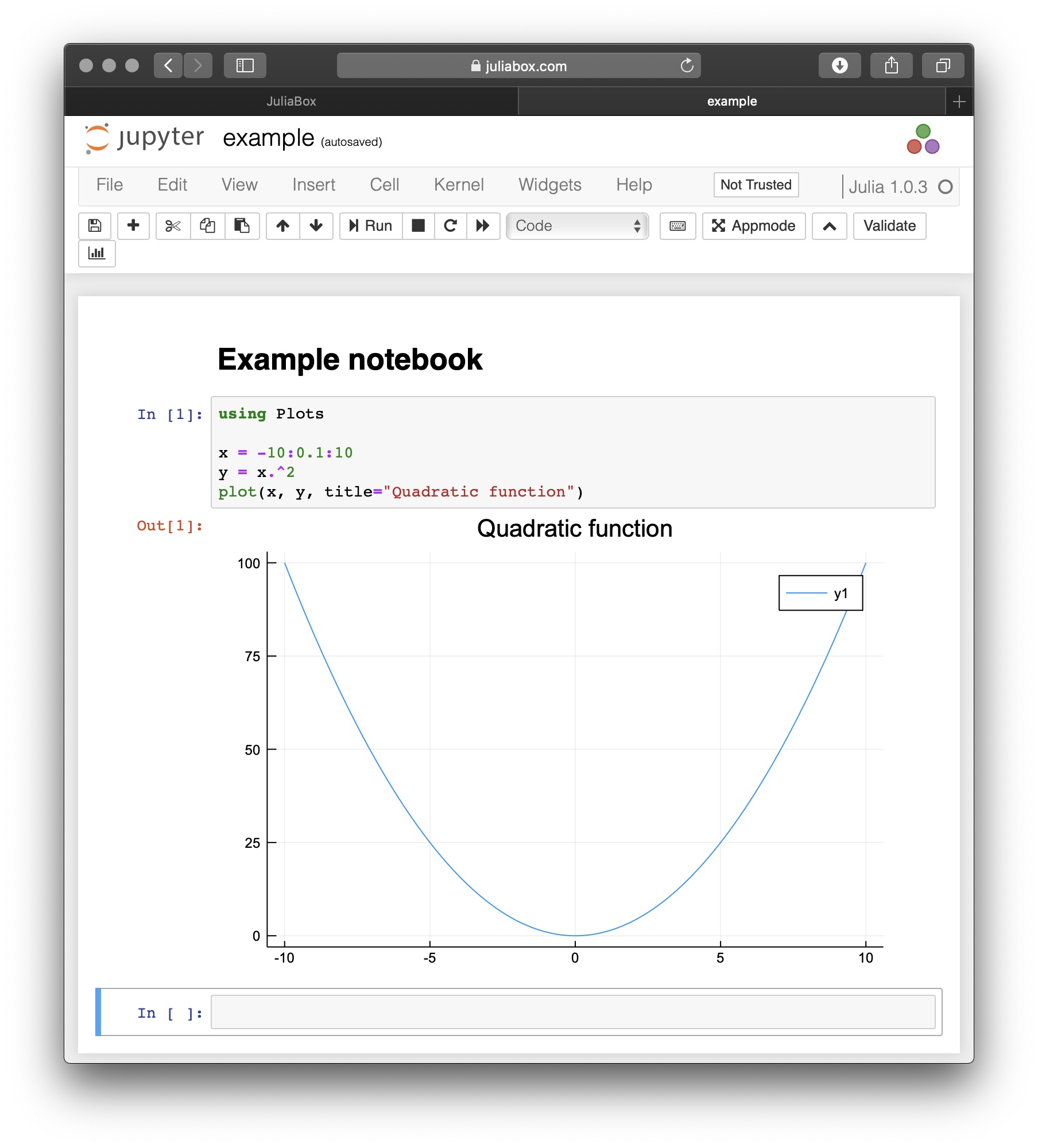
Apéndice C: Cambios de ThinkJulia
Este libro es una traducción de ThinkJulia, que está disponible bajo la Licencia Creative Commons Atribución-NoComercial 3.0 No portada. Esta licencia requiere que los trabajos derivados (como este libro) enumeren los cambios realizados en relación a la fuente.
Las diferencias de este libro respecto a ThinkJulia incluyen lo siguiente:
-
Traducción del inglés al español.
-
Se cambiaron muchas frases idiomáticas que no serían familiares para los hispanohablantes ("Se cayó el centavo").
-
En vez de usar el texto de la novela "Emma" en el Capítulo 13, se usa el texto de "Don Quijote".
-
Debido a que O’Reilly no financió la traducción, algunas de las referencias a O’Reilly en el prefacio fueron eliminadas.